第2讲 圆锥曲线的方程与性质——小题备考 课件(共35张PPT)
文档属性
| 名称 | 第2讲 圆锥曲线的方程与性质——小题备考 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 01:05:31 | ||
图片预览











文档简介
(共35张PPT)
第2讲 圆锥曲线的方程与性质——小题备考
微专题1 圆锥曲线的定义应用
微专题2 圆锥曲线的几何性质
微专题3 离心率的问题
微专题1
圆锥曲线的定义应用
『常考常用结论』
1.椭圆的定义与方程:|MF1|+|MF2|=2a(2a>|F1F2|);
焦点在x轴上:=1(a>b>0),
焦点在y轴上:=1(a>b>0).
2.双曲线的定义与方程:||MF1|-|MF2||=2a(2a<|F1F2|);
焦点在x轴上:=1(a>0,b>0),
焦点在y轴上:=1(a>0,b>0).
3.抛物线定义与方程:|MF|=d(d为M点到准线的距离)
y2=2px,y2=-2px,x2=2py,x2=-2py(p>0)
『保分题组训练』
1.已知F1,F2为椭圆=1的两个焦点,过F1的直线交椭圆于A,B两点,若|F2A|+|F2B|=10,则|AB|=( )
A.2 B.4
C.6 D.10
解析:由=1,可得a=4,
根据椭圆的定义|F1A|+|F2A|+|F1B|+|F2B|=4a=16,又|F2A|+|F2B|=10,
所以|AB|=|F1A|+|F1B|=6.
故选C.
C
2.[2021·河北石家庄二模]抛物线y=ax2经过点M(2,1),则M到焦点F的距离为( )
A. B. 2
C. 3 D.
解析:∵M(2,1)在抛物线y=ax2上,∴4a=1,解得:a=,
∴抛物线标准方程为x2=4y,∴F(0,1),∴|MF|=1+1=2.
故选B.
B
3.已知双曲线=1(0A. B.
C.1 D.2
解析:由题知a2=3-m,b2=m,所以c=,
因为|OP|=|F1F2|,所以PF1⊥PF2,
又∠PF1F2=30°,所以|PF1|=3,|PF2|=,
所以由双曲线的定义可知|PF1|-|PF2|=3-=2,解得m=.故选B.
B
『提分题组训练』
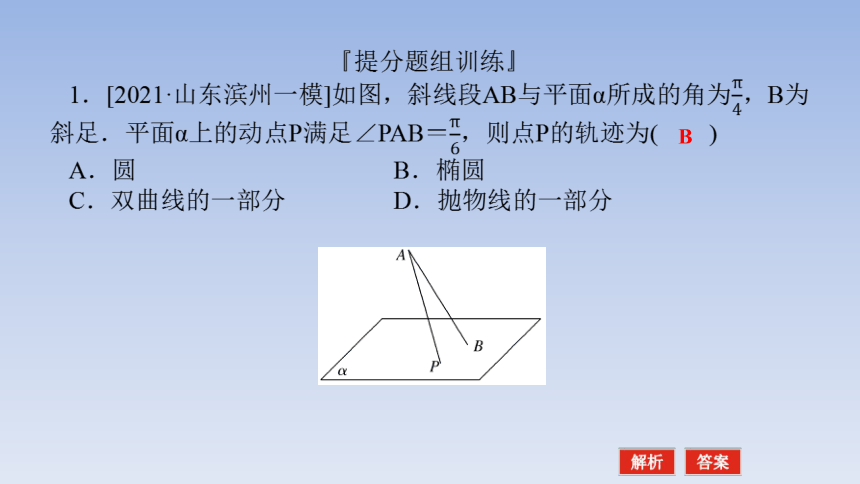
1.[2021·山东滨州一模]如图,斜线段AB与平面α所成的角为,B为斜足.平面α上的动点P满足∠PAB=,则点P的轨迹为( )
A.圆 B.椭圆
C.双曲线的一部分 D.抛物线的一部分
B
解析:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.参考图:此题中平面α上的动点P满足∠PAB=,
可理解为P在以AB为轴的圆锥的侧面上,再由斜线段AB与平面α所成的角为,可知P的轨迹符合圆锥曲线中椭圆定义,故可知动点P的轨迹是椭圆.故选B.
2.[2021·湖南永州模拟]已知F是抛物线y2=4x的焦点,若A,B是该抛物线上的两点,且|AF|+|BF|=6,则线段AB的中点到直线x=-的距离为( )
A.2 B. C. 3 D.
解析:∵F是抛物线y2=4x的焦点,F(1,0),准线方程x=-1,
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+1+x2+1=6,即x1+x2=4,
∴线段AB的中点横坐标为(x1+x2)=2,
∴线段AB的中点到直线x=-的距离为2+=.
故选B.
B
3.[2021·河北秦皇岛二模]已知双曲线C:x2-=1的左、右焦点分别为F1、F2,直线l过F2与双曲线C的左、右两支分别交于A、B两点,已知∠F1AF2=90°,且△ABF1内切圆半径为1,则|AB|=________.
解析:双曲线C:x2-=1的a=1,
设|AF1|=m,|BF1|=n,
由双曲线的定义可得|AF2|=|AF1|+2a=m+2,
|BF2|=|BF1|-2a=n-2,
|AB|=|AF2|-|BF2|=m-n+4,
由切线长定理可得直角三角形的内切圆的半径为两直角边的和与斜边的差的一半,
所以,在直角三角形ABF1中,(|AB|+|AF1|-|BF1|)=(m-n+4+m-n)=1,
可得m-n=-1,
所以|AB|=-1+4=3.
3
【技法领悟】
关于圆锥曲线定义的应用
对于椭圆、双曲线如果涉及曲线上的点与焦点的距离,一般要利用定义进行转化.对应抛物线涉及曲线上的点到焦点的距离、到准线的距离时需要相互转化.
微专题2
圆锥曲线的几何性质
『常考常用结论』
1.椭圆中,长轴是最长的弦,过焦点的所有弦长中,通径最短,通径长l=.距焦点最短的点是相应的对称轴同侧顶点.
2.双曲线=1(a>0,b>0)的渐近线方程为y=±x.
双曲线=1(a>0,b>0)的渐近线方程为y=±x.
3.抛物线y2=2px(p>0)的焦点F,准线方程x=-;
抛物线x2=2py(p>0)的焦点F,准线方程y=-.
『保分题组训练』
1.已知椭圆C:=1的离心率为,则椭圆C的长轴长为( )
A.2 B.4
C.4 D.8
解析:由题意知c2=m+4-m=4,所以c=2,
又因为=,所以m=8,
所以椭圆C的长轴长为2=4.
故选C.
C
2.若抛物线y2=2px的焦点与双曲线=1的右焦点重合,则p的值为( )
A.4 B.2
C. D.2
解析:抛物线y2=2px的焦点为,双曲线=1的右焦点为(2,0),
因为抛物线的焦点与双曲线的右焦点重合,
所以=2,p=4,
故选A.
A
3.[2021·湖南永州模拟]写出一个渐近线方程为y=±x的双曲线标准方程____________.
解析:不妨设双曲线方程焦点在x轴上,渐近线方程为y=±x,则=1.
x2-y2=1
『提分题组训练』
1.[2021·山东淄博一模]实轴长与焦距之比为黄金数的双曲线叫黄金双曲线.若双曲线=1(a>0,b>0)是黄金双曲线,则等于( )
A. B. C. D.
解析:由题意可知=,
∴=,
即==,
∴=,
∴=,
故选A.
A
2.已知椭圆C的方程是=1(a>b>0),点A在椭圆C上,过点A且斜率为-的直线恰好经过椭圆的一个焦点,则椭圆C的方程为( )
A.=1 B.=1 C.=1 D.=1
解析:过点A且斜率为-的直线方程为y-=-(x+1),由椭圆C的标准方程知其焦点在x轴上,令y=0,解得x=1,
可得椭圆的右焦点为F(1,0),则c=1,又A在椭圆C上,则=1,又a2=b2+1,
从而有4b4-9b2-9=0,解得b2=3或b2=-(舍去),则a2=4,
所以椭圆C的方程为=1.
故选D.
D
3.[2021·辽宁朝阳一模]抛物线C:y2=2px(p>0)的焦点为F,过F与x轴垂直的直线交C于点M,N,有下列四个命题:
甲:点F坐标为(1,0);
乙:抛物线C的准线方程为x=-2;
丙:线段MN长为4;
丁:直线y=x+1与抛物线C相切.
如果只有一个命题是假命题,则该命题是( )
A.甲 B.乙
C.丙 D.丁
B
解析:抛物线C:y2=2px(p>0)的焦点坐标为F,
若=1,则p=2,F(1,0),甲正确;
抛物线的准线方程为x=-1,乙错误;
抛物线的通径为2p=4,丙正确;
抛物线方程为y2=4x,与y=x+1联立,可得x2-2x+1=0,即x=1,
可得直线y=x+1与抛物线C相切于,丁正确.
若=2,则p=4,可得F,甲错误;
准线方程为x=-2,乙正确;
抛物线的通径为2p=8,丙错误,不合题意.
故p=2,甲、丙、丁正确,乙错误.
故选B.
【技法领悟】
1.理清圆锥曲线中a,b,c,e,p的关系是关键.
2.双曲线的渐近线方程:利用公式e=,建立离心率与渐近线斜率的关系,知道一个可以求另一个.
微专题3
离心率问题
『常考常用结论』
1.椭圆离心率e==.
2.双曲线离心率e==.
『保分题组训练』
1.[2021·山东青岛一模]已知双曲线=1(a>0,b>0)的一条渐近线的倾斜角为,则该双曲线的离心率为( )
A. B.
C. D.2
解析:双曲线焦点在y轴上,则双曲线的一条渐近线为y=x,由倾斜角为,得==,离心率e===.
故选C.
C
2.椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率为( )
A. B.
C. D.
C
解析:设椭圆E的短轴长为2b,长轴长为2a,焦距为2c,
则2b=6,即b=3;a+c=9或a-c=9,
若a+c=9,①
∵b2=a2-c2=(a+c)(a-c)=9(a-c)=32=9,
∴a-c=1,②
由①②得:a=5,c=4,∴椭圆E的离心率e=;
若a-c=9,③
∵b2=a2-c2=(a+c)(a-c)=9(a+c)=32=9,
∴a+c=1,④
由③④得:a=5,c=-4,不符合题意,舍去,
故椭圆E的离心率为.
故选C.
3.[2021·湖北五校联考]双曲线C:=1(a>0,b>0),圆M:(x+3)2+y2=4与双曲线C的一条渐近线相交所得弦长为2,则双曲线的离心率等于( )
A. B. C. D.
解析:由题意可知圆心(-3,0),半径为2,
又因为渐近线与圆相交所得弦长为2,
则圆心到渐近线的距离等于=,
双曲线的一条渐近线为ax-by=0,
运用点到直线的距离公式可得==,
所以c=a,故e==,
故选B.
B
4.[2021·河北保定二模]已知F1、F2是椭圆=1(a>b>0)的两个焦点,过F2的直线与椭圆交于A、B两点,若|AF1|∶|AB|∶|BF1|=3∶4∶5,则该椭圆的离心率为( )
A. B.2- C. D.
解析:如图所示,设|AF1|=3t,则|AB|=4t,|BF1|=5t,所以+|AB|2=|BF1|2,
所以,∠F1AF2=90°,
由椭圆定义可得|AF1|+|AB|+|BF1|=12t=4a,∴t=,∴|AF1|=3t=a,
所以,|AF2|=2a-|AF1|=a,
所以,△AF1F2为等腰直角三角形,可得|AF1|2+|AF2|2=|F1F2|2,∴2a2=4c2,
所以,该椭圆的离心率为e==.
故选D.
D
『提分题组训练』
1.已知椭圆C:=1(a>b>0),过椭圆左顶点,且斜率为的直线交椭圆C于另外一点B,椭圆右焦点为F,BF⊥x轴,则椭圆C的离心率为( )
A. B. C. D.
解析:因为BF⊥x轴,则B点的横坐标为c,且点B在椭圆上,代入椭圆方程=1,解得B点坐标,
又椭圆左顶点坐标为(-a,0),直线斜率为,所以有k==,即4b2=ac+a2,代入b2=a2-c2可得3a2-ac-4c2=0,即-3=0 解得=-1(舍)或=,则离心率为e=.
故选A.
A
2.[2021·湖南六校联考]已知F1,F2分别是双曲线=1(a>0,b>0)的左、右焦点,点P是该双曲线上一点且在第一象限内,2sin ∠PF1F2=sin ∠PF2F1,则双曲线的离心率的取值范围为( )
A.(1,2) B.(3,+∞) C.(1,3) D.(2,3)
解析:在△PF1F2中,由正弦定理知,=,
∵2sin ∠PF1F2=sin ∠PF2F1,
∴2|PF2|=|PF1|,
由双曲线的定义知,|PF1|-|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∵|PF1|+|PF2|>|F1F2|,即4a+2a>2c,
∴e=<3,
又e>1,∴e∈(1,3).
故选C.
C
3.[2021·河北秦皇岛二模]椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线l交椭圆C于A,B两点,已知==,则椭圆C的离心率为( )
A. B.
C. D.
A
解析:设|F1F2|=2c,
因为·=·==0
所以|AF2|=|F1F2|=2c,所以|AF1|=2a-2c,
因为=,所以|BF1|=(a-c),所以|BF2|=,
设AF1的中点为H,则F2H⊥AB,|AH|=a-c,|BH|=(a-c),
|F2A|2-|AH|2=|F2B|2-|BH|2,即4c2-(a-c)2=-(a-c)2,
整理可得7c2-12ac+5a2=0,即7e2-12e+5=0,
解得e=或1(舍去),所以离心率为,
故选A.
4.[2021·广东大联考]已知F1,F2是双曲线=1(a>0,b>0)的左、右焦点,点M为双曲线的左支上一点,满足|MF1|=2|F1F2|,且cos ∠MF1F2=-,则该双曲线的离心率e=________.
解析:由已知可设|F1F2|=2c,
又点M为双曲线的左支上一点,满足|MF1|=2|F1F2|,则|MF2|-|MF1|=2a,
且|MF1|=4c,所以|MF2|=2a+4c,
在三角形MF1F2中,由余弦定理可得:cos ∠MF1F2=
==-,整理可得9c2-16ac-4a2=0,
即9e2-16e-4=0,解得e=2或-(舍去),
所以双曲线的离心率为2.
2
【技法领悟】
根据条件建立关于a,b,c之间的方程,结合其自身的关系消元,构造方程求离心率.
第2讲 圆锥曲线的方程与性质——小题备考
微专题1 圆锥曲线的定义应用
微专题2 圆锥曲线的几何性质
微专题3 离心率的问题
微专题1
圆锥曲线的定义应用
『常考常用结论』
1.椭圆的定义与方程:|MF1|+|MF2|=2a(2a>|F1F2|);
焦点在x轴上:=1(a>b>0),
焦点在y轴上:=1(a>b>0).
2.双曲线的定义与方程:||MF1|-|MF2||=2a(2a<|F1F2|);
焦点在x轴上:=1(a>0,b>0),
焦点在y轴上:=1(a>0,b>0).
3.抛物线定义与方程:|MF|=d(d为M点到准线的距离)
y2=2px,y2=-2px,x2=2py,x2=-2py(p>0)
『保分题组训练』
1.已知F1,F2为椭圆=1的两个焦点,过F1的直线交椭圆于A,B两点,若|F2A|+|F2B|=10,则|AB|=( )
A.2 B.4
C.6 D.10
解析:由=1,可得a=4,
根据椭圆的定义|F1A|+|F2A|+|F1B|+|F2B|=4a=16,又|F2A|+|F2B|=10,
所以|AB|=|F1A|+|F1B|=6.
故选C.
C
2.[2021·河北石家庄二模]抛物线y=ax2经过点M(2,1),则M到焦点F的距离为( )
A. B. 2
C. 3 D.
解析:∵M(2,1)在抛物线y=ax2上,∴4a=1,解得:a=,
∴抛物线标准方程为x2=4y,∴F(0,1),∴|MF|=1+1=2.
故选B.
B
3.已知双曲线=1(0
C.1 D.2
解析:由题知a2=3-m,b2=m,所以c=,
因为|OP|=|F1F2|,所以PF1⊥PF2,
又∠PF1F2=30°,所以|PF1|=3,|PF2|=,
所以由双曲线的定义可知|PF1|-|PF2|=3-=2,解得m=.故选B.
B
『提分题组训练』
1.[2021·山东滨州一模]如图,斜线段AB与平面α所成的角为,B为斜足.平面α上的动点P满足∠PAB=,则点P的轨迹为( )
A.圆 B.椭圆
C.双曲线的一部分 D.抛物线的一部分
B
解析:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.参考图:此题中平面α上的动点P满足∠PAB=,
可理解为P在以AB为轴的圆锥的侧面上,再由斜线段AB与平面α所成的角为,可知P的轨迹符合圆锥曲线中椭圆定义,故可知动点P的轨迹是椭圆.故选B.
2.[2021·湖南永州模拟]已知F是抛物线y2=4x的焦点,若A,B是该抛物线上的两点,且|AF|+|BF|=6,则线段AB的中点到直线x=-的距离为( )
A.2 B. C. 3 D.
解析:∵F是抛物线y2=4x的焦点,F(1,0),准线方程x=-1,
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+1+x2+1=6,即x1+x2=4,
∴线段AB的中点横坐标为(x1+x2)=2,
∴线段AB的中点到直线x=-的距离为2+=.
故选B.
B
3.[2021·河北秦皇岛二模]已知双曲线C:x2-=1的左、右焦点分别为F1、F2,直线l过F2与双曲线C的左、右两支分别交于A、B两点,已知∠F1AF2=90°,且△ABF1内切圆半径为1,则|AB|=________.
解析:双曲线C:x2-=1的a=1,
设|AF1|=m,|BF1|=n,
由双曲线的定义可得|AF2|=|AF1|+2a=m+2,
|BF2|=|BF1|-2a=n-2,
|AB|=|AF2|-|BF2|=m-n+4,
由切线长定理可得直角三角形的内切圆的半径为两直角边的和与斜边的差的一半,
所以,在直角三角形ABF1中,(|AB|+|AF1|-|BF1|)=(m-n+4+m-n)=1,
可得m-n=-1,
所以|AB|=-1+4=3.
3
【技法领悟】
关于圆锥曲线定义的应用
对于椭圆、双曲线如果涉及曲线上的点与焦点的距离,一般要利用定义进行转化.对应抛物线涉及曲线上的点到焦点的距离、到准线的距离时需要相互转化.
微专题2
圆锥曲线的几何性质
『常考常用结论』
1.椭圆中,长轴是最长的弦,过焦点的所有弦长中,通径最短,通径长l=.距焦点最短的点是相应的对称轴同侧顶点.
2.双曲线=1(a>0,b>0)的渐近线方程为y=±x.
双曲线=1(a>0,b>0)的渐近线方程为y=±x.
3.抛物线y2=2px(p>0)的焦点F,准线方程x=-;
抛物线x2=2py(p>0)的焦点F,准线方程y=-.
『保分题组训练』
1.已知椭圆C:=1的离心率为,则椭圆C的长轴长为( )
A.2 B.4
C.4 D.8
解析:由题意知c2=m+4-m=4,所以c=2,
又因为=,所以m=8,
所以椭圆C的长轴长为2=4.
故选C.
C
2.若抛物线y2=2px的焦点与双曲线=1的右焦点重合,则p的值为( )
A.4 B.2
C. D.2
解析:抛物线y2=2px的焦点为,双曲线=1的右焦点为(2,0),
因为抛物线的焦点与双曲线的右焦点重合,
所以=2,p=4,
故选A.
A
3.[2021·湖南永州模拟]写出一个渐近线方程为y=±x的双曲线标准方程____________.
解析:不妨设双曲线方程焦点在x轴上,渐近线方程为y=±x,则=1.
x2-y2=1
『提分题组训练』
1.[2021·山东淄博一模]实轴长与焦距之比为黄金数的双曲线叫黄金双曲线.若双曲线=1(a>0,b>0)是黄金双曲线,则等于( )
A. B. C. D.
解析:由题意可知=,
∴=,
即==,
∴=,
∴=,
故选A.
A
2.已知椭圆C的方程是=1(a>b>0),点A在椭圆C上,过点A且斜率为-的直线恰好经过椭圆的一个焦点,则椭圆C的方程为( )
A.=1 B.=1 C.=1 D.=1
解析:过点A且斜率为-的直线方程为y-=-(x+1),由椭圆C的标准方程知其焦点在x轴上,令y=0,解得x=1,
可得椭圆的右焦点为F(1,0),则c=1,又A在椭圆C上,则=1,又a2=b2+1,
从而有4b4-9b2-9=0,解得b2=3或b2=-(舍去),则a2=4,
所以椭圆C的方程为=1.
故选D.
D
3.[2021·辽宁朝阳一模]抛物线C:y2=2px(p>0)的焦点为F,过F与x轴垂直的直线交C于点M,N,有下列四个命题:
甲:点F坐标为(1,0);
乙:抛物线C的准线方程为x=-2;
丙:线段MN长为4;
丁:直线y=x+1与抛物线C相切.
如果只有一个命题是假命题,则该命题是( )
A.甲 B.乙
C.丙 D.丁
B
解析:抛物线C:y2=2px(p>0)的焦点坐标为F,
若=1,则p=2,F(1,0),甲正确;
抛物线的准线方程为x=-1,乙错误;
抛物线的通径为2p=4,丙正确;
抛物线方程为y2=4x,与y=x+1联立,可得x2-2x+1=0,即x=1,
可得直线y=x+1与抛物线C相切于,丁正确.
若=2,则p=4,可得F,甲错误;
准线方程为x=-2,乙正确;
抛物线的通径为2p=8,丙错误,不合题意.
故p=2,甲、丙、丁正确,乙错误.
故选B.
【技法领悟】
1.理清圆锥曲线中a,b,c,e,p的关系是关键.
2.双曲线的渐近线方程:利用公式e=,建立离心率与渐近线斜率的关系,知道一个可以求另一个.
微专题3
离心率问题
『常考常用结论』
1.椭圆离心率e==.
2.双曲线离心率e==.
『保分题组训练』
1.[2021·山东青岛一模]已知双曲线=1(a>0,b>0)的一条渐近线的倾斜角为,则该双曲线的离心率为( )
A. B.
C. D.2
解析:双曲线焦点在y轴上,则双曲线的一条渐近线为y=x,由倾斜角为,得==,离心率e===.
故选C.
C
2.椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率为( )
A. B.
C. D.
C
解析:设椭圆E的短轴长为2b,长轴长为2a,焦距为2c,
则2b=6,即b=3;a+c=9或a-c=9,
若a+c=9,①
∵b2=a2-c2=(a+c)(a-c)=9(a-c)=32=9,
∴a-c=1,②
由①②得:a=5,c=4,∴椭圆E的离心率e=;
若a-c=9,③
∵b2=a2-c2=(a+c)(a-c)=9(a+c)=32=9,
∴a+c=1,④
由③④得:a=5,c=-4,不符合题意,舍去,
故椭圆E的离心率为.
故选C.
3.[2021·湖北五校联考]双曲线C:=1(a>0,b>0),圆M:(x+3)2+y2=4与双曲线C的一条渐近线相交所得弦长为2,则双曲线的离心率等于( )
A. B. C. D.
解析:由题意可知圆心(-3,0),半径为2,
又因为渐近线与圆相交所得弦长为2,
则圆心到渐近线的距离等于=,
双曲线的一条渐近线为ax-by=0,
运用点到直线的距离公式可得==,
所以c=a,故e==,
故选B.
B
4.[2021·河北保定二模]已知F1、F2是椭圆=1(a>b>0)的两个焦点,过F2的直线与椭圆交于A、B两点,若|AF1|∶|AB|∶|BF1|=3∶4∶5,则该椭圆的离心率为( )
A. B.2- C. D.
解析:如图所示,设|AF1|=3t,则|AB|=4t,|BF1|=5t,所以+|AB|2=|BF1|2,
所以,∠F1AF2=90°,
由椭圆定义可得|AF1|+|AB|+|BF1|=12t=4a,∴t=,∴|AF1|=3t=a,
所以,|AF2|=2a-|AF1|=a,
所以,△AF1F2为等腰直角三角形,可得|AF1|2+|AF2|2=|F1F2|2,∴2a2=4c2,
所以,该椭圆的离心率为e==.
故选D.
D
『提分题组训练』
1.已知椭圆C:=1(a>b>0),过椭圆左顶点,且斜率为的直线交椭圆C于另外一点B,椭圆右焦点为F,BF⊥x轴,则椭圆C的离心率为( )
A. B. C. D.
解析:因为BF⊥x轴,则B点的横坐标为c,且点B在椭圆上,代入椭圆方程=1,解得B点坐标,
又椭圆左顶点坐标为(-a,0),直线斜率为,所以有k==,即4b2=ac+a2,代入b2=a2-c2可得3a2-ac-4c2=0,即-3=0 解得=-1(舍)或=,则离心率为e=.
故选A.
A
2.[2021·湖南六校联考]已知F1,F2分别是双曲线=1(a>0,b>0)的左、右焦点,点P是该双曲线上一点且在第一象限内,2sin ∠PF1F2=sin ∠PF2F1,则双曲线的离心率的取值范围为( )
A.(1,2) B.(3,+∞) C.(1,3) D.(2,3)
解析:在△PF1F2中,由正弦定理知,=,
∵2sin ∠PF1F2=sin ∠PF2F1,
∴2|PF2|=|PF1|,
由双曲线的定义知,|PF1|-|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∵|PF1|+|PF2|>|F1F2|,即4a+2a>2c,
∴e=<3,
又e>1,∴e∈(1,3).
故选C.
C
3.[2021·河北秦皇岛二模]椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线l交椭圆C于A,B两点,已知==,则椭圆C的离心率为( )
A. B.
C. D.
A
解析:设|F1F2|=2c,
因为·=·==0
所以|AF2|=|F1F2|=2c,所以|AF1|=2a-2c,
因为=,所以|BF1|=(a-c),所以|BF2|=,
设AF1的中点为H,则F2H⊥AB,|AH|=a-c,|BH|=(a-c),
|F2A|2-|AH|2=|F2B|2-|BH|2,即4c2-(a-c)2=-(a-c)2,
整理可得7c2-12ac+5a2=0,即7e2-12e+5=0,
解得e=或1(舍去),所以离心率为,
故选A.
4.[2021·广东大联考]已知F1,F2是双曲线=1(a>0,b>0)的左、右焦点,点M为双曲线的左支上一点,满足|MF1|=2|F1F2|,且cos ∠MF1F2=-,则该双曲线的离心率e=________.
解析:由已知可设|F1F2|=2c,
又点M为双曲线的左支上一点,满足|MF1|=2|F1F2|,则|MF2|-|MF1|=2a,
且|MF1|=4c,所以|MF2|=2a+4c,
在三角形MF1F2中,由余弦定理可得:cos ∠MF1F2=
==-,整理可得9c2-16ac-4a2=0,
即9e2-16e-4=0,解得e=2或-(舍去),
所以双曲线的离心率为2.
2
【技法领悟】
根据条件建立关于a,b,c之间的方程,结合其自身的关系消元,构造方程求离心率.
同课章节目录
