第4讲 圆锥曲线中的最值、范围问题——大题备考 课件(共26张PPT)
文档属性
| 名称 | 第4讲 圆锥曲线中的最值、范围问题——大题备考 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 01:06:13 | ||
图片预览




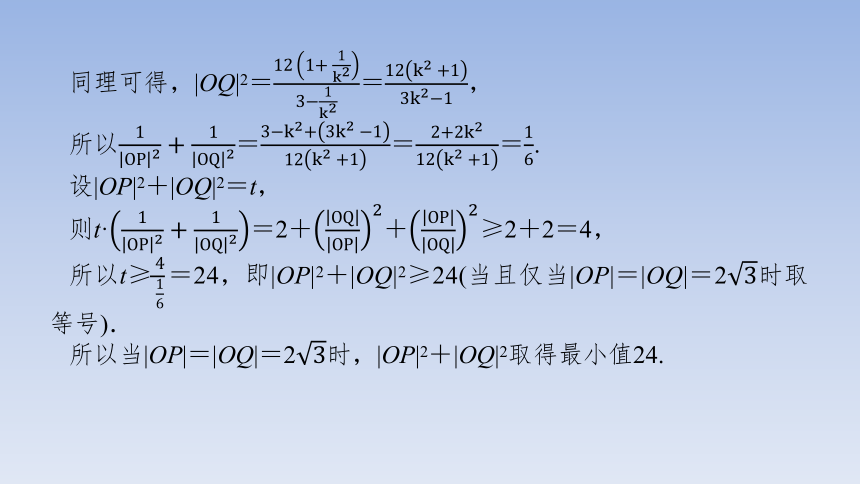

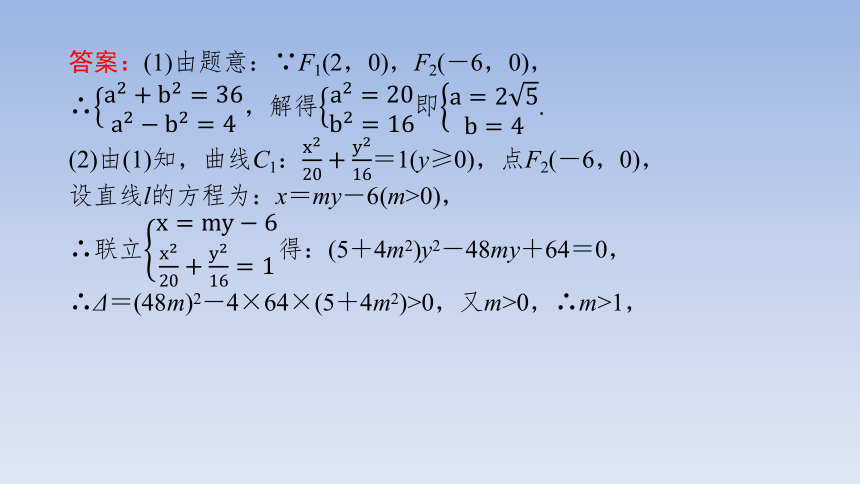
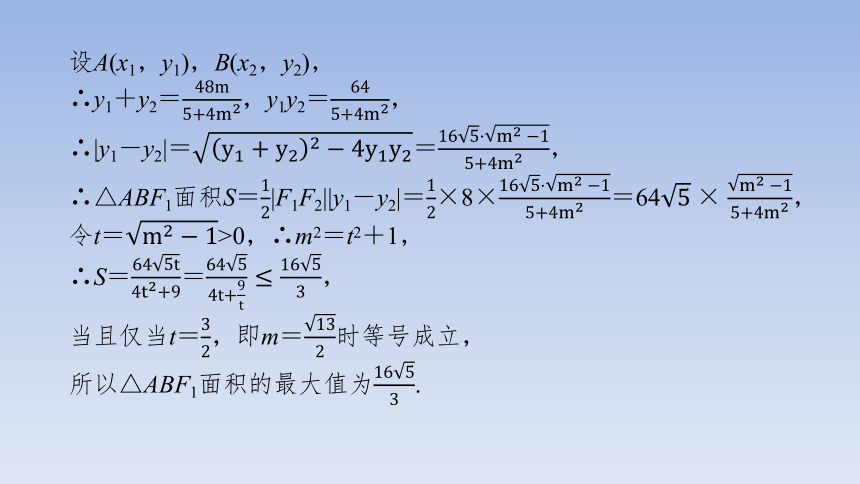
文档简介
(共26张PPT)
第4讲 圆锥曲线中的最值、范围问题——大题备考
微专题1 圆锥曲线中的最值问题
微专题2 圆锥曲线中的范围问题
微专题1
圆锥曲线中的最值问题
『抢分题组训练』
1.已知双曲线=1(a>0,b>0),O为坐标原点,离心率e=2,点M在双曲线上.
(1)求双曲线的方程;
(2)如图,若直线l与双曲线的左、右两支分别交于点Q,P,且·=0,求|OP|2+|OQ|2的最小值.
答案:(1)因为e==2,所以c=2a,b2=c2-a2=3a2.
所以双曲线的方程为=1,即3x2-y2=3a2.
因为点M()在双曲线上,所以15-3=3a2,所以a2=4.
所以所求双曲线的方程为=1.
(2)由·=0,得OP⊥OQ.设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=-x,
由,得,
所以|OP|2=x2+y2=.
同理可得,|OQ|2==,
所以===.
设|OP|2+|OQ|2=t,
则t·=2++≥2+2=4,
所以t≥=24,即|OP|2+|OQ|2≥24(当且仅当|OP|=|OQ|=2时取等号).
所以当|OP|=|OQ|=2时,|OP|2+|OQ|2取得最小值24.
2.[2021·福建龙岩模拟]已知a>b>0,曲线Γ由曲线C1:=1(y≥0)和曲线C2:=1(y<0)组成,其中曲线C1的右焦点为F1(2,0),曲线C2的左焦点F2(-6,0).
(1)求a,b的值;
(2)若直线l过点F2交曲线C1于点A,B,求△ABF1面积的最大值.
答案:(1)由题意:∵F1(2,0),F2(-6,0),
∴,解得即.
(2)由(1)知,曲线C1:=1(y≥0),点F2(-6,0),
设直线l的方程为:x=my-6(m>0),
∴联立得:(5+4m2)y2-48my+64=0,
∴Δ=(48m)2-4×64×(5+4m2)>0,又m>0,∴m>1,
设A(x1,y1),B(x2,y2),
∴y1+y2=,y1y2=,
∴|y1-y2|==,
∴△ABF1面积S=|F1F2||y1-y2|=×8×=64,
令t=>0,∴m2=t2+1,
∴S==,
当且仅当t=,即m=时等号成立,
所以△ABF1面积的最大值为.
3.[2021·全国乙卷]已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2.
(1)求C的方程;
(2)已知O为坐标原点,点P在C上,点Q满足=9,求直线OQ斜率的最大值.
答案:(1)由抛物线的定义可知,焦点F到准线的距离为p,故p=2,所以C的方程为y2=4x.
(2)由(1)知F(1,0),设P(x1,y1),Q(x2,y2),
则=(x2-x1,y2-y1),=(1-x2,-y2),
因为=9 ,所以,
可得,
又点P在抛物线C上,所以=4x1,即(10y2)2=4(10x2-9),化简得=x2-,则点Q的轨迹方程为y2=x-.
设直线OQ的方程为y=kx,易知当直线OQ与曲线y2=x-相切时,斜率可以取最大,
联立y=kx与y2=x-并化简,得k2x2-x+=0,
令Δ=(-)2-4k2·=0,解得k=±,
所以直线OQ斜率的最大值为.
【技法领悟】
解圆锥曲线中最值问题的解题模型
微专题2
圆锥曲线中的范围问题
『抢分题组训练』
1.已知抛物线C:y2=2px(p>0)的焦点为F,点M在第一象限且为抛物线C上一点,点N(5,0)在点F右侧,且△MNF恰为等边三角形.
(1)求C的方程;
(2)若直线l:x=ky+m与C交于A,B两点,∠AOB=120°(其中O为坐标原点),求实数m的取值范围.
答案:(1)由题意知:xM==,|NF|=5-,
由抛物线的定义知:|MF|=xM+,由|NF|=|MF|,得p=2,
∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),由,得y2-4ky-4m=0,Δ=16k2+16m>0,
∴,而x1+x2=k(y1+y2)+2m=4k2+2m,x1x2==m2,
又∠AOB=120°,即cos ∠AOB=====-,
∴m2-4m<0且4(m-4)2=m2+16k2+8m+16,
∴,得02.[2021·湖北高三二模]过双曲线Γ:=1(a>0,b>0)左焦点F1的动直线l与Γ的左支交于A,B两点,设Γ的右焦点为F2.
(1)若三角形ABF2可以是边长为4的正三角形,求此时Γ的标准方程;
(2)若存在直线l,使得AF2⊥BF2,求Γ离心率的取值范围.
答案:(1)依题意得:
|AF1|=2,|AF2|=4,|F1F2|=2.∴2a=|AF2|-|AF1|=2,a=1,
2c=|F1F2|=2,c=,b2=c2-a2=2,
此时Γ的方程为x2-=1.
(2)设l的方程为x=my-c,与=1联立,得(b2m2-a2)y2-2b2cmy+b4=0.
设A(x1,y1),B(x2,y2),则y1+y2=,y1y2=,由AF2⊥BF2,·=0,(x1-c)(x2-c)+y1y2=0,
(my1-2c)(my2-2c)+y1y2=0 (m2+1)b4-4m2c2b2+4c2(b2m2-a2)=0
(m2+1)b4=4a2c2 (m2+1)=≥1 4a2c2≥(c2-a2)2,
∴c4+a4-6a2c2≤0 e4-6e2+1≤0,
又∵e>1,∴1∴1又A、B在左支且l过F1,
∴y1y2<0,<0 m2< m2+1=<+1.
∴4a25.
综上所述3.[2021·山东临沂二模]已知椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,点P在椭圆C上,以PF1为直径的圆E:x2+2=过焦点F2.
(1)求椭圆C的方程;
(2)若椭圆C的右顶点为A,与x轴不垂直的直线l交椭圆C于M,N两点(M,N与A点不重合),且满足AM⊥AN,点Q为MN中点,求直线MN与AQ的斜率之积的取值范围.
答案:(1)在圆E的方程中,令y=0,得x2=3,解得x=±,所以,F1,F2的坐标分别为(-,0),(,0).
∵E,又因为OE=F2P,OE∥F2P,所以点P的坐标为,
所以,2a=|PF1|+|PF2|=2×=4,得a=2,b=1,
即椭圆C的方程为+y2=1.
(2)右顶点为A(2,0),由题意可知直线AM的斜率存在且不为0,
设直线AM的方程为y=k(x-2),由MN与x轴不垂直,故k≠±1.
由得:(1+4k2)x2-16k2x+16k2-4=0,
设M(x1,y1),N(x2,y2),又点A(2,0),
则由根与系数的关系可得:2x1=,得x1=,y1=k(x1-2)=,
∵AM⊥AN,∴直线AN的方程为y=-(x-2),
用-替换k可得:x2=,y2=,
∴点Q坐标为,
∴直线AQ的斜率k1==,
直线MN的斜率k2===,
∴k1k2==,
∵k2>0且k2≠1,∴2k2++1>2=4,
∴0<<.即k1k2∈.
∴直线MN与AQ的斜率之积的取值范围是.
【技法领悟】
范围问题的解题策略
解决有关范围问题时,先要恰当地引入变量(如点的坐标、角、斜率等),寻找不等关系,其方法有:
1.利用判别式或几何性质来构造不等式,从而确定所求范围;
2.利用已知参数的取值范围,求新参数的范围,解此类问题的核心是在两个参数之间建立相等关系;
3.利用隐含的不等关系建立不等式,从而求出所求范围;
4.利用已知不等关系构造不等式,从而求出所求范围;
5.利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定所求范围;
6.利用已知,将条件转化为n个不等关系,从而求出参数的范围.
第4讲 圆锥曲线中的最值、范围问题——大题备考
微专题1 圆锥曲线中的最值问题
微专题2 圆锥曲线中的范围问题
微专题1
圆锥曲线中的最值问题
『抢分题组训练』
1.已知双曲线=1(a>0,b>0),O为坐标原点,离心率e=2,点M在双曲线上.
(1)求双曲线的方程;
(2)如图,若直线l与双曲线的左、右两支分别交于点Q,P,且·=0,求|OP|2+|OQ|2的最小值.
答案:(1)因为e==2,所以c=2a,b2=c2-a2=3a2.
所以双曲线的方程为=1,即3x2-y2=3a2.
因为点M()在双曲线上,所以15-3=3a2,所以a2=4.
所以所求双曲线的方程为=1.
(2)由·=0,得OP⊥OQ.设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=-x,
由,得,
所以|OP|2=x2+y2=.
同理可得,|OQ|2==,
所以===.
设|OP|2+|OQ|2=t,
则t·=2++≥2+2=4,
所以t≥=24,即|OP|2+|OQ|2≥24(当且仅当|OP|=|OQ|=2时取等号).
所以当|OP|=|OQ|=2时,|OP|2+|OQ|2取得最小值24.
2.[2021·福建龙岩模拟]已知a>b>0,曲线Γ由曲线C1:=1(y≥0)和曲线C2:=1(y<0)组成,其中曲线C1的右焦点为F1(2,0),曲线C2的左焦点F2(-6,0).
(1)求a,b的值;
(2)若直线l过点F2交曲线C1于点A,B,求△ABF1面积的最大值.
答案:(1)由题意:∵F1(2,0),F2(-6,0),
∴,解得即.
(2)由(1)知,曲线C1:=1(y≥0),点F2(-6,0),
设直线l的方程为:x=my-6(m>0),
∴联立得:(5+4m2)y2-48my+64=0,
∴Δ=(48m)2-4×64×(5+4m2)>0,又m>0,∴m>1,
设A(x1,y1),B(x2,y2),
∴y1+y2=,y1y2=,
∴|y1-y2|==,
∴△ABF1面积S=|F1F2||y1-y2|=×8×=64,
令t=>0,∴m2=t2+1,
∴S==,
当且仅当t=,即m=时等号成立,
所以△ABF1面积的最大值为.
3.[2021·全国乙卷]已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2.
(1)求C的方程;
(2)已知O为坐标原点,点P在C上,点Q满足=9,求直线OQ斜率的最大值.
答案:(1)由抛物线的定义可知,焦点F到准线的距离为p,故p=2,所以C的方程为y2=4x.
(2)由(1)知F(1,0),设P(x1,y1),Q(x2,y2),
则=(x2-x1,y2-y1),=(1-x2,-y2),
因为=9 ,所以,
可得,
又点P在抛物线C上,所以=4x1,即(10y2)2=4(10x2-9),化简得=x2-,则点Q的轨迹方程为y2=x-.
设直线OQ的方程为y=kx,易知当直线OQ与曲线y2=x-相切时,斜率可以取最大,
联立y=kx与y2=x-并化简,得k2x2-x+=0,
令Δ=(-)2-4k2·=0,解得k=±,
所以直线OQ斜率的最大值为.
【技法领悟】
解圆锥曲线中最值问题的解题模型
微专题2
圆锥曲线中的范围问题
『抢分题组训练』
1.已知抛物线C:y2=2px(p>0)的焦点为F,点M在第一象限且为抛物线C上一点,点N(5,0)在点F右侧,且△MNF恰为等边三角形.
(1)求C的方程;
(2)若直线l:x=ky+m与C交于A,B两点,∠AOB=120°(其中O为坐标原点),求实数m的取值范围.
答案:(1)由题意知:xM==,|NF|=5-,
由抛物线的定义知:|MF|=xM+,由|NF|=|MF|,得p=2,
∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),由,得y2-4ky-4m=0,Δ=16k2+16m>0,
∴,而x1+x2=k(y1+y2)+2m=4k2+2m,x1x2==m2,
又∠AOB=120°,即cos ∠AOB=====-,
∴m2-4m<0且4(m-4)2=m2+16k2+8m+16,
∴,得0
(1)若三角形ABF2可以是边长为4的正三角形,求此时Γ的标准方程;
(2)若存在直线l,使得AF2⊥BF2,求Γ离心率的取值范围.
答案:(1)依题意得:
|AF1|=2,|AF2|=4,|F1F2|=2.∴2a=|AF2|-|AF1|=2,a=1,
2c=|F1F2|=2,c=,b2=c2-a2=2,
此时Γ的方程为x2-=1.
(2)设l的方程为x=my-c,与=1联立,得(b2m2-a2)y2-2b2cmy+b4=0.
设A(x1,y1),B(x2,y2),则y1+y2=,y1y2=,由AF2⊥BF2,·=0,(x1-c)(x2-c)+y1y2=0,
(my1-2c)(my2-2c)+y1y2=0 (m2+1)b4-4m2c2b2+4c2(b2m2-a2)=0
(m2+1)b4=4a2c2 (m2+1)=≥1 4a2c2≥(c2-a2)2,
∴c4+a4-6a2c2≤0 e4-6e2+1≤0,
又∵e>1,∴1
∴y1y2<0,<0 m2< m2+1=<+1.
∴4a2
综上所述
(1)求椭圆C的方程;
(2)若椭圆C的右顶点为A,与x轴不垂直的直线l交椭圆C于M,N两点(M,N与A点不重合),且满足AM⊥AN,点Q为MN中点,求直线MN与AQ的斜率之积的取值范围.
答案:(1)在圆E的方程中,令y=0,得x2=3,解得x=±,所以,F1,F2的坐标分别为(-,0),(,0).
∵E,又因为OE=F2P,OE∥F2P,所以点P的坐标为,
所以,2a=|PF1|+|PF2|=2×=4,得a=2,b=1,
即椭圆C的方程为+y2=1.
(2)右顶点为A(2,0),由题意可知直线AM的斜率存在且不为0,
设直线AM的方程为y=k(x-2),由MN与x轴不垂直,故k≠±1.
由得:(1+4k2)x2-16k2x+16k2-4=0,
设M(x1,y1),N(x2,y2),又点A(2,0),
则由根与系数的关系可得:2x1=,得x1=,y1=k(x1-2)=,
∵AM⊥AN,∴直线AN的方程为y=-(x-2),
用-替换k可得:x2=,y2=,
∴点Q坐标为,
∴直线AQ的斜率k1==,
直线MN的斜率k2===,
∴k1k2==,
∵k2>0且k2≠1,∴2k2++1>2=4,
∴0<<.即k1k2∈.
∴直线MN与AQ的斜率之积的取值范围是.
【技法领悟】
范围问题的解题策略
解决有关范围问题时,先要恰当地引入变量(如点的坐标、角、斜率等),寻找不等关系,其方法有:
1.利用判别式或几何性质来构造不等式,从而确定所求范围;
2.利用已知参数的取值范围,求新参数的范围,解此类问题的核心是在两个参数之间建立相等关系;
3.利用隐含的不等关系建立不等式,从而求出所求范围;
4.利用已知不等关系构造不等式,从而求出所求范围;
5.利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定所求范围;
6.利用已知,将条件转化为n个不等关系,从而求出参数的范围.
同课章节目录
