第2讲 基本初等函数、函数与方程——小题备考 课件(共30张PPT)
文档属性
| 名称 | 第2讲 基本初等函数、函数与方程——小题备考 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 01:08:30 | ||
图片预览











文档简介
(共30张PPT)
第2讲 基本初等函数、函数与方程——小题备考
微专题1 基本初等函数的图象与性质
微专题2 函数零点与方程
微专题3 函数的实际应用
微专题1
基本初等函数的图象与性质
『常考常用结论』
1.指数与对数式的七个运算公式
(1)am·an=am+n;
(2)(am)n=amn;
(3)loga(MN)=logaM+logaN;
(4)loga=logaM-logaN;
(5)logaMn=nlogaM;
(6)alogaN=N;
(7)logaN=.
注:a>0且a≠1,b>0且b≠1,M>0,N>0.
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分01两种情况,当a>1时,两函数在定义域内都为增函数,当0『保分题组训练』
1.[2021·山东省实验中学二模]设a=50.3,b=log0.30.5,c=log30.4,则a,b,c的大小关系是( )
A.aC.c答案:D
解析:由a=50.3>1>b=log0.30.5>0>c=log30.4,
∴c2.函数f(x)=-loga(x-b)及g(x)=bx+a,则y=f(x)及y=g(x)的图象可能为( )
答案:B
解析:当00单调递减,f(t)=logat单调递减,所以f(x)=loga单调递增且定义域为(b,+∞),此时g(x)=bx+a与y轴的截距在(0,1)上,排除C.
当a>1时,t=>0单调递减,f(t)=logat单调递增,所以f(x)=loga单调递减且定义域为(b,+∞),此时g(x)=bx+a与y轴的截距在(1,+∞)上.
∴当b>0时,g(x)单调递增;当b<0时,g(x)单调递减,故只有B符合要求.
故选B.
3.已知函数f(x)=ex-e-x-( )
A.是偶函数,且在(-∞,0)上单调递增
B.是奇函数,且在(-∞,0)上单调递减
C.是偶函数,且在(-∞,0)上单调递减
D.是奇函数,且在(-∞,0)上单调递增
答案:D
解析:因为f(x)=ex-e-x-,x∈(-∞,0)
所以f(-x)=e-x-ex+=-f(x),即函数为奇函数,
当x<0时,f(x)=ex-e-x-单调递增,
故选D.
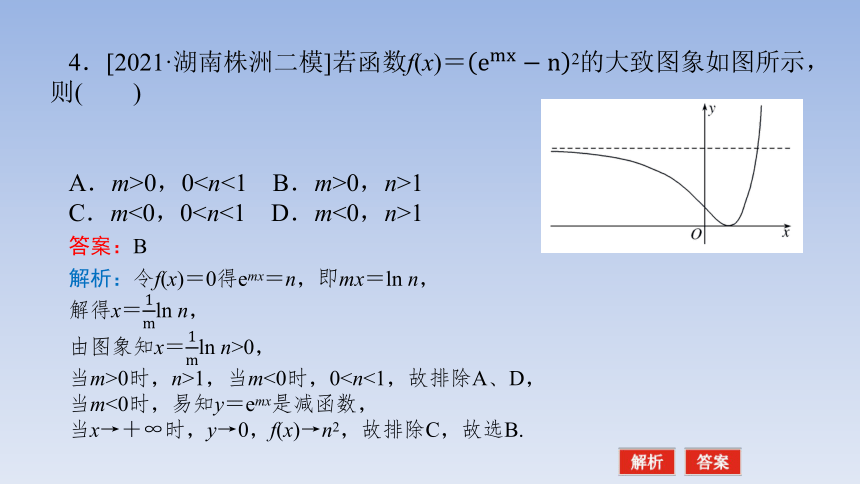
4.[2021·湖南株洲二模]若函数f(x)=2的大致图象如图所示,则( )
A.m>0,00,n>1
C.m<0,01
答案:B
解析:令f(x)=0得emx=n,即mx=ln n,
解得x=ln n,
由图象知x=ln n>0,
当m>0时,n>1,当m<0时,0当m<0时,易知y=emx是减函数,
当x→+∞时,y→0,f(x)→n2,故排除C,故选B.
5.已知函数f(x)为R上的奇函数,当x>0时,f(x)=-x;若a=0.3-0.25,b=log0.250.3,c=log0.32.5,则( )
A.f(b)C.f(c)答案:D
解析:当x>0时,f(x)=-x,由奇函数的性质知,
f(x)=-x,x∈R,函数单调递减;
又a=0.3-0.25>1,b=log0.250.3∈(0,1),c=log0.32.5<0
则a>b>c,
由函数单调递减知,f(a)故选D.
6.[2021·河北衡水中学三模]已知<1,则实数a的取值范围为( )
A. B.(0,1)
C.(1,+∞) D.
答案:A
解析:由loga<1,得a>1或0由a<1,得a>0,
由<1,得0∴当<1同时成立时,取交集得01.三招破解指数、对数、幂函数值的大小比较
(1)底数相同,指数不同的幂用指数函数的单调性进行比较;
(2)底数相同,真数不同的对数值用对数函数的单调性比较;
(3)底数不同、指数也不同,或底数不同、真数也不同的两个数,常引入中间量或结合图象比较大小.
2.[警示]
(1)对于含参数的指数、对数问题,在应用单调性时,要注意对底数进行讨论;
(2)解决对数问题时,首先要考虑定义域,其次再利用性质求解.
微专题2 函数零点与方程
『常考常用结论』
1.函数的零点及其与方程根的关系
对于函数f(x),使f(x)=0的实数x叫做函数f(x)的零点.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
2.零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
『提分题组训练』
1.函数f(x)=2sin x-sin 2x在[0,2π]的零点个数为( )
A.2 B.3
C.4 D.5
答案:B
解析:由f(x)=2sin x-sin 2x=2sin x-2sin x cos x=2sin x(1-cos x)=0,
得sin x=0或cos x=1,∵x∈[0,2π],
∴x=0、π或2π.
∴f(x)在[0,2π]的零点个数是3,故选B.
2.已知f(x)=若f(x)=1有两解,则a的取值范围是( )
A. B.
C.(1,2] D.(1,2)
答案:D
解析:由题意可知a>0且a≠1.
当1≤x<2时,由f(x)=logax=1,可得x=a;
当0由于方程f(x)=1有两解,则,解得1因此,实数a的取值范围是(1,2).故选D.
3.[2021·福建福州第一中学模拟]若曲线y=与x轴有且只有2个交点,则实数a的取值范围是( )
A.1≤a≤2 B.a≥3
C.1≤a≤2或a≥3 D.1≤a<2或a≥3
答案:D
解析:作出函数y=2x-4与y=(x-1)(x-3)的图象,
当a<1时,只有B一个零点;
当1≤a<2时,有A,B两个零点;
当2≤a<3时,有A一个零点;
当a≥3时,有A,C两个零点;
综上,实数a的取值范围是:1≤a<2或a≥3,故选D.
4.已知函数f(x)=,若关于x的方程f(x)=a有四个实数根,则实数a的取值范围为( )
A.(-∞,4) B.(0,3]
C.[3,4) D.(0,4)
答案:C
解析:作出函数f(x)的图象,
关于x的方程f(x)=a有四个实数根,则函数y=f(x)与y=a有四个交点,
则3≤a<4,故选C.
5.已知函数y=f(x)是定义在R上的偶函数,且f(2-x)=f(x),当0≤x≤1时,f(x)=x,设函数g(x)=f(x)-log5|x|,则g(x)的零点的个数为( )
A.6 B.7
C.8 D.9
答案:C
解析:由题意知:f(x)关于x=1对称,而g(x)的
零点即为f(x)=log5|x|的根,
又∵f(x)在R上的偶函数,知:f(x)∈[0,1]
且周期为2,关于y轴对称的函数,而-5≤x≤5
时log5|x|∈(-∞,1]且关于y轴对称,
∴f(x)与log5|x|在(0,+∞)的图象如下,
∴共有4个交点,由偶函数的对称性知:在(-∞,0)上也有4个交点,所以共8个交点.故选C.
6.已知函数f(x)=则函数y=f(f(x))的所有零点之和为________.
解析:x≤0时,x+1=0,x=-1,由f(x)=-1,可得x+1=-1或log2x=-1,∴x=-2或x=;
x>0时,log2x=0,x=1,由f(x)=1,可得x+1=1或log2x=1,∴x=0或x=2;
∴函数y=f(f(x))的所有零点为-2,,0,2,所以所有零点的和为-2++0+2=.
1.判断函数零点个数的方法
(1)直接法:解方程f(x)=0,方程有几个解,函数f(x)就有几个零点.
(2)图象法:画出函数f(x)的图象,函数f(x)的图象与x轴的交点个数即为函数f(x)的零点个数.
(3)将函数f(x)拆成两个常见函数h(x)和g(x)的差,从而f(x)=0 h(x)-g(x)=0 h(x)=g(x),则函数f(x)的零点个数即为函数y=h(x)与函数y=g(x)的图象的交点个数.
(4)二次函数的零点问题,通过相应的二次方程的判别式Δ来判断.
2.已知函数有零点(方程有根)求参数值(取值范围)常用的方法
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围.
(2)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
(3)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
微专题3 函数的实际应用
『保分题组训练』
1.[2021·全国甲卷(文)]青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为(≈1.259)( )
A.1.5 B.1.2
C.0.8 D.0.6
答案:C
解析:由题意知4.9=5+lg V,得lg V=-0.1,得V=≈0.8,所以该同学视力的小数记录法的数据约为0.8.
2.[2021·广东模拟]核酸检测分析是用荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时监测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量Xn与扩增次数n满足lg Xn=n lg (1+p)+lg X0,其中p为扩增效率,X0为DNA的初始数量.已知某被测标本DNA扩增10次后,数量变为原来的100倍,那么该样本的扩增效率p约为(参考数据:100.2≈1.585,10-0.2≈0.631)( )
A.0.369 B.0.415
C.0.585 D.0.631
答案:C
解析:由题意知,lg (100X0)=10lg (1+p)+lg X0,
即2+lg X0=10lg (1+p)+lg X0,
所以1+p=100.2≈1.585,解得p≈0.585.故选C.
3.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为v立方米,每天的进出水量为k立方米.已知污染源以每天r个单位污染河水,某一时段t(单位:天)河水污染质量指数为m(t)(每立方米河水所含的污染物)满足m(t)=(m0为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:ln 10≈2.30)( )
A.1个月 B.3个月
C.半年 D.1年
答案:C
解析:由题可知:m(t)==0.1m0
=0.1,
∴-t=ln 0.1≈-2.30,
∴t≈184(天)
∴要使河水的污染水平下降到初始时的10%,需要的时间大约是半年.
故选C.
4.[2021·湖南衡阳模拟]“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,那么在12 ℃时,该果蔬的保鲜时间为________小时.( )
A.72 B.36
C.24 D.16
答案:A
解析:当x=6时,e6a+b=216;当x=24时,e24a+b=8,
则==27,整理可得e6a=,于是eb=216×3=648,
当x=12时,y=e12a+b=(e6a)2·eb=×648=72.
故选A.
解决函数实际应用题的两个关键点
(1)认真读题,缜密审题,准确理解题意,明确问题的实际背景,然后进行科学地抽象概括,将实际问题归纳为相应的数学问题.
(2)要合理选取变量,设定变量之后,就要寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,建立相应的函数模型,最终求解数学模型使实际问题获解.
第2讲 基本初等函数、函数与方程——小题备考
微专题1 基本初等函数的图象与性质
微专题2 函数零点与方程
微专题3 函数的实际应用
微专题1
基本初等函数的图象与性质
『常考常用结论』
1.指数与对数式的七个运算公式
(1)am·an=am+n;
(2)(am)n=amn;
(3)loga(MN)=logaM+logaN;
(4)loga=logaM-logaN;
(5)logaMn=nlogaM;
(6)alogaN=N;
(7)logaN=.
注:a>0且a≠1,b>0且b≠1,M>0,N>0.
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分0
1.[2021·山东省实验中学二模]设a=50.3,b=log0.30.5,c=log30.4,则a,b,c的大小关系是( )
A.a
解析:由a=50.3>1>b=log0.30.5>0>c=log30.4,
∴c
答案:B
解析:当0
当a>1时,t=>0单调递减,f(t)=logat单调递增,所以f(x)=loga单调递减且定义域为(b,+∞),此时g(x)=bx+a与y轴的截距在(1,+∞)上.
∴当b>0时,g(x)单调递增;当b<0时,g(x)单调递减,故只有B符合要求.
故选B.
3.已知函数f(x)=ex-e-x-( )
A.是偶函数,且在(-∞,0)上单调递增
B.是奇函数,且在(-∞,0)上单调递减
C.是偶函数,且在(-∞,0)上单调递减
D.是奇函数,且在(-∞,0)上单调递增
答案:D
解析:因为f(x)=ex-e-x-,x∈(-∞,0)
所以f(-x)=e-x-ex+=-f(x),即函数为奇函数,
当x<0时,f(x)=ex-e-x-单调递增,
故选D.
4.[2021·湖南株洲二模]若函数f(x)=2的大致图象如图所示,则( )
A.m>0,0
C.m<0,0
答案:B
解析:令f(x)=0得emx=n,即mx=ln n,
解得x=ln n,
由图象知x=ln n>0,
当m>0时,n>1,当m<0时,0
当x→+∞时,y→0,f(x)→n2,故排除C,故选B.
5.已知函数f(x)为R上的奇函数,当x>0时,f(x)=-x;若a=0.3-0.25,b=log0.250.3,c=log0.32.5,则( )
A.f(b)
解析:当x>0时,f(x)=-x,由奇函数的性质知,
f(x)=-x,x∈R,函数单调递减;
又a=0.3-0.25>1,b=log0.250.3∈(0,1),c=log0.32.5<0
则a>b>c,
由函数单调递减知,f(a)
6.[2021·河北衡水中学三模]已知<1,则实数a的取值范围为( )
A. B.(0,1)
C.(1,+∞) D.
答案:A
解析:由loga<1,得a>1或0
由<1,得0
(1)底数相同,指数不同的幂用指数函数的单调性进行比较;
(2)底数相同,真数不同的对数值用对数函数的单调性比较;
(3)底数不同、指数也不同,或底数不同、真数也不同的两个数,常引入中间量或结合图象比较大小.
2.[警示]
(1)对于含参数的指数、对数问题,在应用单调性时,要注意对底数进行讨论;
(2)解决对数问题时,首先要考虑定义域,其次再利用性质求解.
微专题2 函数零点与方程
『常考常用结论』
1.函数的零点及其与方程根的关系
对于函数f(x),使f(x)=0的实数x叫做函数f(x)的零点.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
2.零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
『提分题组训练』
1.函数f(x)=2sin x-sin 2x在[0,2π]的零点个数为( )
A.2 B.3
C.4 D.5
答案:B
解析:由f(x)=2sin x-sin 2x=2sin x-2sin x cos x=2sin x(1-cos x)=0,
得sin x=0或cos x=1,∵x∈[0,2π],
∴x=0、π或2π.
∴f(x)在[0,2π]的零点个数是3,故选B.
2.已知f(x)=若f(x)=1有两解,则a的取值范围是( )
A. B.
C.(1,2] D.(1,2)
答案:D
解析:由题意可知a>0且a≠1.
当1≤x<2时,由f(x)=logax=1,可得x=a;
当0
3.[2021·福建福州第一中学模拟]若曲线y=与x轴有且只有2个交点,则实数a的取值范围是( )
A.1≤a≤2 B.a≥3
C.1≤a≤2或a≥3 D.1≤a<2或a≥3
答案:D
解析:作出函数y=2x-4与y=(x-1)(x-3)的图象,
当a<1时,只有B一个零点;
当1≤a<2时,有A,B两个零点;
当2≤a<3时,有A一个零点;
当a≥3时,有A,C两个零点;
综上,实数a的取值范围是:1≤a<2或a≥3,故选D.
4.已知函数f(x)=,若关于x的方程f(x)=a有四个实数根,则实数a的取值范围为( )
A.(-∞,4) B.(0,3]
C.[3,4) D.(0,4)
答案:C
解析:作出函数f(x)的图象,
关于x的方程f(x)=a有四个实数根,则函数y=f(x)与y=a有四个交点,
则3≤a<4,故选C.
5.已知函数y=f(x)是定义在R上的偶函数,且f(2-x)=f(x),当0≤x≤1时,f(x)=x,设函数g(x)=f(x)-log5|x|,则g(x)的零点的个数为( )
A.6 B.7
C.8 D.9
答案:C
解析:由题意知:f(x)关于x=1对称,而g(x)的
零点即为f(x)=log5|x|的根,
又∵f(x)在R上的偶函数,知:f(x)∈[0,1]
且周期为2,关于y轴对称的函数,而-5≤x≤5
时log5|x|∈(-∞,1]且关于y轴对称,
∴f(x)与log5|x|在(0,+∞)的图象如下,
∴共有4个交点,由偶函数的对称性知:在(-∞,0)上也有4个交点,所以共8个交点.故选C.
6.已知函数f(x)=则函数y=f(f(x))的所有零点之和为________.
解析:x≤0时,x+1=0,x=-1,由f(x)=-1,可得x+1=-1或log2x=-1,∴x=-2或x=;
x>0时,log2x=0,x=1,由f(x)=1,可得x+1=1或log2x=1,∴x=0或x=2;
∴函数y=f(f(x))的所有零点为-2,,0,2,所以所有零点的和为-2++0+2=.
1.判断函数零点个数的方法
(1)直接法:解方程f(x)=0,方程有几个解,函数f(x)就有几个零点.
(2)图象法:画出函数f(x)的图象,函数f(x)的图象与x轴的交点个数即为函数f(x)的零点个数.
(3)将函数f(x)拆成两个常见函数h(x)和g(x)的差,从而f(x)=0 h(x)-g(x)=0 h(x)=g(x),则函数f(x)的零点个数即为函数y=h(x)与函数y=g(x)的图象的交点个数.
(4)二次函数的零点问题,通过相应的二次方程的判别式Δ来判断.
2.已知函数有零点(方程有根)求参数值(取值范围)常用的方法
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围.
(2)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
(3)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
微专题3 函数的实际应用
『保分题组训练』
1.[2021·全国甲卷(文)]青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为(≈1.259)( )
A.1.5 B.1.2
C.0.8 D.0.6
答案:C
解析:由题意知4.9=5+lg V,得lg V=-0.1,得V=≈0.8,所以该同学视力的小数记录法的数据约为0.8.
2.[2021·广东模拟]核酸检测分析是用荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时监测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量Xn与扩增次数n满足lg Xn=n lg (1+p)+lg X0,其中p为扩增效率,X0为DNA的初始数量.已知某被测标本DNA扩增10次后,数量变为原来的100倍,那么该样本的扩增效率p约为(参考数据:100.2≈1.585,10-0.2≈0.631)( )
A.0.369 B.0.415
C.0.585 D.0.631
答案:C
解析:由题意知,lg (100X0)=10lg (1+p)+lg X0,
即2+lg X0=10lg (1+p)+lg X0,
所以1+p=100.2≈1.585,解得p≈0.585.故选C.
3.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为v立方米,每天的进出水量为k立方米.已知污染源以每天r个单位污染河水,某一时段t(单位:天)河水污染质量指数为m(t)(每立方米河水所含的污染物)满足m(t)=(m0为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:ln 10≈2.30)( )
A.1个月 B.3个月
C.半年 D.1年
答案:C
解析:由题可知:m(t)==0.1m0
=0.1,
∴-t=ln 0.1≈-2.30,
∴t≈184(天)
∴要使河水的污染水平下降到初始时的10%,需要的时间大约是半年.
故选C.
4.[2021·湖南衡阳模拟]“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,那么在12 ℃时,该果蔬的保鲜时间为________小时.( )
A.72 B.36
C.24 D.16
答案:A
解析:当x=6时,e6a+b=216;当x=24时,e24a+b=8,
则==27,整理可得e6a=,于是eb=216×3=648,
当x=12时,y=e12a+b=(e6a)2·eb=×648=72.
故选A.
解决函数实际应用题的两个关键点
(1)认真读题,缜密审题,准确理解题意,明确问题的实际背景,然后进行科学地抽象概括,将实际问题归纳为相应的数学问题.
(2)要合理选取变量,设定变量之后,就要寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,建立相应的函数模型,最终求解数学模型使实际问题获解.
同课章节目录
