北师大版九年级下册 2.2二次函数的图象与性质课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级下册 2.2二次函数的图象与性质课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 280.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 08:58:10 | ||
图片预览





文档简介
(共23张PPT)
第二章
2 二次函数的图象与性质
(第2课时)
知识回顾,问题引入
1.二次函数y=x2,y=-x2的图象是什么形状的?
2.二次函数y=x2,y=-x2的开口方向、对称轴、顶点坐标、增减性、最值是怎样的?
抛物线
可列表进行比较
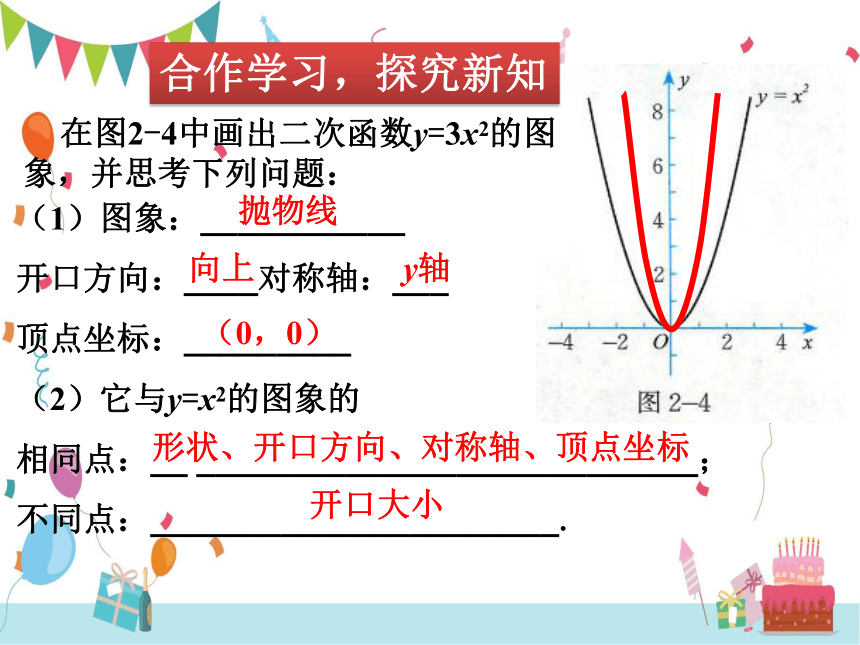
在图2-4中画出二次函数y=3x2的图象,并思考下列问题:
(1)图象:___________
开口方向:____对称轴:___
顶点坐标:_________
(2)它与y=x2的图象的
相同点:__ ___________________________;
不同点:______________________.
抛物线
向上
y轴
(0,0)
形状、开口方向、对称轴、顶点坐标
开口大小
合作学习,探究新知
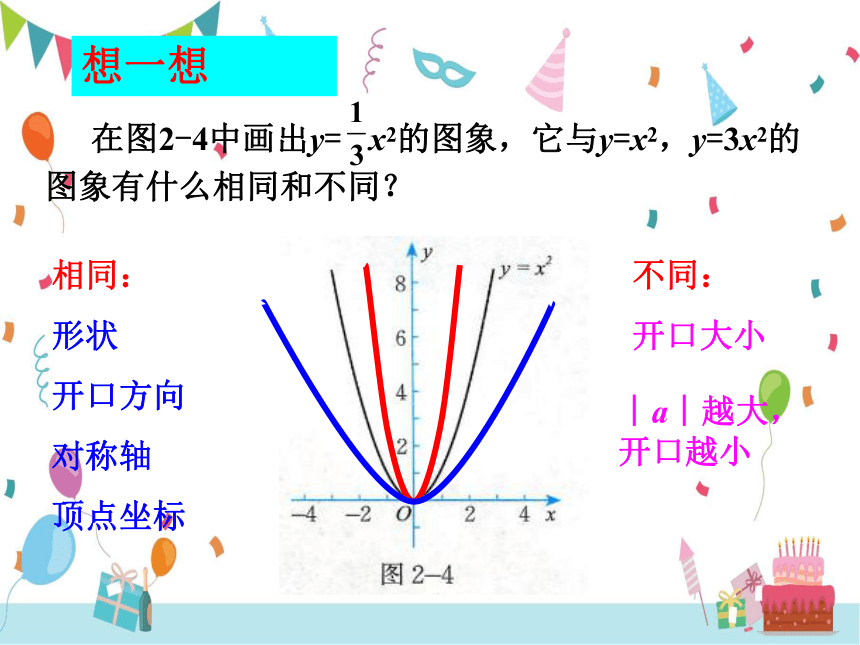
相同:
形状
开口方向
对称轴
顶点坐标
不同:
开口大小
︱a︱越大,开口越小
在图2-4中画出y= x2的图象,它与y=x2,y=3x2的图象有什么相同和不同?
想一想
函数y=ax2(a>0)的图象与性质
图象:
开口方向:______, 对称轴:______.
顶点坐标:_______.
向上
y轴
(0,0)
归纳
增减性:
x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
最值:
当x=0时,y取得最小值
y最小值=0
归纳
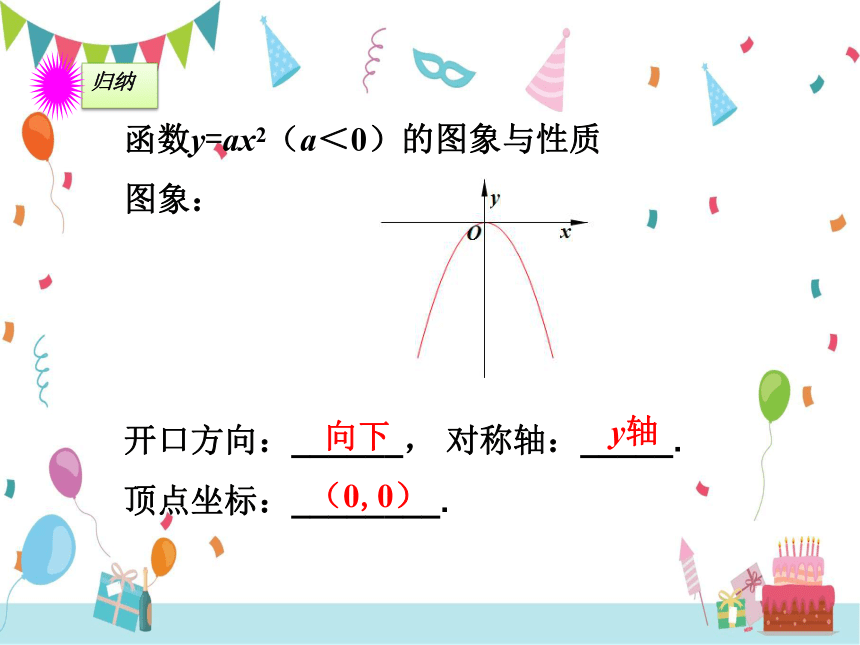
函数y=ax2(a<0)的图象与性质
图象:
开口方向:______, 对称轴:_____.
顶点坐标:________.
向下
y轴
(0,0)
归纳
增减性:
x<0时,y随x的增大而增大
x>0时,y随x的增大而减小
最值:
当x=0时,y取得最大值
y最大值=0
归纳
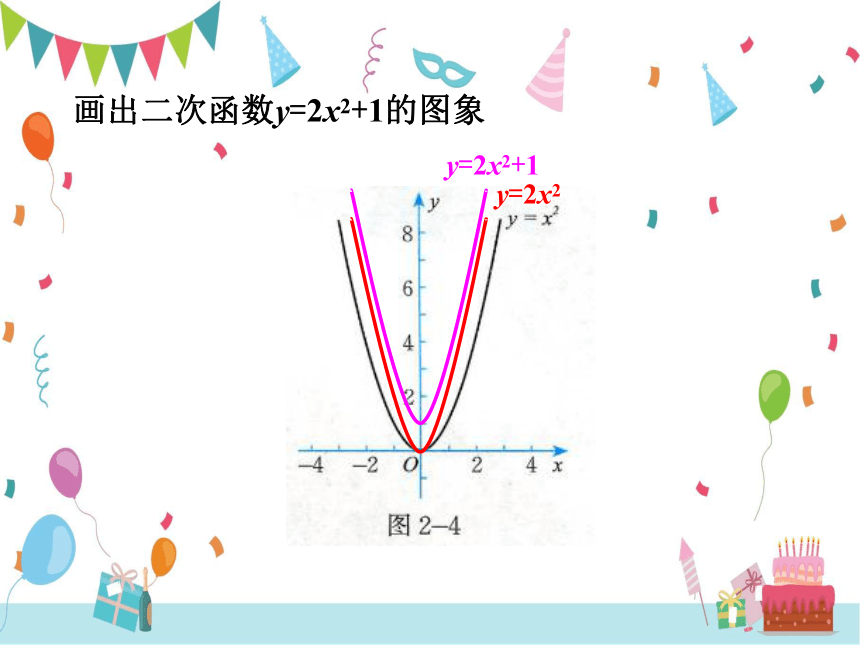
画出二次函数y=2x2+1的图象
y=2x2+1
y=2x2
y=2x2+1的图象:
由y=2x2的图象向上平移1个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,1)
二次函数y=2x2+1的图象的开口方向、对称轴、顶点坐标分别是什么?它与二次函数y=2x2的图象有什么关系?
y=2x2
y=2x2+1
y=2x2-1的图象:
由y=2x2的图象向下平移1个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,-1)
二次函数y=2x2-1的图象的开口方向、对称轴、顶点坐标分别是什么?它与二次函数y=2x2的图象有什么关系?
y=2x2
y=2x2-1
函数y=ax2+c(a>0)的图象与性质
平移:
由y=ax2向上或向下
平移︱c︱个单位得到
开口方向:
对称轴:
顶点坐标:
向上
y轴
(0,c)
归纳
增减性:
x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
最值:
当x=0时,y取得最小值
y最小值=c
归纳
函数y=ax2+c(a<0)的图象与性质
平移:
由y=ax2向上或向下
平移︱c︱个单位得到
开口方向:
对称轴:
顶点坐标:
向下
y轴
(0,c)
归纳
增减性:
x<0时,y随x的增大而增大
x>0时,y随x的增大而减小
最值:
当x=0时,y取得最大值
y最大值=c
归纳
抛物线y= x2+4是由抛物线y= x2怎样平移得到的?并说明:
(1)顶点坐标、对称轴及y随x的变化情况;
(2)函数的最值.
例题讲解
解 :抛物线y= x2+4是由抛物线 y= x2向上平移4个单位得到的.
(1)顶点坐标:(0,4)
对称轴:y轴
当x<0时,y随x的增大而减小,
当x<0时,y随x的增大而减小,
(2)函数的最值:y最小值=4
1.二次函数y=3x2- 的图象与二次函数
y=3x2的图象有什么关系?它是轴对
称图形吗?它的开口方向、对称轴、
顶点坐标分别是什么?画图看一看.
2.二次函数y=-2x2- 的图象与二次函
数y=-2x2+ 的图象有什么关系
随堂练习
y=3x2
y=3x2-
1.y=3x2- 的图象:
由y=3x2的图象向下平移
个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,- )
2. y=-2x2- 的图象:
由y=-2x2+ 的图象向下平移1个单位得到.
y=-2x2+
y=-2x2-
已知函数y=ax2+c的图象经过点
(1, )和(-3,-1).
(1)求函数的关系式;
(2)指出顶点坐标;
(3)求抛物线y=ax2+c与x轴的交点.
知识拓展
解:(1)由题意,得
解得
∴此函数的关系式为y=- x2+2.
(2)顶点坐标为(0,2).
(3)当y=0时,- x2+2=0.
解得 .
∴此抛物线与x轴交点为( ,0)(- ,0).
二次函数y=ax2的图象、
性质分别是什么
二次函数y=ax2+c的图象、
性质分别是什么
作业:习题2.3
抛物线y=ax2+c与y=ax2有怎样的关系
课堂小结
第二章
2 二次函数的图象与性质
(第2课时)
知识回顾,问题引入
1.二次函数y=x2,y=-x2的图象是什么形状的?
2.二次函数y=x2,y=-x2的开口方向、对称轴、顶点坐标、增减性、最值是怎样的?
抛物线
可列表进行比较
在图2-4中画出二次函数y=3x2的图象,并思考下列问题:
(1)图象:___________
开口方向:____对称轴:___
顶点坐标:_________
(2)它与y=x2的图象的
相同点:__ ___________________________;
不同点:______________________.
抛物线
向上
y轴
(0,0)
形状、开口方向、对称轴、顶点坐标
开口大小
合作学习,探究新知
相同:
形状
开口方向
对称轴
顶点坐标
不同:
开口大小
︱a︱越大,开口越小
在图2-4中画出y= x2的图象,它与y=x2,y=3x2的图象有什么相同和不同?
想一想
函数y=ax2(a>0)的图象与性质
图象:
开口方向:______, 对称轴:______.
顶点坐标:_______.
向上
y轴
(0,0)
归纳
增减性:
x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
最值:
当x=0时,y取得最小值
y最小值=0
归纳
函数y=ax2(a<0)的图象与性质
图象:
开口方向:______, 对称轴:_____.
顶点坐标:________.
向下
y轴
(0,0)
归纳
增减性:
x<0时,y随x的增大而增大
x>0时,y随x的增大而减小
最值:
当x=0时,y取得最大值
y最大值=0
归纳
画出二次函数y=2x2+1的图象
y=2x2+1
y=2x2
y=2x2+1的图象:
由y=2x2的图象向上平移1个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,1)
二次函数y=2x2+1的图象的开口方向、对称轴、顶点坐标分别是什么?它与二次函数y=2x2的图象有什么关系?
y=2x2
y=2x2+1
y=2x2-1的图象:
由y=2x2的图象向下平移1个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,-1)
二次函数y=2x2-1的图象的开口方向、对称轴、顶点坐标分别是什么?它与二次函数y=2x2的图象有什么关系?
y=2x2
y=2x2-1
函数y=ax2+c(a>0)的图象与性质
平移:
由y=ax2向上或向下
平移︱c︱个单位得到
开口方向:
对称轴:
顶点坐标:
向上
y轴
(0,c)
归纳
增减性:
x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
最值:
当x=0时,y取得最小值
y最小值=c
归纳
函数y=ax2+c(a<0)的图象与性质
平移:
由y=ax2向上或向下
平移︱c︱个单位得到
开口方向:
对称轴:
顶点坐标:
向下
y轴
(0,c)
归纳
增减性:
x<0时,y随x的增大而增大
x>0时,y随x的增大而减小
最值:
当x=0时,y取得最大值
y最大值=c
归纳
抛物线y= x2+4是由抛物线y= x2怎样平移得到的?并说明:
(1)顶点坐标、对称轴及y随x的变化情况;
(2)函数的最值.
例题讲解
解 :抛物线y= x2+4是由抛物线 y= x2向上平移4个单位得到的.
(1)顶点坐标:(0,4)
对称轴:y轴
当x<0时,y随x的增大而减小,
当x<0时,y随x的增大而减小,
(2)函数的最值:y最小值=4
1.二次函数y=3x2- 的图象与二次函数
y=3x2的图象有什么关系?它是轴对
称图形吗?它的开口方向、对称轴、
顶点坐标分别是什么?画图看一看.
2.二次函数y=-2x2- 的图象与二次函
数y=-2x2+ 的图象有什么关系
随堂练习
y=3x2
y=3x2-
1.y=3x2- 的图象:
由y=3x2的图象向下平移
个单位得到
开口方向:向上
对称轴:y轴
顶点坐标:(0,- )
2. y=-2x2- 的图象:
由y=-2x2+ 的图象向下平移1个单位得到.
y=-2x2+
y=-2x2-
已知函数y=ax2+c的图象经过点
(1, )和(-3,-1).
(1)求函数的关系式;
(2)指出顶点坐标;
(3)求抛物线y=ax2+c与x轴的交点.
知识拓展
解:(1)由题意,得
解得
∴此函数的关系式为y=- x2+2.
(2)顶点坐标为(0,2).
(3)当y=0时,- x2+2=0.
解得 .
∴此抛物线与x轴交点为( ,0)(- ,0).
二次函数y=ax2的图象、
性质分别是什么
二次函数y=ax2+c的图象、
性质分别是什么
作业:习题2.3
抛物线y=ax2+c与y=ax2有怎样的关系
课堂小结
