专题一 第2讲 基本初等函数、函数的应用 课件(共45张PPT)
文档属性
| 名称 | 专题一 第2讲 基本初等函数、函数的应用 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 03:52:47 | ||
图片预览



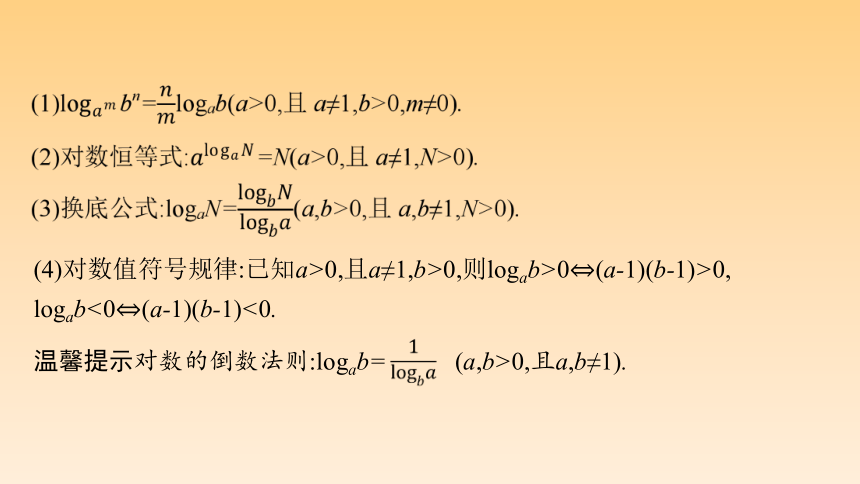








文档简介
(共45张PPT)
第2讲 基本初等函数、函数的应用
专题一
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
(4)对数值符号规律:已知a>0,且a≠1,b>0,则logab>0 (a-1)(b-1)>0,
logab<0 (a-1)(b-1)<0.
温馨提示对数的倒数法则:logab= (a,b>0,且a,b≠1).
2.指数函数与对数函数的图象和性质
(1)指数型函数y=k·amx+n+p(a>0,且a≠1)的图象经过的定点为 ,对数型函数y=k·
根据a0=1推知
loga(mx+n)+p(a>0,且a≠1)的图象所经过的定点为
根据loga1=0推知
(2)函数y=loga|x|(a>0,且a≠1)是偶函数,图象关于y轴对称,当a>1时,在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增;当0(3)函数y=|logax|(a>0,且a≠1)是非奇非偶函数,图象在x轴上方及x轴上,在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.
底数01时结论相同
3.函数的零点问题
(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.
温馨提示函数的零点是一个实数,而不是几何图形.
4.应用函数模型解决实际问题的一般步骤
关键能力 学案突破
突破点一
指数与对数运算
[例1-1] (多选题)(2021·广州一中月考)若10a=4,10b=25,则( )
A.a+b=2 B.b-a=1
答案 AC
解析 因为10a=4,10b=25,所以a=lg 4,b=lg 25,于是a+b=lg 4+lg 25=lg 100=2,故A正确;
[例1-2](2021·全国甲,理4)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为( ≈1.259)( )
A.1.5 B.1.2 C.0.8 D.0.6
答案 C
解析 由题意L=5+lg V,当L=4.9时,有4.9=5+lg V,lg V=-0.1,
规律总结指数、对数运算的常用方法与技巧
(1)将指数式与对数式进行互化,构造同底数的对数或指数式.
(2)逆用对数的运算性质,将同底数对数的和、差、倍化简.
(3)当对数的底数不同但真数相同时,可以取倒数,将其化为同底数的对数再进行运算.
(4)运用换底公式,转化对数的底数,再进行化简.
(2021·北京通州一模)著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为θ1 ℃,空气温度为θ0 ℃,则t min后物体的温度θ(单位:℃)满足:θ=θ0+(θ1-θ0)e-kt(其中k为常数,e=2.718 28…).现有某物体放在20 ℃的空气中冷却,2 min后测得物体的温度为52 ℃,再经过6 min物体的温度冷却到24 ℃,则该物体的初始温度是( )
A.80 ℃ B.82 ℃
C.84 ℃ D.86 ℃
对点练1
答案 C
突破点二
基本初等函数的图象与性质
[例2-1](2021·山东日照月考)当0答案 B
解析 由于0[例2-2](多选题)(2021·江苏盐城一模)已知函数f(x)=log2(1+4x)-x,则下列说法正确的是( )
A.函数f(x)是偶函数
B.函数f(x)是奇函数
C.函数f(x)在区间(-∞,0]上单调递增
D.函数f(x)的值域为[1,+∞)
答案 AD
则f(-x)=log2(2-x+2x)=f(x),所以f(x)是偶函数,因此A选项正确,B选项错误;
令g(x)=2x+2-x,则g'(x)=2xln 2-2-xln 2=ln 2(2x-2-x),当x≤0时,g'(x)≤0且不恒为零,所以g(x)在区间(-∞,0]上单调递减,于是f(x)=log2g(x)在区间(-∞,0]上单调递减.故C选项错误;
技巧点拨基本初等函数的图象与性质应用技巧
(1)指数函数与对数函数的图象分别经过定点(0,1)和(1,0),在进行图象识别与判断中注意对图象所经过定点的分析.
(2)与指数函数和对数函数有关的函数的奇偶性,在利用定义判断时,注意对f(-x)表达式的变形与转化,以便得出f(x)与f(-x)的关系.
(3)由指数函数、对数函数与其他函数复合而成的函数,其性质的研究往往通过换元法转化为两个基本初等函数的有关性质,然后根据复合函数的性质与相关函数的性质之间的关系进行判断.
对点练2
A.aC.b(2)(多选题)(2021·辽宁抚顺模拟)已知函数f(x)= 则下列结论正确的是( )
A.函数f(x)的定义域为R
B.函数f(x)在R上为增函数
C.函数f(x)的值域为(-3,+∞)
D.函数f(x)只有一个零点
答案 (1)B (2)AC
(2)对于选项A:由已知可得函数定义域为R,故A正确;
对于选项B:当x<1时,函数f(x)单调递增,当x≥1时,函数f(x)单调递增,但
41-3=1>ln 1=0,所以函数在R上不单调,故B错误;
对于选项C:当x<1时,-3(-3,+∞),故C正确;
对于选项D:当x<1时,令4x-3=0,解得x=log43,当x≥1时,令ln x=0,解得x=1,故函数f(x)有两个零点,所以D错误,故选AC.
突破点三
函数的零点及其应用
命题角度1 确定函数零点的个数或范围
[例3-1](2021·山东聊城月考)函数f(x)=ex+x-2的零点所在区间为( )
A.(-1,0)
B.(0,1)
C.(1,2)
D.(2,3)
答案 B
A.1 B.2
C.3 D.4
答案 C
解析 令f(x)=t,当f(t)=0时,解得t= 或t=-1.
在同一平面直角坐标系中分别画出函数y=f(x),y=-1,y= 的图象(如图所示),由图可知,y=f(x)的图象与直线y=-1有1个交点,y=f(x)的图象与直线y=有2个交点,故y=f(f(x))的零点个数为3.故选C.
方法点拨函数零点个数的判断方法
(1)直接法求零点:令f(x)=0,如果能求出解,则方程有几个解,函数f(x)就有几个零点.
(2)零点存在性定理:若函数f(x)在区间[a,b]上的图象是连续不断的曲线,且f(a)·f(b)<0,则结合函数的性质(如单调性、奇偶性)即可确定函数f(x)零点的个数.
(3)利用图象交点的个数:将函数变形为两个函数的差,画出两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
(4)形如f(g(x))的函数,可采用换元法,先令g(x)=t,求得当f(t)=0时t的值,然后根据函数g(x)的图象及性质确定当g(x)=t时x的值的个数即为f(g(x))的零点的个数,解答时注意数形结合,注意对函数f(x)与g(x)图象及性质的分析.
对点练3
(1)(2021·辽宁锦州期末)已知函数f(x)=x2-4x-1+ex-2+e-x+2有两个零点x1,x2,则x1+x2=( )
A.2 B.4
C.5 D.6
(2)(2021·吉林长春二模)若函数f(x)= 则函数g(x)=f(f(x))-2的零点个数为( )
A.3 B.4
C.5 D.6
答案(1)B (2) B
解析 (1)函数f(x)=x2-4x-1+ex-2+e-x+2=(x-2)2+ex-2+e-x+2-5,令t=x-2,则f(x)=g(t)=t2+et+e-t-5,g(-t)=t2+et+e-t-5=g(t),所以g(t)是偶函数,所以函数f(x)的图象关于直线x=2对称,又函数f(x)=x2-4x-1+ex-2+e-x+2有两个零点x1,x2,则x1+x2=4,故选B.
(2)原题等价于求方程f(f(x))=2的根的个数.
令t=f(x),则f(f(x))=2等价于f(t)=2,如图1,可知方程f(t)=2有两个不相等的实数根,且t1=log23,t2= ,如图2,可知方程t1=log23=f(x),t2= =f(x)各有两个不相等的实数根,故原函数共有4个零点.故选B.
图1
图2
命题角度2 根据函数零点求参数的取值范围
答案 D
解析 由函数y=f(x)-a有两个零点,可得y=f(x)的图象与直线y=a有两个不同的交点.
方法点睛已知函数有零点(方程有根)求参数值(取值范围)常用的方法
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数的取值范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题进行求解.
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出两个函数的图象,利用数形结合的方法求解.
对点练4
答案 D
解析 由题意可知x=0为g(x)的一个零点.
函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,即函数f(x)与h(x)=|kx2-2x|(k∈R)的图象有4个交点,其中(0,0)为一个交点,当x>0时,由x3=|kx2-2x|可得x2=|kx-2|,当x<0时,由-x=|kx2-2x|可得1=|kx-2|.令φ(x)= (x)=|kx-2|,即函数φ(x)与μ(x)的图象有3个交点.
图1
图2
突破点四
函数模型及其应用
[例4](2021·北京西城区一模)长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益.每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数=(水库实际蓄水量)÷(水库总蓄水量)×100)来衡量每座水库的水位情况.假设某次联合调度要求如下:
a.调度后每座水库的蓄满指数仍属于区间[0,100];
b.调度后每座水库的蓄满指数都不能降低;
c.调度前后,各水库之间的蓄满指数排名不变.
答案 ②④
方法总结函数模型应用问题的两个关键点
(1)认真读题,缜密审题,正确理解题意,明确问题的实际背景,然后进行抽象概括,将实际问题转化为数学问题.
(2)合理建立函数模型,选取恰当的变量,寻找变量之间的内在联系,用恰当的代数式表示变量之间的关系,然后利用函数知识解决数学问题,从而解决实际问题.
对点练5
(2021·辽宁大连一模)某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元及500元以内的部分按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.413.7元 B.513.7元
C.546.6元 D.548.7元
答案 C
解析 某人两次去购物,分别付款168元与423元,根据商场的优惠规定,168元的商品未优惠,而423元的商品是按九折优惠后的,则实际商品价格为423÷0.9=470(元),如果他一次性购买同样的商品即价值168+470=638(元)的商品时,应付款500×0.9+(638-500)×0.7=450+96.6=546.6(元).故选C.
第2讲 基本初等函数、函数的应用
专题一
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
(4)对数值符号规律:已知a>0,且a≠1,b>0,则logab>0 (a-1)(b-1)>0,
logab<0 (a-1)(b-1)<0.
温馨提示对数的倒数法则:logab= (a,b>0,且a,b≠1).
2.指数函数与对数函数的图象和性质
(1)指数型函数y=k·amx+n+p(a>0,且a≠1)的图象经过的定点为 ,对数型函数y=k·
根据a0=1推知
loga(mx+n)+p(a>0,且a≠1)的图象所经过的定点为
根据loga1=0推知
(2)函数y=loga|x|(a>0,且a≠1)是偶函数,图象关于y轴对称,当a>1时,在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增;当0
底数0
3.函数的零点问题
(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.
温馨提示函数的零点是一个实数,而不是几何图形.
4.应用函数模型解决实际问题的一般步骤
关键能力 学案突破
突破点一
指数与对数运算
[例1-1] (多选题)(2021·广州一中月考)若10a=4,10b=25,则( )
A.a+b=2 B.b-a=1
答案 AC
解析 因为10a=4,10b=25,所以a=lg 4,b=lg 25,于是a+b=lg 4+lg 25=lg 100=2,故A正确;
[例1-2](2021·全国甲,理4)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为( ≈1.259)( )
A.1.5 B.1.2 C.0.8 D.0.6
答案 C
解析 由题意L=5+lg V,当L=4.9时,有4.9=5+lg V,lg V=-0.1,
规律总结指数、对数运算的常用方法与技巧
(1)将指数式与对数式进行互化,构造同底数的对数或指数式.
(2)逆用对数的运算性质,将同底数对数的和、差、倍化简.
(3)当对数的底数不同但真数相同时,可以取倒数,将其化为同底数的对数再进行运算.
(4)运用换底公式,转化对数的底数,再进行化简.
(2021·北京通州一模)著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为θ1 ℃,空气温度为θ0 ℃,则t min后物体的温度θ(单位:℃)满足:θ=θ0+(θ1-θ0)e-kt(其中k为常数,e=2.718 28…).现有某物体放在20 ℃的空气中冷却,2 min后测得物体的温度为52 ℃,再经过6 min物体的温度冷却到24 ℃,则该物体的初始温度是( )
A.80 ℃ B.82 ℃
C.84 ℃ D.86 ℃
对点练1
答案 C
突破点二
基本初等函数的图象与性质
[例2-1](2021·山东日照月考)当0
解析 由于0
A.函数f(x)是偶函数
B.函数f(x)是奇函数
C.函数f(x)在区间(-∞,0]上单调递增
D.函数f(x)的值域为[1,+∞)
答案 AD
则f(-x)=log2(2-x+2x)=f(x),所以f(x)是偶函数,因此A选项正确,B选项错误;
令g(x)=2x+2-x,则g'(x)=2xln 2-2-xln 2=ln 2(2x-2-x),当x≤0时,g'(x)≤0且不恒为零,所以g(x)在区间(-∞,0]上单调递减,于是f(x)=log2g(x)在区间(-∞,0]上单调递减.故C选项错误;
技巧点拨基本初等函数的图象与性质应用技巧
(1)指数函数与对数函数的图象分别经过定点(0,1)和(1,0),在进行图象识别与判断中注意对图象所经过定点的分析.
(2)与指数函数和对数函数有关的函数的奇偶性,在利用定义判断时,注意对f(-x)表达式的变形与转化,以便得出f(x)与f(-x)的关系.
(3)由指数函数、对数函数与其他函数复合而成的函数,其性质的研究往往通过换元法转化为两个基本初等函数的有关性质,然后根据复合函数的性质与相关函数的性质之间的关系进行判断.
对点练2
A.a
A.函数f(x)的定义域为R
B.函数f(x)在R上为增函数
C.函数f(x)的值域为(-3,+∞)
D.函数f(x)只有一个零点
答案 (1)B (2)AC
(2)对于选项A:由已知可得函数定义域为R,故A正确;
对于选项B:当x<1时,函数f(x)单调递增,当x≥1时,函数f(x)单调递增,但
41-3=1>ln 1=0,所以函数在R上不单调,故B错误;
对于选项C:当x<1时,-3
对于选项D:当x<1时,令4x-3=0,解得x=log43,当x≥1时,令ln x=0,解得x=1,故函数f(x)有两个零点,所以D错误,故选AC.
突破点三
函数的零点及其应用
命题角度1 确定函数零点的个数或范围
[例3-1](2021·山东聊城月考)函数f(x)=ex+x-2的零点所在区间为( )
A.(-1,0)
B.(0,1)
C.(1,2)
D.(2,3)
答案 B
A.1 B.2
C.3 D.4
答案 C
解析 令f(x)=t,当f(t)=0时,解得t= 或t=-1.
在同一平面直角坐标系中分别画出函数y=f(x),y=-1,y= 的图象(如图所示),由图可知,y=f(x)的图象与直线y=-1有1个交点,y=f(x)的图象与直线y=有2个交点,故y=f(f(x))的零点个数为3.故选C.
方法点拨函数零点个数的判断方法
(1)直接法求零点:令f(x)=0,如果能求出解,则方程有几个解,函数f(x)就有几个零点.
(2)零点存在性定理:若函数f(x)在区间[a,b]上的图象是连续不断的曲线,且f(a)·f(b)<0,则结合函数的性质(如单调性、奇偶性)即可确定函数f(x)零点的个数.
(3)利用图象交点的个数:将函数变形为两个函数的差,画出两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
(4)形如f(g(x))的函数,可采用换元法,先令g(x)=t,求得当f(t)=0时t的值,然后根据函数g(x)的图象及性质确定当g(x)=t时x的值的个数即为f(g(x))的零点的个数,解答时注意数形结合,注意对函数f(x)与g(x)图象及性质的分析.
对点练3
(1)(2021·辽宁锦州期末)已知函数f(x)=x2-4x-1+ex-2+e-x+2有两个零点x1,x2,则x1+x2=( )
A.2 B.4
C.5 D.6
(2)(2021·吉林长春二模)若函数f(x)= 则函数g(x)=f(f(x))-2的零点个数为( )
A.3 B.4
C.5 D.6
答案(1)B (2) B
解析 (1)函数f(x)=x2-4x-1+ex-2+e-x+2=(x-2)2+ex-2+e-x+2-5,令t=x-2,则f(x)=g(t)=t2+et+e-t-5,g(-t)=t2+et+e-t-5=g(t),所以g(t)是偶函数,所以函数f(x)的图象关于直线x=2对称,又函数f(x)=x2-4x-1+ex-2+e-x+2有两个零点x1,x2,则x1+x2=4,故选B.
(2)原题等价于求方程f(f(x))=2的根的个数.
令t=f(x),则f(f(x))=2等价于f(t)=2,如图1,可知方程f(t)=2有两个不相等的实数根,且t1=log23,t2= ,如图2,可知方程t1=log23=f(x),t2= =f(x)各有两个不相等的实数根,故原函数共有4个零点.故选B.
图1
图2
命题角度2 根据函数零点求参数的取值范围
答案 D
解析 由函数y=f(x)-a有两个零点,可得y=f(x)的图象与直线y=a有两个不同的交点.
方法点睛已知函数有零点(方程有根)求参数值(取值范围)常用的方法
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数的取值范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题进行求解.
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出两个函数的图象,利用数形结合的方法求解.
对点练4
答案 D
解析 由题意可知x=0为g(x)的一个零点.
函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,即函数f(x)与h(x)=|kx2-2x|(k∈R)的图象有4个交点,其中(0,0)为一个交点,当x>0时,由x3=|kx2-2x|可得x2=|kx-2|,当x<0时,由-x=|kx2-2x|可得1=|kx-2|.令φ(x)= (x)=|kx-2|,即函数φ(x)与μ(x)的图象有3个交点.
图1
图2
突破点四
函数模型及其应用
[例4](2021·北京西城区一模)长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益.每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数=(水库实际蓄水量)÷(水库总蓄水量)×100)来衡量每座水库的水位情况.假设某次联合调度要求如下:
a.调度后每座水库的蓄满指数仍属于区间[0,100];
b.调度后每座水库的蓄满指数都不能降低;
c.调度前后,各水库之间的蓄满指数排名不变.
答案 ②④
方法总结函数模型应用问题的两个关键点
(1)认真读题,缜密审题,正确理解题意,明确问题的实际背景,然后进行抽象概括,将实际问题转化为数学问题.
(2)合理建立函数模型,选取恰当的变量,寻找变量之间的内在联系,用恰当的代数式表示变量之间的关系,然后利用函数知识解决数学问题,从而解决实际问题.
对点练5
(2021·辽宁大连一模)某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元及500元以内的部分按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.413.7元 B.513.7元
C.546.6元 D.548.7元
答案 C
解析 某人两次去购物,分别付款168元与423元,根据商场的优惠规定,168元的商品未优惠,而423元的商品是按九折优惠后的,则实际商品价格为423÷0.9=470(元),如果他一次性购买同样的商品即价值168+470=638(元)的商品时,应付款500×0.9+(638-500)×0.7=450+96.6=546.6(元).故选C.
同课章节目录
