北师大新版九年级(下)《第3章+圆》常考题套卷(3)(word版、含解析)
文档属性
| 名称 | 北师大新版九年级(下)《第3章+圆》常考题套卷(3)(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 745.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 21:37:23 | ||
图片预览

文档简介
北师大新版九年级(下)《第3章 圆》常考题套卷(3)
一、选择题(共10小题)
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
2.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π B.4π C.12π D.24π
3.如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A. B. C. D.
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
5.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
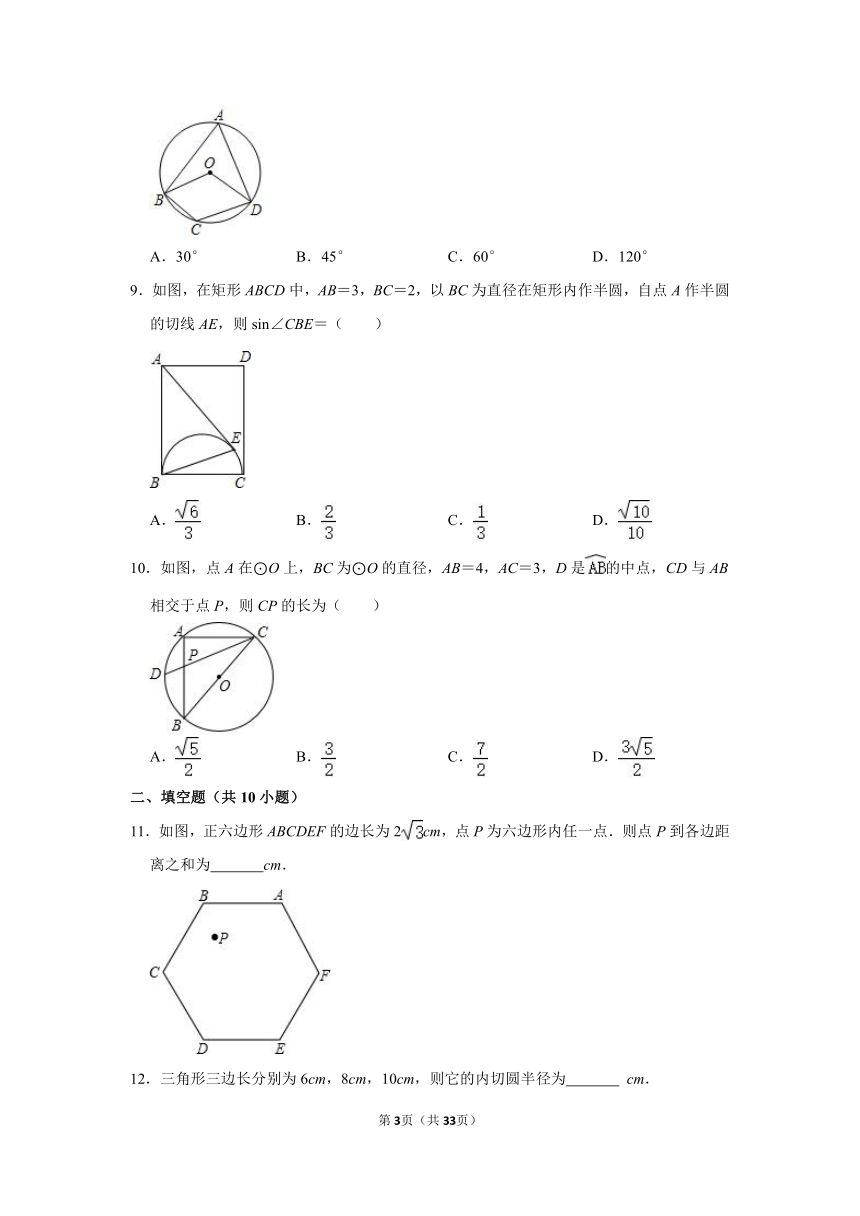
6.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,
①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;
②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;
下面有四个结论:
①CD+EF=AB
②
③∠CO2D+∠EO3F=∠AO1B
④∠CDO2+∠EFO3=∠P
所有正确结论的序号是( )
A.①②③④ B.①②③ C.②④ D.②③④
7.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为( )
A.90° B.115° C.125° D.180°
8.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
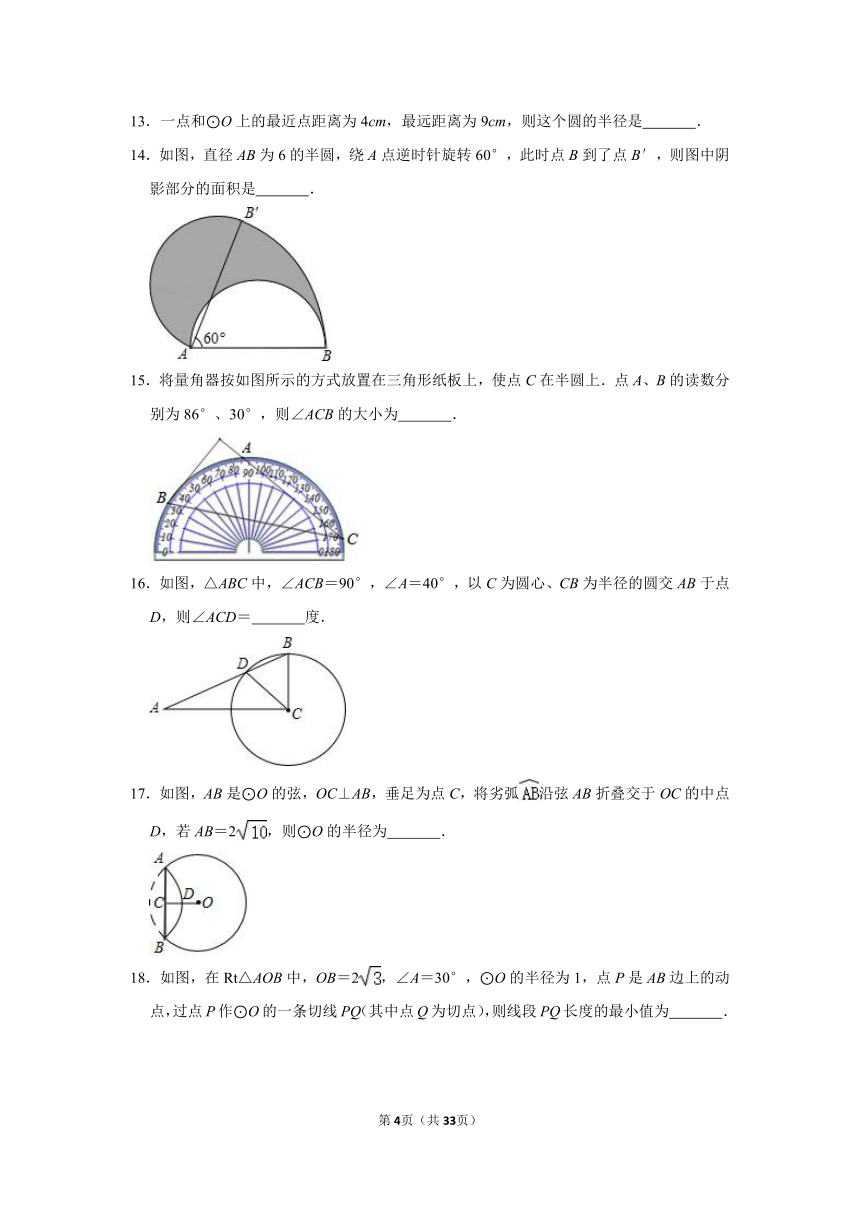
9.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
10.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
二、填空题(共10小题)
11.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为 cm.
12.三角形三边长分别为6cm,8cm,10cm,则它的内切圆半径为 cm.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 .
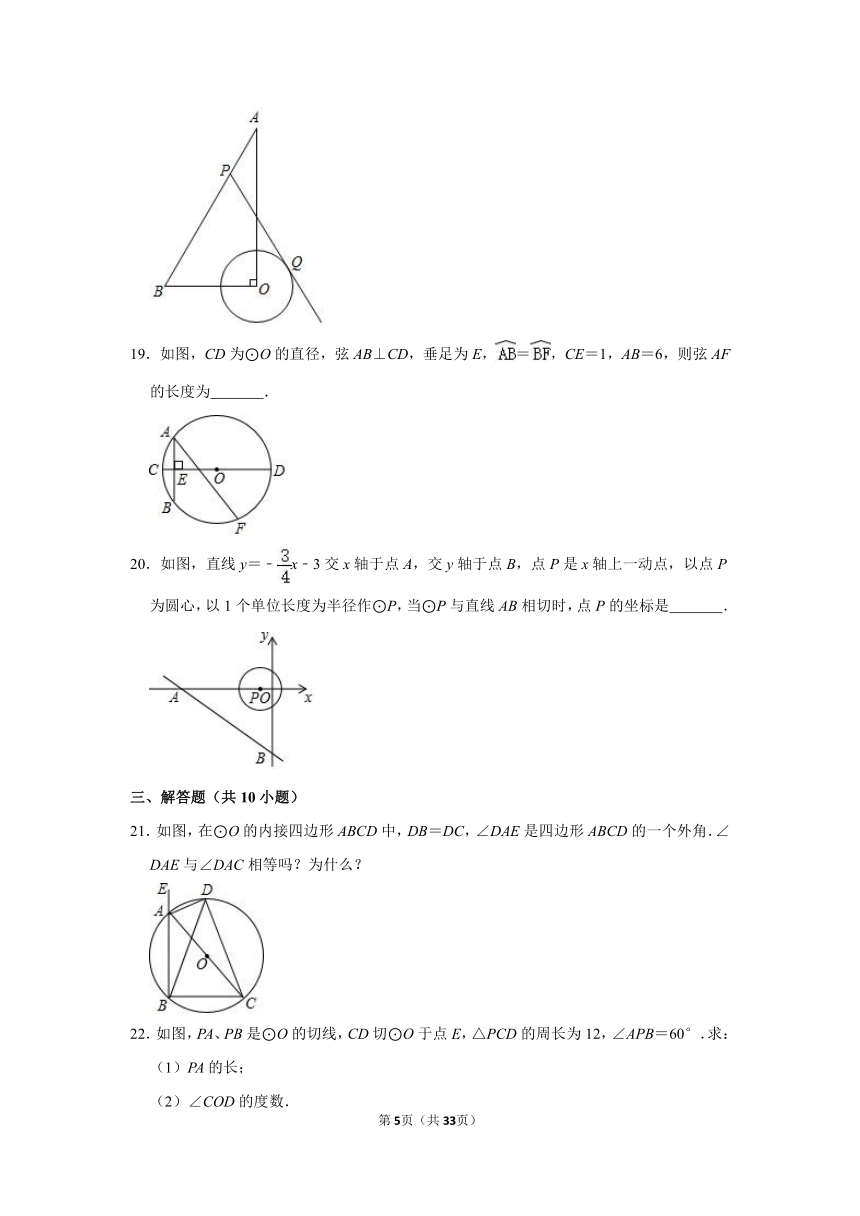
14.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
15.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
16.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD= 度.
17.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
18.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
19.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
20.如图,直线y=﹣x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 .
三、解答题(共10小题)
21.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
23.如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
24.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
25.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
26.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
27.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE
(1)求证:OA=OB;
(2)已知AB=4 ,OA=4,求阴影部分的面积.
28.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
29.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
30.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
求证:(1)AC是⊙D的切线;
(2)AB+EB=AC.
北师大新版九年级(下)《第3章 圆》常考题套卷(3)
参考答案与试题解析
一、选择题(共10小题)
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
【解答】解:连接OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
2.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π B.4π C.12π D.24π
【解答】解:S==12π,
故选:C.
3.如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A. B. C. D.
【解答】解:作AH⊥BC于H,如图,BE=2t,BD=8﹣2t,
∵AB=AC=5,
∴BH=CH=BC=4,
当BE⊥DE,直线DE与⊙O相切,则∠BED=90°,
∵∠EBD=∠ABH,
∴△BED∽△BHA,
∴=,即=,解得t=.
故选:A.
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
5.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
【解答】解:∵点M的坐标是(4,3),
∴点M到x轴的距离是3,到y轴的距离是4,
∵点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,
∴r的取值范围是3<r<4,
故选:D.
6.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,
①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;
②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;
下面有四个结论:
①CD+EF=AB
②
③∠CO2D+∠EO3F=∠AO1B
④∠CDO2+∠EFO3=∠P
所有正确结论的序号是( )
A.①②③④ B.①②③ C.②④ D.②③④
【解答】解:由题意得,AP=CD,BP=EF,
∵AP+BP>AB,
∴CD+EF>AB;
∵⊙O1,⊙O2,⊙O3是等圆,
∴=,=,
∵+=,
∴+=;
∴∠CO2D=∠AO1P,∠EO3F=∠BO1P,
∵∠AO1P+∠BO1P=∠AO1P,
∴∠CO2D+∠EO3F=∠AO1B;
∵∠CDO2=∠APO1,∠BPO1=∠EFO3,
∵∠P=∠APO1+∠BPO1,
∴∠CDO2+∠EFO3=∠P,
∴正确结论的序号是②③④,
故选:D.
7.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为( )
A.90° B.115° C.125° D.180°
【解答】解:本题中弧长应该是10cm,
根据半径为5cm,那么5×π×n÷180=10,
那么圆心角n≈115°.
故选:B.
8.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
【解答】解:设∠BAD=x,则∠BOD=2x,
∵∠BCD=∠BOD=2x,∠BAD+∠BCD=180°,
∴3x=180°,
∴x=60°,
∴∠BAD=60°,
故选:C.
9.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
【解答】解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F,
∵AB,AE都为圆的切线,
∴AE=AB,
∵OB=OE,AO=AO,
∴△ABO≌△AEO(SSS),
∴∠OAB=∠OAE,
∴AO⊥BE,
在直角△AOB里AO2=OB2+AB2,
∵OB=1,AB=3,
∴AO=,
易证明△BOF∽△AOB,
∴BO:AO=OF:OB,
∴1:=OF:1,
∴OF=,
sin∠CBE==,
故选:D.
10.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
【解答】解:如图作PH⊥BC于H.
∵=,
∴∠ACD=∠BCD,
∵BC是直径,
∴∠BAC=90°,
∴PA⊥AC,∵PH⊥BC,
∴PA=PH,设PA=PH=x,
∵PC=PC,
∴Rt△PCA≌Rt△PCH,
∴AC=CH=3,
∵BC==5,
∴BH=2,
在Rt△PBH中,∵PB2=PH2+BH2,
∴(4﹣x)2=x2+22,
解得x=,
∴PC==,
故选:D.
二、填空题(共10小题)
11.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为 18 cm.
【解答】解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2×=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
12.三角形三边长分别为6cm,8cm,10cm,则它的内切圆半径为 2 cm.
【解答】解:如图所示:△ABC中,AC=6,BC=8,AB=10,
∵62+82=102,即AC2+BC2=AB2,
∴△ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵CD=CE,BE=BF,AF=AD,
∵OD⊥AC,OE⊥BC,
∴四边形ODCE是正方形,即CD=CE=R,
∴AC﹣CD=AB﹣BF,即6﹣R=10﹣BF①
BC﹣CE=AB﹣AF,即8﹣R=BF②,
①②联立得,R=2.
故答案为:2.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 6.5cm或2.5cm .
【解答】解:点P应分为位于圆的内部与外部两种情况讨论:
①当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是4+9=13cm,因而半径是6.5cm;
②当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是9﹣4=5cm,因而半径是2.5cm.
故答案为6.5cm或2.5cm.
14.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 6π .
【解答】解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
15.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 28° .
【解答】解:设半圆圆心为O,连OA,OB,如图,
∵∠ACB=∠AOB,
而∠AOB=86°﹣30°=56°,
∴∠ACB=×56°=28°.
故答案为:28°.
16.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD= 10 度.
【解答】解:∵△ABC中,∠ACB=90°,∠A=40°
∴∠B=50°
∵BC=CD
∴∠B=∠BDC=50°
∴∠BCD=80°
∴∠ACD=10°.
17.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 3 .
【解答】解:连接OA,设半径为x,
∵将劣弧沿弦AB折叠交于OC的中点D,
∴OC=,OC⊥AB,
∴AC==,
∵OA2﹣OC2=AC2,
∴,
解得,x=3.
故答案为:3.
18.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 2 .
【解答】解:连接OP、OQ,作OP′⊥AB于P′,
∵PQ是⊙O的切线,
∴OQ⊥PQ,
∴PQ==,
当OP最小时,线段PQ的长度最小,
当OP⊥AB时,OP最小,
在Rt△AOB中,∠A=30°,
∴OA==6,
在Rt△AOP′中,∠A=30°,
∴OP′=OA=3,
∴线段PQ长度的最小值==2,
故答案为:2.
19.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
【解答】解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
20.如图,直线y=﹣x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 (﹣,0)或P(﹣,0) .
【解答】解:∵直线y=﹣x﹣3交x轴于点A,交y轴于点B,
∴令x=0,得y=﹣3,令y=0,得x=﹣4,
∴A(﹣4,0),B(0,﹣3),
∴OA=4,OB=3,
∴AB=5,
设⊙P与直线AB相切于D,
连接PD,
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴=,
∴=,
∴AP=,
∴OP=或OP=,
∴P(﹣,0)或P(﹣,0),
故答案为:(﹣,0)或P(﹣,0).
三、解答题(共10小题)
21.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
【解答】解:∠DAE与∠DAC相等,
理由:∵DB=DC,
∠DBC=∠DCB,
∵∠DAE是四边形ABCD的一个外角,
∴∠EAD=∠DCB,
∴∠DBC=∠EAD,
又∵∠DAC=∠DBC,
∴∠DAE=∠DAC.
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
【解答】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
23.如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
【解答】(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,
∴AD为⊙O的直径,
∴∠AED=90°,
∴∠ACB=∠AED.
∵AD是△ABC中∠BAC的平分线,
∴∠CAD=∠EAD,
∴CD=DE,
在Rt△ACD与Rt△AED中,
,
∴△ACD≌△AED(HL),
∴AC=AE;
(2)∵△ABC是直角三角形,且AC=6,BC=8,
∴AB===10,
∵由(1)得,∠AED=90°,
∴∠BED=90°.
设CD=DE=x,则DB=BC﹣CD=8﹣x,EB=AB﹣AE=10﹣6=4,
在Rt△BED中,根据勾股定理得,BD2=BE2+ED2,即(8﹣x)2=x2+42,解得x=3,
∴CD=3,
∵AC=6,△ACD是直角三角形,
∴AD2=AC2+CD2=62+32=45,
∴AD=3.
解法二:由△BDE∽△BAC,
可得=,可得DE=3,
∴AD===3.
24.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O是AB的中点,
∴S△POB=S△PAB=×AP PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
25.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
【解答】解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
26.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 60° ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
【解答】解:(1)如图1,连接OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°,
∠E的度数为60°;
(2)①如图2,直线AD,CB交于点E,连接OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连接OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
27.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE
(1)求证:OA=OB;
(2)已知AB=4 ,OA=4,求阴影部分的面积.
【解答】解:(1)连接OC,
∵AB与⊙O相切于点C
∴∠ACO=90°,
∵CD=CE
∴=,
∴∠AOC=∠BOC,
∴∠A=∠B
∴OA=OB,
(2)由(1)可知:△OAB是等腰三角形,
∴BC=AB=2,
∴sin∠COB==,
∴∠COB=60°,
∴∠B=30°,
∴OC=OB=2,
∴扇形OCE的面积为:=,
△OCB的面积为:×2×2=2,
S阴影=2﹣π.
28.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
【解答】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:π×132=169π(cm2).
29.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
【解答】解:(1)相切,理由如下:
连接AD,OD,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD∥AC.
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠ODE=∠CED=90°.
∴OD⊥DE.
∴DE与⊙O相切.
(2)由(1)知∠ADC=90°,
∴在Rt△ADC中,由勾股定理 得
AD==4.
∵SACD=AD CD=AC DE,
∴×4×3=×5DE.
∴DE=.
30.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
求证:(1)AC是⊙D的切线;
(2)AB+EB=AC.
【解答】解:(1)过点D作DF⊥AC于F;
∵AB为⊙D的切线,
∴∠B=90°
∴AB⊥BC
∵AD平分∠BAC,DF⊥AC
∴BD=DF
∴AC与⊙D相切;
(2)在△BDE和△DCF中,
∵BD=DF,DE=DC,
在Rt△BDE和Rt△DCF中,
,
∴Rt△BDE≌Rt△DCF(HL),
∴EB=FC.
∵AB=AF,
∴AB+EB=AF+FC,
即AB+EB=AC.
第1页(共3页)
一、选择题(共10小题)
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
2.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π B.4π C.12π D.24π
3.如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A. B. C. D.
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
5.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
6.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,
①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;
②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;
下面有四个结论:
①CD+EF=AB
②
③∠CO2D+∠EO3F=∠AO1B
④∠CDO2+∠EFO3=∠P
所有正确结论的序号是( )
A.①②③④ B.①②③ C.②④ D.②③④
7.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为( )
A.90° B.115° C.125° D.180°
8.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
9.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
10.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
二、填空题(共10小题)
11.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为 cm.
12.三角形三边长分别为6cm,8cm,10cm,则它的内切圆半径为 cm.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 .
14.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
15.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
16.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD= 度.
17.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
18.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
19.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
20.如图,直线y=﹣x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 .
三、解答题(共10小题)
21.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
23.如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
24.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
25.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
26.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
27.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE
(1)求证:OA=OB;
(2)已知AB=4 ,OA=4,求阴影部分的面积.
28.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
29.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
30.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
求证:(1)AC是⊙D的切线;
(2)AB+EB=AC.
北师大新版九年级(下)《第3章 圆》常考题套卷(3)
参考答案与试题解析
一、选择题(共10小题)
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
【解答】解:连接OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
2.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π B.4π C.12π D.24π
【解答】解:S==12π,
故选:C.
3.如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A. B. C. D.
【解答】解:作AH⊥BC于H,如图,BE=2t,BD=8﹣2t,
∵AB=AC=5,
∴BH=CH=BC=4,
当BE⊥DE,直线DE与⊙O相切,则∠BED=90°,
∵∠EBD=∠ABH,
∴△BED∽△BHA,
∴=,即=,解得t=.
故选:A.
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
5.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
【解答】解:∵点M的坐标是(4,3),
∴点M到x轴的距离是3,到y轴的距离是4,
∵点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,
∴r的取值范围是3<r<4,
故选:D.
6.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,
①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;
②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;
下面有四个结论:
①CD+EF=AB
②
③∠CO2D+∠EO3F=∠AO1B
④∠CDO2+∠EFO3=∠P
所有正确结论的序号是( )
A.①②③④ B.①②③ C.②④ D.②③④
【解答】解:由题意得,AP=CD,BP=EF,
∵AP+BP>AB,
∴CD+EF>AB;
∵⊙O1,⊙O2,⊙O3是等圆,
∴=,=,
∵+=,
∴+=;
∴∠CO2D=∠AO1P,∠EO3F=∠BO1P,
∵∠AO1P+∠BO1P=∠AO1P,
∴∠CO2D+∠EO3F=∠AO1B;
∵∠CDO2=∠APO1,∠BPO1=∠EFO3,
∵∠P=∠APO1+∠BPO1,
∴∠CDO2+∠EFO3=∠P,
∴正确结论的序号是②③④,
故选:D.
7.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为( )
A.90° B.115° C.125° D.180°
【解答】解:本题中弧长应该是10cm,
根据半径为5cm,那么5×π×n÷180=10,
那么圆心角n≈115°.
故选:B.
8.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
【解答】解:设∠BAD=x,则∠BOD=2x,
∵∠BCD=∠BOD=2x,∠BAD+∠BCD=180°,
∴3x=180°,
∴x=60°,
∴∠BAD=60°,
故选:C.
9.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
【解答】解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F,
∵AB,AE都为圆的切线,
∴AE=AB,
∵OB=OE,AO=AO,
∴△ABO≌△AEO(SSS),
∴∠OAB=∠OAE,
∴AO⊥BE,
在直角△AOB里AO2=OB2+AB2,
∵OB=1,AB=3,
∴AO=,
易证明△BOF∽△AOB,
∴BO:AO=OF:OB,
∴1:=OF:1,
∴OF=,
sin∠CBE==,
故选:D.
10.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
【解答】解:如图作PH⊥BC于H.
∵=,
∴∠ACD=∠BCD,
∵BC是直径,
∴∠BAC=90°,
∴PA⊥AC,∵PH⊥BC,
∴PA=PH,设PA=PH=x,
∵PC=PC,
∴Rt△PCA≌Rt△PCH,
∴AC=CH=3,
∵BC==5,
∴BH=2,
在Rt△PBH中,∵PB2=PH2+BH2,
∴(4﹣x)2=x2+22,
解得x=,
∴PC==,
故选:D.
二、填空题(共10小题)
11.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为 18 cm.
【解答】解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2×=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
12.三角形三边长分别为6cm,8cm,10cm,则它的内切圆半径为 2 cm.
【解答】解:如图所示:△ABC中,AC=6,BC=8,AB=10,
∵62+82=102,即AC2+BC2=AB2,
∴△ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵CD=CE,BE=BF,AF=AD,
∵OD⊥AC,OE⊥BC,
∴四边形ODCE是正方形,即CD=CE=R,
∴AC﹣CD=AB﹣BF,即6﹣R=10﹣BF①
BC﹣CE=AB﹣AF,即8﹣R=BF②,
①②联立得,R=2.
故答案为:2.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 6.5cm或2.5cm .
【解答】解:点P应分为位于圆的内部与外部两种情况讨论:
①当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是4+9=13cm,因而半径是6.5cm;
②当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是9﹣4=5cm,因而半径是2.5cm.
故答案为6.5cm或2.5cm.
14.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 6π .
【解答】解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
15.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 28° .
【解答】解:设半圆圆心为O,连OA,OB,如图,
∵∠ACB=∠AOB,
而∠AOB=86°﹣30°=56°,
∴∠ACB=×56°=28°.
故答案为:28°.
16.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD= 10 度.
【解答】解:∵△ABC中,∠ACB=90°,∠A=40°
∴∠B=50°
∵BC=CD
∴∠B=∠BDC=50°
∴∠BCD=80°
∴∠ACD=10°.
17.如图,AB是⊙O的弦,OC⊥AB,垂足为点C,将劣弧沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 3 .
【解答】解:连接OA,设半径为x,
∵将劣弧沿弦AB折叠交于OC的中点D,
∴OC=,OC⊥AB,
∴AC==,
∵OA2﹣OC2=AC2,
∴,
解得,x=3.
故答案为:3.
18.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 2 .
【解答】解:连接OP、OQ,作OP′⊥AB于P′,
∵PQ是⊙O的切线,
∴OQ⊥PQ,
∴PQ==,
当OP最小时,线段PQ的长度最小,
当OP⊥AB时,OP最小,
在Rt△AOB中,∠A=30°,
∴OA==6,
在Rt△AOP′中,∠A=30°,
∴OP′=OA=3,
∴线段PQ长度的最小值==2,
故答案为:2.
19.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
【解答】解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
20.如图,直线y=﹣x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是 (﹣,0)或P(﹣,0) .
【解答】解:∵直线y=﹣x﹣3交x轴于点A,交y轴于点B,
∴令x=0,得y=﹣3,令y=0,得x=﹣4,
∴A(﹣4,0),B(0,﹣3),
∴OA=4,OB=3,
∴AB=5,
设⊙P与直线AB相切于D,
连接PD,
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴=,
∴=,
∴AP=,
∴OP=或OP=,
∴P(﹣,0)或P(﹣,0),
故答案为:(﹣,0)或P(﹣,0).
三、解答题(共10小题)
21.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
【解答】解:∠DAE与∠DAC相等,
理由:∵DB=DC,
∠DBC=∠DCB,
∵∠DAE是四边形ABCD的一个外角,
∴∠EAD=∠DCB,
∴∠DBC=∠EAD,
又∵∠DAC=∠DBC,
∴∠DAE=∠DAC.
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
【解答】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
23.如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
【解答】(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,
∴AD为⊙O的直径,
∴∠AED=90°,
∴∠ACB=∠AED.
∵AD是△ABC中∠BAC的平分线,
∴∠CAD=∠EAD,
∴CD=DE,
在Rt△ACD与Rt△AED中,
,
∴△ACD≌△AED(HL),
∴AC=AE;
(2)∵△ABC是直角三角形,且AC=6,BC=8,
∴AB===10,
∵由(1)得,∠AED=90°,
∴∠BED=90°.
设CD=DE=x,则DB=BC﹣CD=8﹣x,EB=AB﹣AE=10﹣6=4,
在Rt△BED中,根据勾股定理得,BD2=BE2+ED2,即(8﹣x)2=x2+42,解得x=3,
∴CD=3,
∵AC=6,△ACD是直角三角形,
∴AD2=AC2+CD2=62+32=45,
∴AD=3.
解法二:由△BDE∽△BAC,
可得=,可得DE=3,
∴AD===3.
24.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O是AB的中点,
∴S△POB=S△PAB=×AP PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
25.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
【解答】解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
26.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 60° ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
【解答】解:(1)如图1,连接OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°,
∠E的度数为60°;
(2)①如图2,直线AD,CB交于点E,连接OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连接OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
27.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE
(1)求证:OA=OB;
(2)已知AB=4 ,OA=4,求阴影部分的面积.
【解答】解:(1)连接OC,
∵AB与⊙O相切于点C
∴∠ACO=90°,
∵CD=CE
∴=,
∴∠AOC=∠BOC,
∴∠A=∠B
∴OA=OB,
(2)由(1)可知:△OAB是等腰三角形,
∴BC=AB=2,
∴sin∠COB==,
∴∠COB=60°,
∴∠B=30°,
∴OC=OB=2,
∴扇形OCE的面积为:=,
△OCB的面积为:×2×2=2,
S阴影=2﹣π.
28.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
【解答】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:π×132=169π(cm2).
29.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
【解答】解:(1)相切,理由如下:
连接AD,OD,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD∥AC.
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠ODE=∠CED=90°.
∴OD⊥DE.
∴DE与⊙O相切.
(2)由(1)知∠ADC=90°,
∴在Rt△ADC中,由勾股定理 得
AD==4.
∵SACD=AD CD=AC DE,
∴×4×3=×5DE.
∴DE=.
30.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
求证:(1)AC是⊙D的切线;
(2)AB+EB=AC.
【解答】解:(1)过点D作DF⊥AC于F;
∵AB为⊙D的切线,
∴∠B=90°
∴AB⊥BC
∵AD平分∠BAC,DF⊥AC
∴BD=DF
∴AC与⊙D相切;
(2)在△BDE和△DCF中,
∵BD=DF,DE=DC,
在Rt△BDE和Rt△DCF中,
,
∴Rt△BDE≌Rt△DCF(HL),
∴EB=FC.
∵AB=AF,
∴AB+EB=AF+FC,
即AB+EB=AC.
第1页(共3页)
