大题专攻(二) “解三角形”大题的思维建模(共21张PPT)
文档属性
| 名称 | 大题专攻(二) “解三角形”大题的思维建模(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 21:37:33 | ||
图片预览





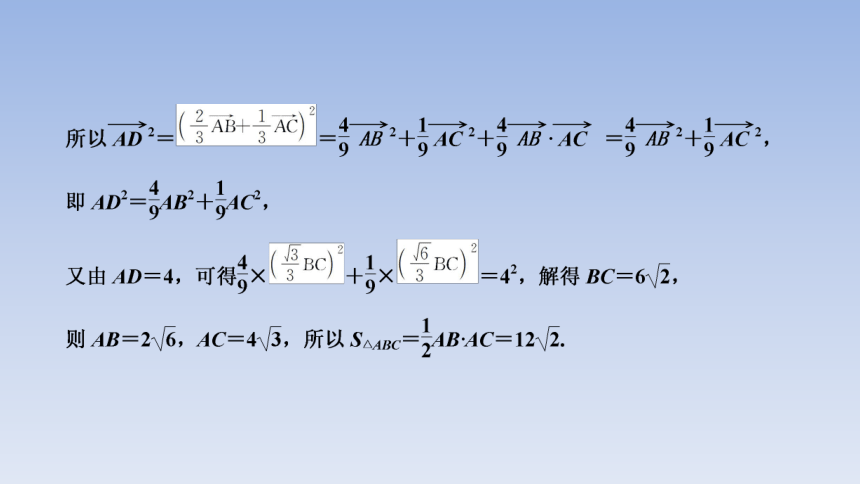
文档简介
(共21张PPT)
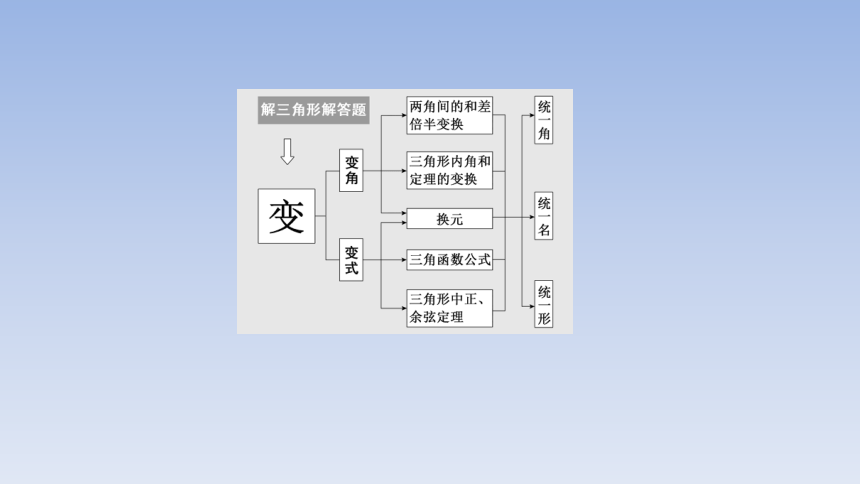
[解题示范]
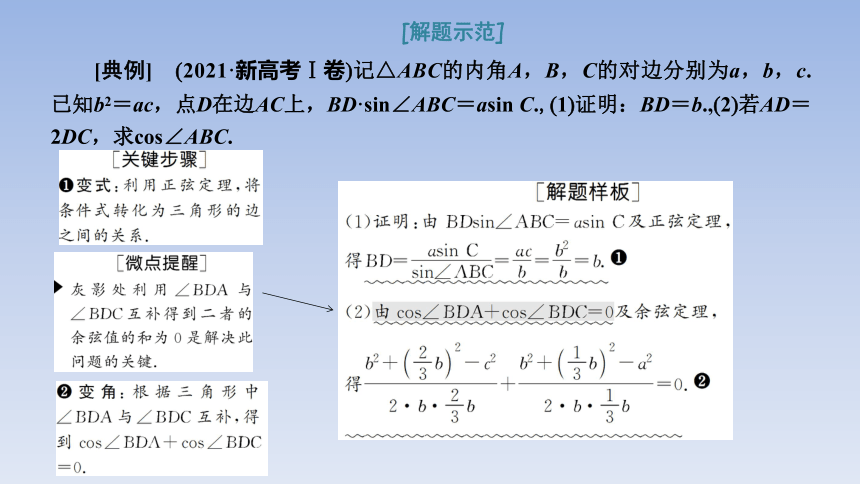
[典例] (2021·新高考Ⅰ卷)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BD·sin∠ABC=asin C.,(1)证明:BD=b.,(2)若AD=2DC,求cos∠ABC.
[关键点拨]
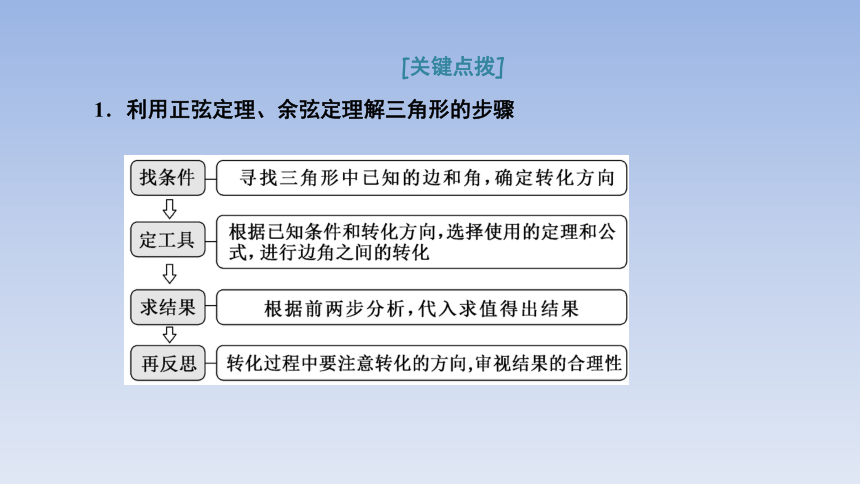
1.利用正弦定理、余弦定理解三角形的步骤
2.解三角形中的注意点
(1)涉及求范围的问题,一定要搞清已知变量的范围,利用已知的范围进行求解,已知边的范围求角的范围时可以利用余弦定理进行转化.
(2)注意题目中的隐含条件,如A+B+C=π,0二 微观优化解题细节:解三角形必须具备的三个意识
“解三角形”的总体难度适中,入手比较容易,但在具体解决问题时,学生易出现“会而不对,对而不全”的情况.主要表现为:公式记忆不准确;在三角函数公式变形中转化不当,导致后续求解复杂或运算错误;忽视三角形中的隐含条件,求边、角时忽略其范围等.
基于以上误区,解决此类问题要强化以下三个意识.
意识一 边角互化
[例1] (2021·新乡二模)a,b,c分别为锐角△ABC内角A,B,C的对边.已知2asin A=(2sin B-sin C)b+(2sin C-sin B)c.
(1)求A;
(2)若c=2,试问b的值是否可能为5?若可能,求△ABC的周长;若不可能,请说明理由.
[反思领悟]
正弦定理、余弦定理应用的主要功能是实现三角形中的边角互化.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的齐次式,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理是否都要应用.正弦定理、余弦定理的灵活应用需深入领会化归与转化思想,需要在解题中多归纳、多总结,抽象概括,总结方法规律.
涉及应用正弦定理、余弦定理的还有一种题型是判断三角形的形状,通常从两个方向进行变形:一个方向是边,考虑代数变形,通常正弦定理、余弦定理结合使用;另一个方向是角,考虑三角变形,通常运用正弦定理.
[反思领悟]
三角函数是一种重要的初等函数,函数与方程是高中数学的重要思想方法之一,在解决解三角形问题时常常用到该思想方法.对于求值或最值问题,也要求学生具有较强的函数与方程意识,构建未知量的函数与方程关系从而解决问题.同时,利用函数、方程、不等式解题时要注意变量范围的限制,要特别注意对一些隐含条件的挖掘,缩小角的取值范围.
[反思领悟]
对于上述问题的解答,应先厘清图形中边、角的关系,将已知条件抽象概括后,一般有两个方向:(1)把已知量全部集中在一个三角形中,利用正弦定理、余弦定理求解;(2)已知量与未知量涉及两个或两个以上三角形,先考虑解条件充分的三角形,再逐步解其他三角形,有时需要设出未知量,从几个三角形中列出方程(组),解方程(组).
[解题示范]
[典例] (2021·新高考Ⅰ卷)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BD·sin∠ABC=asin C.,(1)证明:BD=b.,(2)若AD=2DC,求cos∠ABC.
[关键点拨]
1.利用正弦定理、余弦定理解三角形的步骤
2.解三角形中的注意点
(1)涉及求范围的问题,一定要搞清已知变量的范围,利用已知的范围进行求解,已知边的范围求角的范围时可以利用余弦定理进行转化.
(2)注意题目中的隐含条件,如A+B+C=π,0
“解三角形”的总体难度适中,入手比较容易,但在具体解决问题时,学生易出现“会而不对,对而不全”的情况.主要表现为:公式记忆不准确;在三角函数公式变形中转化不当,导致后续求解复杂或运算错误;忽视三角形中的隐含条件,求边、角时忽略其范围等.
基于以上误区,解决此类问题要强化以下三个意识.
意识一 边角互化
[例1] (2021·新乡二模)a,b,c分别为锐角△ABC内角A,B,C的对边.已知2asin A=(2sin B-sin C)b+(2sin C-sin B)c.
(1)求A;
(2)若c=2,试问b的值是否可能为5?若可能,求△ABC的周长;若不可能,请说明理由.
[反思领悟]
正弦定理、余弦定理应用的主要功能是实现三角形中的边角互化.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的齐次式,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理是否都要应用.正弦定理、余弦定理的灵活应用需深入领会化归与转化思想,需要在解题中多归纳、多总结,抽象概括,总结方法规律.
涉及应用正弦定理、余弦定理的还有一种题型是判断三角形的形状,通常从两个方向进行变形:一个方向是边,考虑代数变形,通常正弦定理、余弦定理结合使用;另一个方向是角,考虑三角变形,通常运用正弦定理.
[反思领悟]
三角函数是一种重要的初等函数,函数与方程是高中数学的重要思想方法之一,在解决解三角形问题时常常用到该思想方法.对于求值或最值问题,也要求学生具有较强的函数与方程意识,构建未知量的函数与方程关系从而解决问题.同时,利用函数、方程、不等式解题时要注意变量范围的限制,要特别注意对一些隐含条件的挖掘,缩小角的取值范围.
[反思领悟]
对于上述问题的解答,应先厘清图形中边、角的关系,将已知条件抽象概括后,一般有两个方向:(1)把已知量全部集中在一个三角形中,利用正弦定理、余弦定理求解;(2)已知量与未知量涉及两个或两个以上三角形,先考虑解条件充分的三角形,再逐步解其他三角形,有时需要设出未知量,从几个三角形中列出方程(组),解方程(组).
同课章节目录
