大题专攻(一) “解三角形”大题的考法研究(22张PPT)
文档属性
| 名称 | 大题专攻(一) “解三角形”大题的考法研究(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 649.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 21:36:34 | ||
图片预览







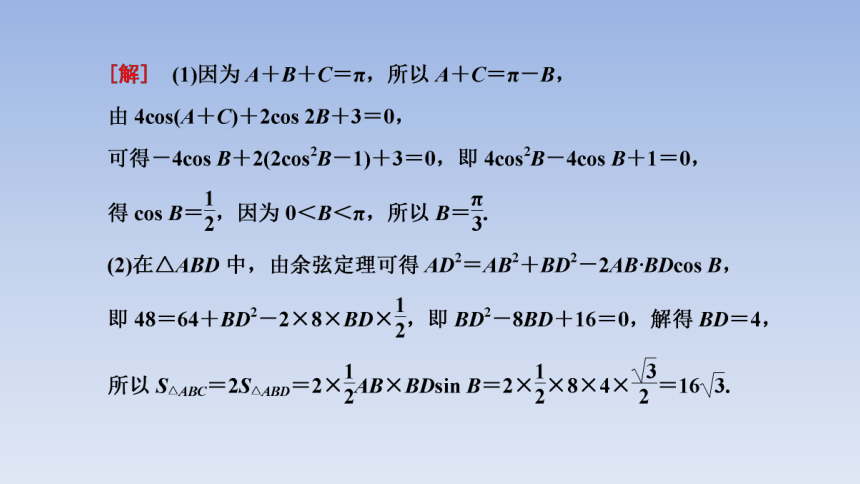

文档简介
(共22张PPT)
切入点 把条件式4cos(A+C)+2cos 2B+3=0化为关于cos B的方程
障碍点 把求△ABC的面积转化为求△ABD的面积问题
隐藏点 A+C=π-B cos(A+C)=-cos B
2.(2021·新高考Ⅱ卷)在△ABC中,角A,B,C所对的边长分别为a,b,c,b=a+1,c=a+2.
(1)若2sin C=3sin A,求△ABC的面积;
(2)是否存在正整数a,使得△ABC为钝角三角形?若存在,求出a的值;若不存在,说明理由.
切入点 把条件式中的cos(B+C)化为-cos A解三角方程求A
障碍点 三角恒等变换
隐藏点 锐角三角形ABC中的三个角都是锐角,由此得到角B或角C的范围,用以求△ABC面积的范围
[提分技巧]
求解与三角形有关的最值或范围问题的方法
利用正、余弦定理等知识求解与三角形有关的最值、范围问题,一般是构造关于某一角或某一边的函数或不等式,再利用函数的单调性或基本不等式等来处理.破解此类题的关键点如下:
定基本量 根据题意或几何图形厘清三角形中的边、角的关系,利用正、余弦定理求出相关的边、角或边角关系,并选择相关的边、角作为基本变量,确定基本变量的变化范围
构建函数 将待求范围的变量,根据正、余弦定理或三角恒等变换转化为基本变量的函数关系式
求最值、范围 利用基本不等式或函数的单调性、有界性等求最值、范围
切入点 把条件式4cos(A+C)+2cos 2B+3=0化为关于cos B的方程
障碍点 把求△ABC的面积转化为求△ABD的面积问题
隐藏点 A+C=π-B cos(A+C)=-cos B
2.(2021·新高考Ⅱ卷)在△ABC中,角A,B,C所对的边长分别为a,b,c,b=a+1,c=a+2.
(1)若2sin C=3sin A,求△ABC的面积;
(2)是否存在正整数a,使得△ABC为钝角三角形?若存在,求出a的值;若不存在,说明理由.
切入点 把条件式中的cos(B+C)化为-cos A解三角方程求A
障碍点 三角恒等变换
隐藏点 锐角三角形ABC中的三个角都是锐角,由此得到角B或角C的范围,用以求△ABC面积的范围
[提分技巧]
求解与三角形有关的最值或范围问题的方法
利用正、余弦定理等知识求解与三角形有关的最值、范围问题,一般是构造关于某一角或某一边的函数或不等式,再利用函数的单调性或基本不等式等来处理.破解此类题的关键点如下:
定基本量 根据题意或几何图形厘清三角形中的边、角的关系,利用正、余弦定理求出相关的边、角或边角关系,并选择相关的边、角作为基本变量,确定基本变量的变化范围
构建函数 将待求范围的变量,根据正、余弦定理或三角恒等变换转化为基本变量的函数关系式
求最值、范围 利用基本不等式或函数的单调性、有界性等求最值、范围
同课章节目录
