特别指导—三角函数中含参数的题型例析(自主研修)(30张PPT)
文档属性
| 名称 | 特别指导—三角函数中含参数的题型例析(自主研修)(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 21:09:55 | ||
图片预览








文档简介
(共30张PPT)
特别指导—三角函数中含参数的题型例析(自主研修)
根据三角函数的相关性质求解参数的值或取值范围是三角函数中比较典型的一类问题,能有效考查学生对三角函数基本性质的掌握程度,难度可控,备受高考命题者的青睐,因此频频出现在高考试题中.这类问题一般涉及值域、单调性及周期性等性质,三角函数因为其函数性质的特殊性,如正弦函数和余弦函数的有界性,往往在确定变量范围,或者最大、最小值有关问题上起着特殊作用.如果试题本身对自变量的取值范围问题有限制,则更应该充分注意.
题型(一) ω的取值范围与单调性相结合
如果解析式中含有参数,要求根据函数单调性求参数的取值范围,通常先求出单调区间,然后利用集合间的关系求解;或转化为使得某个等式或不等式恒(可以)成立,通过分离参数,求出解析式的范围或最值,进而求出参数的范围.
[反思领悟]
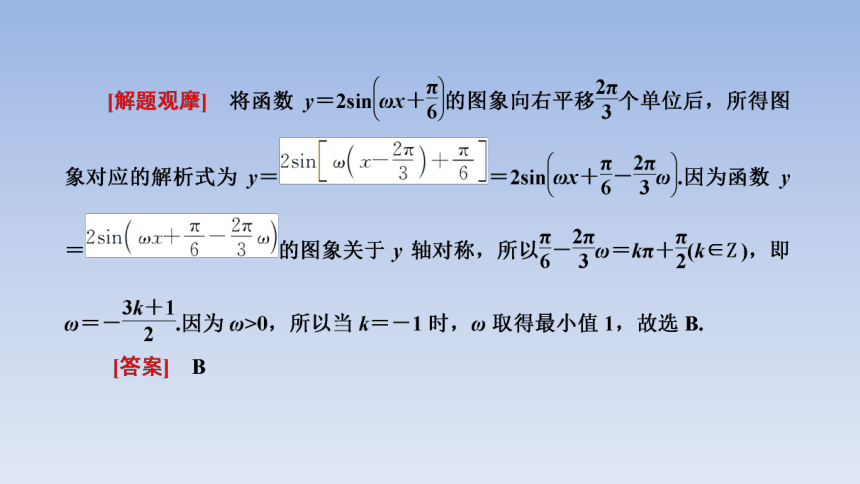
利用三角函数的最值与对称或周期的关系,可以列出关于ω的不等式,进而求出ω的值或取值范围.
[反思领悟]
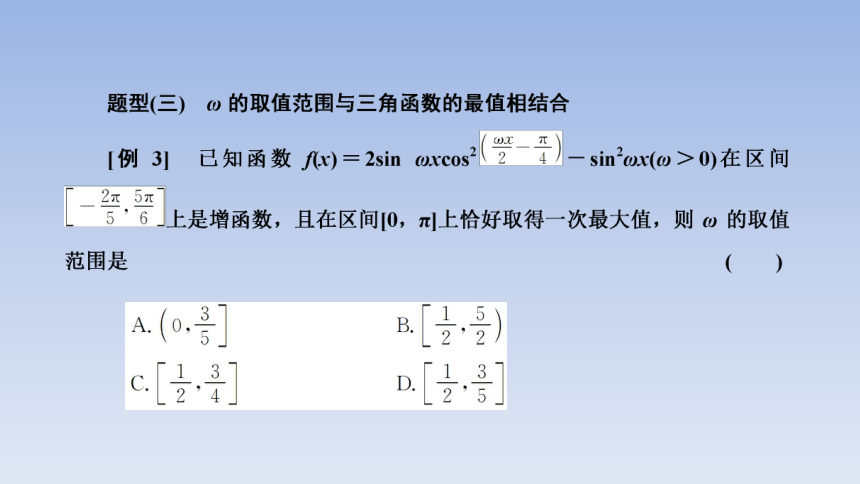
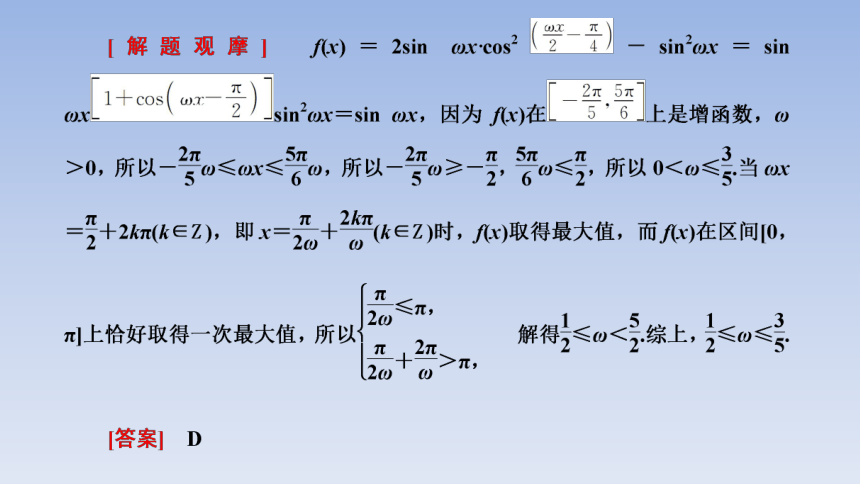
解决此类问题,要先根据所给的单调区间判断ω的大致范围,再计算对称轴,依据函数在所给区间的极值点及对称轴缩小范围,从而求出ω的范围.
.号]
[38)
afy2
[
谢谢观看
特别指导—三角函数中含参数的题型例析(自主研修)
根据三角函数的相关性质求解参数的值或取值范围是三角函数中比较典型的一类问题,能有效考查学生对三角函数基本性质的掌握程度,难度可控,备受高考命题者的青睐,因此频频出现在高考试题中.这类问题一般涉及值域、单调性及周期性等性质,三角函数因为其函数性质的特殊性,如正弦函数和余弦函数的有界性,往往在确定变量范围,或者最大、最小值有关问题上起着特殊作用.如果试题本身对自变量的取值范围问题有限制,则更应该充分注意.
题型(一) ω的取值范围与单调性相结合
如果解析式中含有参数,要求根据函数单调性求参数的取值范围,通常先求出单调区间,然后利用集合间的关系求解;或转化为使得某个等式或不等式恒(可以)成立,通过分离参数,求出解析式的范围或最值,进而求出参数的范围.
[反思领悟]
利用三角函数的最值与对称或周期的关系,可以列出关于ω的不等式,进而求出ω的值或取值范围.
[反思领悟]
解决此类问题,要先根据所给的单调区间判断ω的大致范围,再计算对称轴,依据函数在所给区间的极值点及对称轴缩小范围,从而求出ω的范围.
.号]
[38)
afy2
[
谢谢观看
同课章节目录
