大题专攻(二) “数列”大题的思维建模 课件(共18张PPT)
文档属性
| 名称 | 大题专攻(二) “数列”大题的思维建模 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 750.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:02:00 | ||
图片预览






文档简介
(共18张PPT)
大题专攻(二) “数列”大题的思维建模
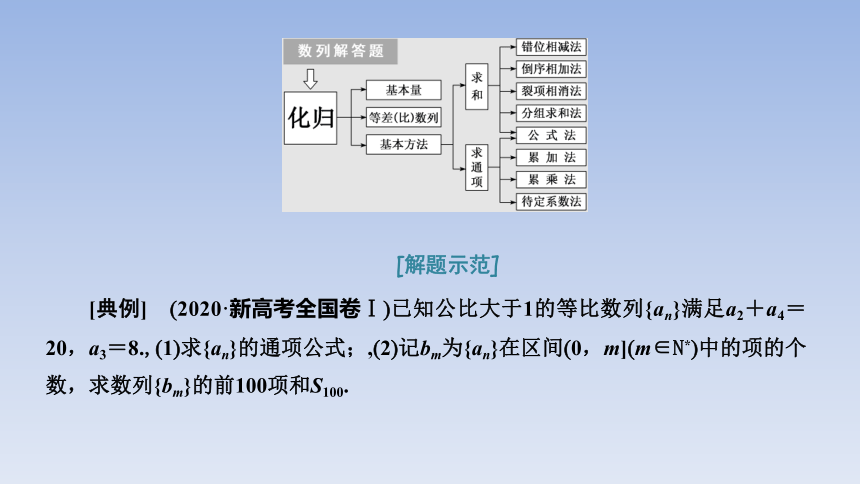
一 宏观掌握解题通路:数列问题重在“归”——化归
等差数列与等比数列是我们最熟悉的两个基本数列,在高中阶段它们是一切数列问题的出发点与落脚点.首项与公差(比)称为等差(比)数列的基本量,大凡涉及这两个数列的问题,我们总希望把已知条件化归为等差或等比数列的基本量间的关系,从而达到解决问题的目的.这种化归为基本量处理的方法是解决等差或等比数列问题特有的方法.对于不是等差或等比的数列,可通过转化化归,转化为等差(比)数列问题或相关问题求解.由于数列是一种特殊的函数,也可根据题目特点,将数列问题化归为函数问题来解决.
[解题示范]
[典例] (2020·新高考全国卷Ⅰ)已知公比大于1的等比数列{an}满足a2+a4=20,a3=8.,(1)求{an}的通项公式;,(2)记bm为{an}在区间(0,m](m∈N*)中的项的个数,求数列{bm}的前100项和S100.
[关键点拨]
1.等差数列、等比数列综合问题的两大解题策略
(1)设置中间问题:求和需要先求出通项,求通项需要先求出首项和公差(公比)等,确定解题的顺序.
(2)注意解题细节:在数列的通项问题中第一项和后面的项能否用同一个公式表示等,这些细节对解题的影响也是巨大的.
2.数列与不等式的综合问题的类型及解题策略
(1)判断数列问题的一些不等关系,可以利用数列的单调性比较大小或借助数列对应的函数的单调性比较大小.
(2)以数列为载体,考查不等式恒成立的问题,此类问题可转化为函数的最值.
(3)考查与数列有关的不等式证明问题,此类问题一般采用放缩法进行证明,有时也可通过构造函数进行证明.
二 微观优化解题细节:数列的“模型化”命题解密
在高中阶段,数列是自变量为正整数的一类特殊函数.高考强调对数列从方程和函数的视角进行研究,其中方程的视角主要体现基础性,即运用等差、等比数列的公式来获得首项、通项公式、公差(比)、前n项和等基本量;函数的视角则体现综合性,主要突出等差数列与一次函数,等比数列与指数函数的关系.高考命题中则强调二次型与等差数列的联系,一次型与等比数列的联系.
大题专攻(二) “数列”大题的思维建模
一 宏观掌握解题通路:数列问题重在“归”——化归
等差数列与等比数列是我们最熟悉的两个基本数列,在高中阶段它们是一切数列问题的出发点与落脚点.首项与公差(比)称为等差(比)数列的基本量,大凡涉及这两个数列的问题,我们总希望把已知条件化归为等差或等比数列的基本量间的关系,从而达到解决问题的目的.这种化归为基本量处理的方法是解决等差或等比数列问题特有的方法.对于不是等差或等比的数列,可通过转化化归,转化为等差(比)数列问题或相关问题求解.由于数列是一种特殊的函数,也可根据题目特点,将数列问题化归为函数问题来解决.
[解题示范]
[典例] (2020·新高考全国卷Ⅰ)已知公比大于1的等比数列{an}满足a2+a4=20,a3=8.,(1)求{an}的通项公式;,(2)记bm为{an}在区间(0,m](m∈N*)中的项的个数,求数列{bm}的前100项和S100.
[关键点拨]
1.等差数列、等比数列综合问题的两大解题策略
(1)设置中间问题:求和需要先求出通项,求通项需要先求出首项和公差(公比)等,确定解题的顺序.
(2)注意解题细节:在数列的通项问题中第一项和后面的项能否用同一个公式表示等,这些细节对解题的影响也是巨大的.
2.数列与不等式的综合问题的类型及解题策略
(1)判断数列问题的一些不等关系,可以利用数列的单调性比较大小或借助数列对应的函数的单调性比较大小.
(2)以数列为载体,考查不等式恒成立的问题,此类问题可转化为函数的最值.
(3)考查与数列有关的不等式证明问题,此类问题一般采用放缩法进行证明,有时也可通过构造函数进行证明.
二 微观优化解题细节:数列的“模型化”命题解密
在高中阶段,数列是自变量为正整数的一类特殊函数.高考强调对数列从方程和函数的视角进行研究,其中方程的视角主要体现基础性,即运用等差、等比数列的公式来获得首项、通项公式、公差(比)、前n项和等基本量;函数的视角则体现综合性,主要突出等差数列与一次函数,等比数列与指数函数的关系.高考命题中则强调二次型与等差数列的联系,一次型与等比数列的联系.
同课章节目录
