大题专攻(三) “概率与统计”大题的思维建模 课件(共25张PPT)
文档属性
| 名称 | 大题专攻(三) “概率与统计”大题的思维建模 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 909.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:06:24 | ||
图片预览






文档简介
(共25张PPT)
大题专攻(三) “概率与统计”大题的思维建模
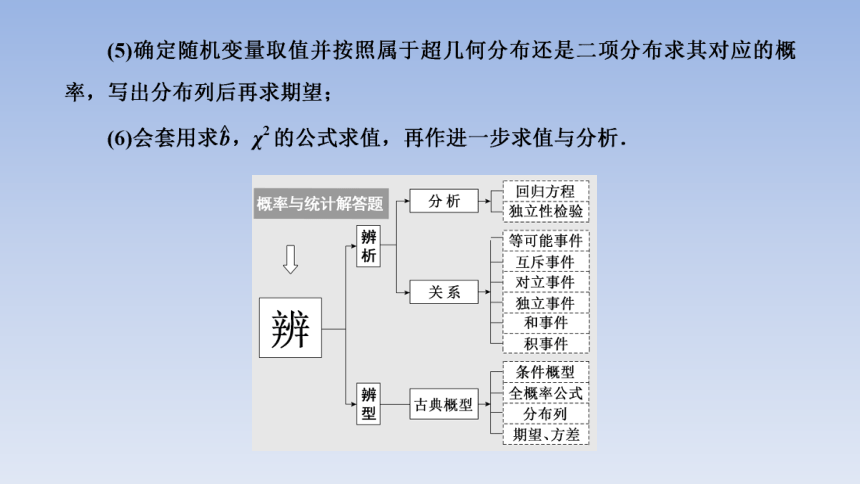
一 宏观掌握解题通路:概率与统计问题重在“辨”——辨析、辨型
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立、独立等;
(2)理清事件以什么形式发生,如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;
(3)明确抽取方式,如放回还是不放回、抽取有无顺序等;
(4)准确选择排列组合的方法来计算样本点个数和样本点总数,或根据概率计算公式和性质来计算事件的概率;
[解题示范]
[典例] (2021·新高考Ⅰ卷)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
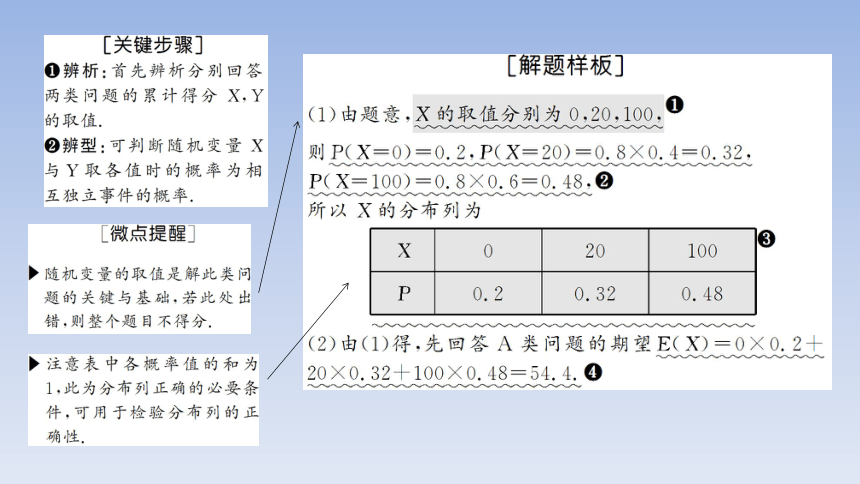
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列.
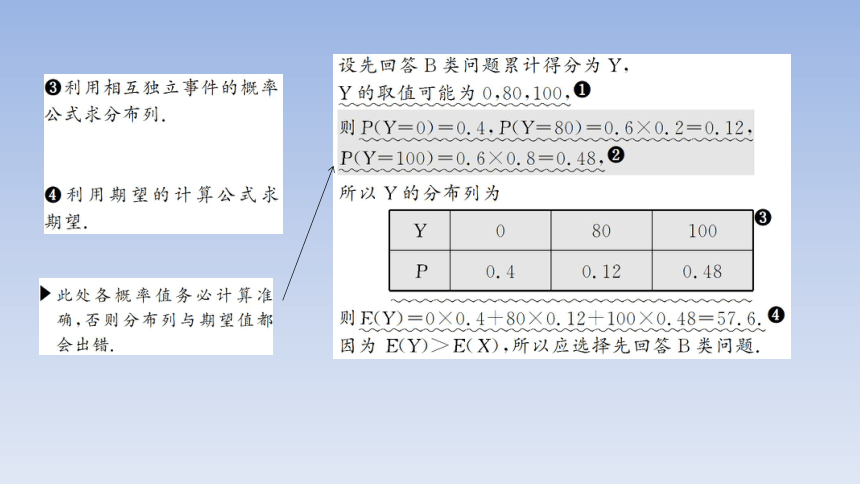
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?说明理由.
[关键点拨]
特征数据法解决决策性问题的策略
特征数据法,就是根据提取的数据,建立相应的概率模型,然后利用概率知识求出决策方案中的特征数值——概率、期望或方差等,通过特征数值的比较得到最优方案,从而解决问题的方法.破解此类问题的关键点如下:
(1)建模型,即根据题意准确建立解决问题的模型,要注意各种模型的差异性,不能混淆;
(2)析数据,即分析题中的相关数据,确定模型中的相关参数;
(3)求特征值,利用概率知识求出模型中随机变量的期望或方差等特征数值;
(4)做决策,比较模型中的特征数值,确定解决问题的最优方案,进而做出决策.
二 微观优化解题细节:三招突破概率、统计大题的解题瓶颈
技法一 信息巧提取
[例1] (2021·佛山开学摸底)高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统计,某一年乘坐高铁或飞机从A市到B市的成年人约50万人次,为了解乘客出行的满意度,现从中随机抽取了100人次作为样本,得到下表(单位:人次).
老年人 中年人 青年人
满意度 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机
10分(满意) 12 1 20 2 20 1
5分(一般) 2 3 6 2 4 9
0分(不满意) 1 0 6 3 4 4
(1)在样本中任取1个,求这个出行人恰好不是青年人的概率.
(2)从这一年乘坐高铁从A市到B市的所有成年人中,随机选取2人次,记其中老年人出行的人次为X,以频率作为概率,求X的分布列和数学期望.
(3)如果甲将要从A市出发到B市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机?并说明理由.
[技法点拨] 此类问题文字叙述较长,解答问题应快速锁定有效信息,其技巧是:①快速了解“无关信息”;②仔细阅读题中重要信息,把握信息所给内容(如本例数字、字母等);③明确题目所求内容.
如本题(2)问中,可将“随机选取1人次,此人次为老年人”视为事件A,则随机选取2人次相当于2重伯努利试验.X表示事件A发生的次数,故X服从二项分布.
技法二 数据巧处理
[例2] 某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 2011 2013 2015 2017 2019
需求量/万吨 236 246 257 276 286
[解题观摩] (1)由所给数据得出,年需求量与年份之间是近似直线上升的关系,下面来配回归直线方程,为此对数据处理如下:
年份-2015 -4 -2 0 2 4
需求量-257 -21 -11 0 19 29
技法三 公式巧变形
[例3] 下图是我国2013年至2019年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1~7分别对应年份2013~2019.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以
说明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2021年我国生活垃圾无害化处理量.
大题专攻(三) “概率与统计”大题的思维建模
一 宏观掌握解题通路:概率与统计问题重在“辨”——辨析、辨型
(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立、独立等;
(2)理清事件以什么形式发生,如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;
(3)明确抽取方式,如放回还是不放回、抽取有无顺序等;
(4)准确选择排列组合的方法来计算样本点个数和样本点总数,或根据概率计算公式和性质来计算事件的概率;
[解题示范]
[典例] (2021·新高考Ⅰ卷)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列.
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?说明理由.
[关键点拨]
特征数据法解决决策性问题的策略
特征数据法,就是根据提取的数据,建立相应的概率模型,然后利用概率知识求出决策方案中的特征数值——概率、期望或方差等,通过特征数值的比较得到最优方案,从而解决问题的方法.破解此类问题的关键点如下:
(1)建模型,即根据题意准确建立解决问题的模型,要注意各种模型的差异性,不能混淆;
(2)析数据,即分析题中的相关数据,确定模型中的相关参数;
(3)求特征值,利用概率知识求出模型中随机变量的期望或方差等特征数值;
(4)做决策,比较模型中的特征数值,确定解决问题的最优方案,进而做出决策.
二 微观优化解题细节:三招突破概率、统计大题的解题瓶颈
技法一 信息巧提取
[例1] (2021·佛山开学摸底)高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统计,某一年乘坐高铁或飞机从A市到B市的成年人约50万人次,为了解乘客出行的满意度,现从中随机抽取了100人次作为样本,得到下表(单位:人次).
老年人 中年人 青年人
满意度 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机
10分(满意) 12 1 20 2 20 1
5分(一般) 2 3 6 2 4 9
0分(不满意) 1 0 6 3 4 4
(1)在样本中任取1个,求这个出行人恰好不是青年人的概率.
(2)从这一年乘坐高铁从A市到B市的所有成年人中,随机选取2人次,记其中老年人出行的人次为X,以频率作为概率,求X的分布列和数学期望.
(3)如果甲将要从A市出发到B市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机?并说明理由.
[技法点拨] 此类问题文字叙述较长,解答问题应快速锁定有效信息,其技巧是:①快速了解“无关信息”;②仔细阅读题中重要信息,把握信息所给内容(如本例数字、字母等);③明确题目所求内容.
如本题(2)问中,可将“随机选取1人次,此人次为老年人”视为事件A,则随机选取2人次相当于2重伯努利试验.X表示事件A发生的次数,故X服从二项分布.
技法二 数据巧处理
[例2] 某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 2011 2013 2015 2017 2019
需求量/万吨 236 246 257 276 286
[解题观摩] (1)由所给数据得出,年需求量与年份之间是近似直线上升的关系,下面来配回归直线方程,为此对数据处理如下:
年份-2015 -4 -2 0 2 4
需求量-257 -21 -11 0 19 29
技法三 公式巧变形
[例3] 下图是我国2013年至2019年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1~7分别对应年份2013~2019.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以
说明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2021年我国生活垃圾无害化处理量.
同课章节目录
