大题专攻(三) “解析几何”压轴大题的思维建模 课件(共24张PPT)
文档属性
| 名称 | 大题专攻(三) “解析几何”压轴大题的思维建模 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:06:58 | ||
图片预览








文档简介
(共24张PPT)
大题专攻(三) “解析几何”压轴大题的思维建模
一 宏观掌握解题通路:解析几何问题巧在“设”,难在“算”
解析几何解答题的常见类型是:第(1)小题通常是根据已知条件,求曲线方程或离心率,一般比较简单.第(2)小题往往是通过方程研究曲线的性质——弦长问题、中点弦问题、动点轨迹问题、定点与定值问题、最值问题、相关量的取值范围问题等等,这一小题综合性较强,可通过巧设“点”“线”,设而不求.在具体求解时,可将整个解题过程分成程序化的三步:
第一步,联立两个方程,并将消元所得方程的判别式与根与系数的关系正确写出;
第二步,用两个交点的同一类坐标的和与积,来表示题目中涉及的位置关系和数量关系;
第三步,求解转化而来的代数问题,并将结果回归到原几何问题中.
在求解时,要根据题目特征,恰当地设点、设线,选用恰当运算方法,合理地简化运算.
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
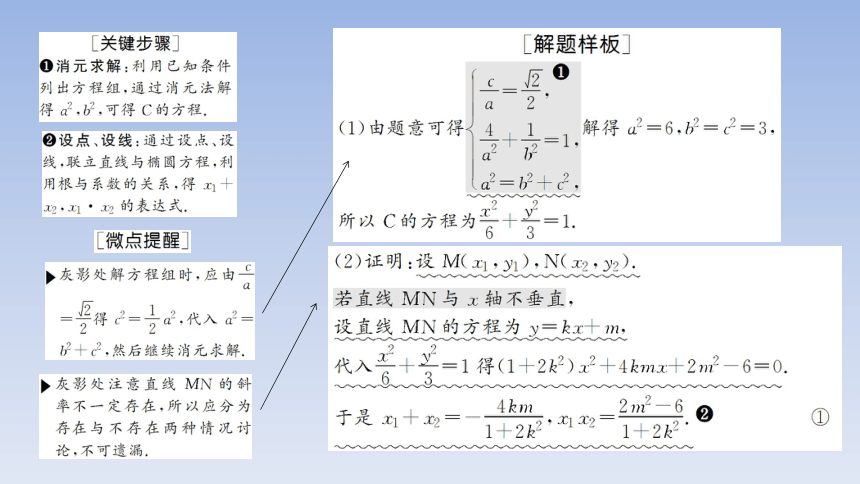
[解题示范]
[典例] (2020·新高考全国卷Ⅰ)已知椭圆 的离心率为 ,且过点A(2,1).
(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
二 微观优化解题细节:合理设参,把握先机
平面解析几何中的许多问题,若解题方法不对就会使解题过程繁杂而冗长,从而影响到解题的速度和解题的准确性,通过引入参数,设而不求是解决此类问题的有效方法.
一旦合理引入参数,用参数来刻画运动变化状态,减少变量,再利用平面几何知识就会化难为易,化繁为简,收到意想不到的解题效果.设参方式一般有以下几种类型:
[反思领悟]
对于圆锥曲线中的双参数问题,在求参数的取值范围时,许多情况下要先根据问题特征,求出其中一个参数的范围,然后寻找两参数的等量关系,借助这个等量关系求另一个参数的范围.
[反思领悟]
“点参”解题是解析几何大题的一种重要方法,尤其在以抛物线为背景的解析几何大题中运用较多.这是因为抛物线方程本身就是一个“x”与“y”的等量关系式,“x”与“y”的转换方便,且有降幂升幂的功能.当然,椭圆背景的大题,也不乏适合“点参”解题的题目.
大题专攻(三) “解析几何”压轴大题的思维建模
一 宏观掌握解题通路:解析几何问题巧在“设”,难在“算”
解析几何解答题的常见类型是:第(1)小题通常是根据已知条件,求曲线方程或离心率,一般比较简单.第(2)小题往往是通过方程研究曲线的性质——弦长问题、中点弦问题、动点轨迹问题、定点与定值问题、最值问题、相关量的取值范围问题等等,这一小题综合性较强,可通过巧设“点”“线”,设而不求.在具体求解时,可将整个解题过程分成程序化的三步:
第一步,联立两个方程,并将消元所得方程的判别式与根与系数的关系正确写出;
第二步,用两个交点的同一类坐标的和与积,来表示题目中涉及的位置关系和数量关系;
第三步,求解转化而来的代数问题,并将结果回归到原几何问题中.
在求解时,要根据题目特征,恰当地设点、设线,选用恰当运算方法,合理地简化运算.
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
[解题示范]
[典例] (2020·新高考全国卷Ⅰ)已知椭圆 的离心率为 ,且过点A(2,1).
(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
二 微观优化解题细节:合理设参,把握先机
平面解析几何中的许多问题,若解题方法不对就会使解题过程繁杂而冗长,从而影响到解题的速度和解题的准确性,通过引入参数,设而不求是解决此类问题的有效方法.
一旦合理引入参数,用参数来刻画运动变化状态,减少变量,再利用平面几何知识就会化难为易,化繁为简,收到意想不到的解题效果.设参方式一般有以下几种类型:
[反思领悟]
对于圆锥曲线中的双参数问题,在求参数的取值范围时,许多情况下要先根据问题特征,求出其中一个参数的范围,然后寻找两参数的等量关系,借助这个等量关系求另一个参数的范围.
[反思领悟]
“点参”解题是解析几何大题的一种重要方法,尤其在以抛物线为背景的解析几何大题中运用较多.这是因为抛物线方程本身就是一个“x”与“y”的等量关系式,“x”与“y”的转换方便,且有降幂升幂的功能.当然,椭圆背景的大题,也不乏适合“点参”解题的题目.
同课章节目录
