大题专攻(三) “立体几何”大题的思维建模 课件(共34张PPT)
文档属性
| 名称 | 大题专攻(三) “立体几何”大题的思维建模 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:07:33 | ||
图片预览










文档简介
(共34张PPT)
大题专攻(三) “立体几何”大题的思维建模
一 宏观掌握解题通路:立体几何问题重在“建”——建模、建系
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深.解决这类题目的原则是建模、建系.
建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型,有时也需建立函数模型;
建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
[解题示范]
(2021·新高考Ⅰ卷)如图,在三棱锥A -BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD.
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,
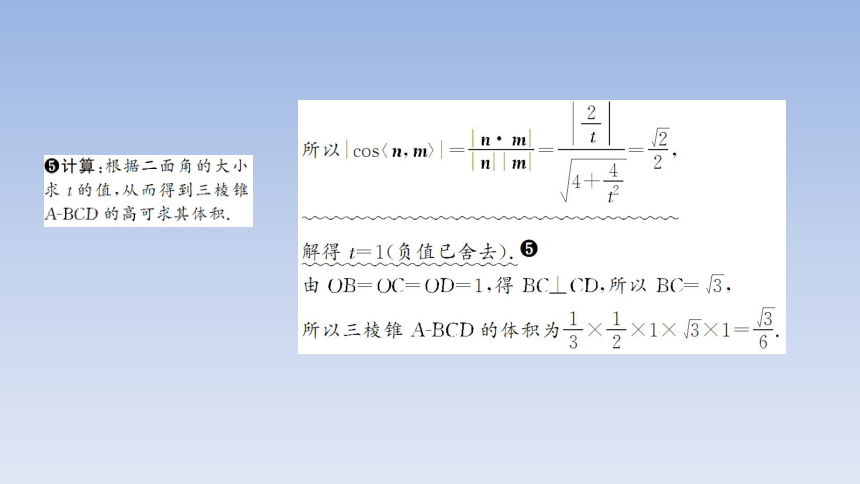
DE=2EA,且二面角E BC D的大小为45°,求三棱锥A BCD的体积.
[关键点拨]
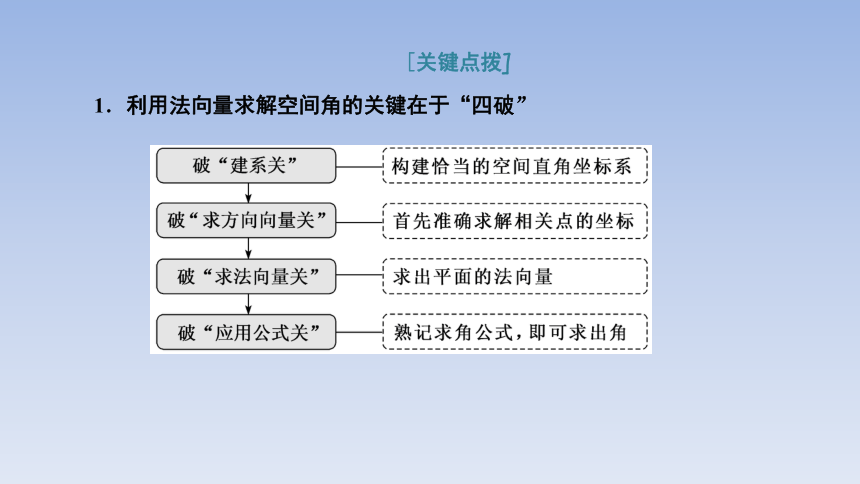
1.利用法向量求解空间角的关键在于“四破”
2.解答立体几何问题,应具备以下5点思维
(1)由于空间图形问题往往可转化为平面图形问题加以解决,因此要注意平面几何知识在解题中的灵活运用.例如,证线线平行可以利用三角形、梯形的中位线性质定理,还可以利用比例关系;证线线垂直可以利用菱形、正方形的对角线互相垂直,还可以利用勾股定理的逆定理.
(2)立体几何中证明有关平行或垂直问题时,由于大多数问题主要考查的是有关判定定理在证题中的灵活运用,所以我们要优先考虑对应的判定定理去寻找证题思路.
(3)立体几何中证明有关平行或垂直问题时,若对应的判定定理不便于运用,则应该及时考虑其他的证题思路.例如,要证线面平行,可以先证面面平行,再利用面面平行的性质;要证明线面垂直,可以先证面面垂直,再利用面面垂直的性质.
(4)分析、解决有关立体几何问题时,往往需要考虑数形结合思想、分类与整合思想、转化思想在解题中的灵活应用.
(5)由于立体几何解答题侧重考查空间向量法在解题中的灵活运用,所以必须熟练掌握利用空间向量法求解空间角的具体过程.
二 微观优化解题细节:提升五大能力,突破立体几何中的解题障碍点
能力一 提高识图、作图能力
识图、作图能力是学好立体几何应具备的重要能力之一,学生的识图、作图能力弱主要集中在作图问题、球问题的直观呈现和转化、展折问题的图形分析等.要提高识图、作图能力,需要理解作图的原理,在此基础上,培养模型意识和动手能力
[反思领悟]
本题往往会因为对直径认识不足(球心O为SC的中点),而纠结如何作图(球内接三棱锥S-ABC),不懂得对问题进行转化(VS-ABC=2VO-ABC),只有正确理解才能把问题转化为三棱锥O-ABC,再结合球的定义即可解决.
[反思领悟]
解答本题的最大障碍是不会过顶点A作出平面α,解决的方法是通过“补体”快速实现把平面CB1D1“外移”,观察和作出平行线是本题作图的关键,常用的方法有利用中位线或平行四边形的性质等,尤其要注意长方体中的一些常见的平行关系(如本题D2B2∥CB1,AD2∥D1B1,AB2∥CD1)和垂直关系,以增加作图的方向感.
能力二 厘清相关概念
数学概念是思考问题、解决问题的出发点,很多同学由于概念意识不强,无法快速地把概念文本转化为相应的空间几何体,易把“异面直线所成的角”与“向量的夹角”混淆,易把“线面所成的角”等同“直线与平面法向量的夹角”,易分辨不清“二面角的平面角”与“两个法向量的夹角”之间的差异,同时对“线面所成的角”或“二面角的平面角”易忽视其定义的本质(即“找、证、算”),而陷入盲目的计算,使得问题复杂化.
[例3] 如图,已知四棱锥P ABCD中,平面PAB⊥平面ABCD,
△PAB为等边三角形,底面ABCD为直角梯形,∠DAB=90°且AB
=2CD,点M在PB上.
(1)若M为PB的中点,求证:DM⊥PB;
(2)若AD=CD,二面角M AD C为30°,求直线DM与平面PBC所成角的余弦值.
[解题观摩] (1)证明:∵△PAB为等边三角形,M为PB的中点,∴AM⊥PB.
又∵平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,DA⊥AB,DA 平面ABCD,∴DA⊥平面PAB,
又PB 平面PAB,∴DA⊥PB,
[反思领悟]
解决本题第(2)问的关键在于厘清二面角M- AD -C与二面角M- AD -C的平面角,只有厘清哪个是平面角,才能寻求坐标之间的关系,在确定∠MAB为二面角的平面角时,要注意应用第(1)问的结论,这也是立体几何解答题的特点之一.事实上,在二面角的平面角的意义中,必须紧扣“相交棱”“两垂直于棱的相交直线”,这往往需要利用“作、证”“相交棱垂直于平面”等知识.
能力三 规范推理步骤
在证明线、面的平行或垂直关系时,由于定理条件掌握不全,推理的逻辑欠规范,常造成“会而不全”,导致失分.如,学生在使用直线与平面平行的判定定理时,常常遗忘“已知直线一定要在该平面外”这个关键的条件;在使用直线与平面垂直的判定定理时,常常遗忘“线不在多,重在相交”这个关键的条件.符号书写也不规范,如,直线与平面是包含与不包含的关系,却常误写成属于与不属于的关系等.
∴MO∥ED,且MO=ED,
∴四边形EDOM是平行四边形,∴EM∥DO,
∵EM 平面ABCD,DO 平面ABCD,∴EM∥平面ABCD.
(2)证明:∵ED∥FC,ED⊥平面ABCD,∴CF⊥平面ABCD.
又∵DO 平面ABCD,∴CF⊥DO,
∵AC⊥DO,CF 平面FAC,AC 平面FAC,CF∩AC=C,
∴DO⊥平面FAC.
由(1)知EM∥DO,∴EM⊥平面FAC.
又∵EM 平面AEF,∴平面AEF⊥平面FAC.
[反思领悟]
(1)要证线面平行,一般可考虑线线平行或面面平行,本题可优
先考虑线线平行,思路较为直接.如图,连接AC,BD,AC∩BD=
O,则O为AC的中点,连接OM,构建平行四边形EDOM.但学生常
常会“想当然”,容易借助几何直观默认EM∥DO,忽视“EDOM
是平行四边形”的证明过程;此外更常忽略条件“EM 平面ABCD,DO 平面ABCD”的完整表达而造成不必要的丢分!
(2)要证面面垂直,关键在于找出一组“线面垂直”,如图,能较为直观看到“EM⊥平面FAC”就是目标.证明过程中常因几何直观强,而忽视平行关系与垂直关系之间的转化,直接“想当然”“易得CF⊥EM,AC⊥EM”造成失分,同时条件“EM 平面AEF”也是学生证明面面垂直最容易丢分的地方.
能力四 建立适当的坐标系
利用向量法求空间角是高考的必考试题,由于有些考题所给的几何体不规则,造成建系困难或建系不合理,也常出现“没有证明三线两两垂直”就“想当然”建系等错误.
[例5] (2015·全国卷Ⅰ)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
[反思领悟]
本题主要考查立体几何的线面、面面位置关系,考查推理论证能力、运算求解能力、空间想象能力.由于几何体给人感觉不规则,第(2)问利用几何法不易求解,建系也比较困难.学生的主要失误点是:一是没有建好坐标系,被“图”迷惑了双眼,一下子盯住点B,D,把点B或点D视为空间直角坐标系的原点导致解题难度增加,易失分;二是贪快,导致图形中的坐标系漏画,例如,如图建立空间直角坐标系,但图中是空的;三是空间直角坐标系建成左手系,而不是建成右手系,建成左手系算错,丢分太可惜.事实上,建立合理的坐标系是代数法解立体几何题的关键.建立坐标系就是构造(或寻找)三线两两垂直,可分步处理,
能力五 提高运算能力
在解决立体几何中涉及求几何体的表面积、体积以及求角度等问题时,运算性的错误也很常见,主要表现在:①错用几何体的表面积、体积公式;②错选向量或向量公式求解相关问题;③运算过程因粗心致错等.这就要求我们在平时学习过程中运算要仔细,不要跳步,养成良好的运算习惯,有意识地提高运算能力.
大题专攻(三) “立体几何”大题的思维建模
一 宏观掌握解题通路:立体几何问题重在“建”——建模、建系
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深.解决这类题目的原则是建模、建系.
建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型,有时也需建立函数模型;
建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
[解题示范]
(2021·新高考Ⅰ卷)如图,在三棱锥A -BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD.
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,
DE=2EA,且二面角E BC D的大小为45°,求三棱锥A BCD的体积.
[关键点拨]
1.利用法向量求解空间角的关键在于“四破”
2.解答立体几何问题,应具备以下5点思维
(1)由于空间图形问题往往可转化为平面图形问题加以解决,因此要注意平面几何知识在解题中的灵活运用.例如,证线线平行可以利用三角形、梯形的中位线性质定理,还可以利用比例关系;证线线垂直可以利用菱形、正方形的对角线互相垂直,还可以利用勾股定理的逆定理.
(2)立体几何中证明有关平行或垂直问题时,由于大多数问题主要考查的是有关判定定理在证题中的灵活运用,所以我们要优先考虑对应的判定定理去寻找证题思路.
(3)立体几何中证明有关平行或垂直问题时,若对应的判定定理不便于运用,则应该及时考虑其他的证题思路.例如,要证线面平行,可以先证面面平行,再利用面面平行的性质;要证明线面垂直,可以先证面面垂直,再利用面面垂直的性质.
(4)分析、解决有关立体几何问题时,往往需要考虑数形结合思想、分类与整合思想、转化思想在解题中的灵活应用.
(5)由于立体几何解答题侧重考查空间向量法在解题中的灵活运用,所以必须熟练掌握利用空间向量法求解空间角的具体过程.
二 微观优化解题细节:提升五大能力,突破立体几何中的解题障碍点
能力一 提高识图、作图能力
识图、作图能力是学好立体几何应具备的重要能力之一,学生的识图、作图能力弱主要集中在作图问题、球问题的直观呈现和转化、展折问题的图形分析等.要提高识图、作图能力,需要理解作图的原理,在此基础上,培养模型意识和动手能力
[反思领悟]
本题往往会因为对直径认识不足(球心O为SC的中点),而纠结如何作图(球内接三棱锥S-ABC),不懂得对问题进行转化(VS-ABC=2VO-ABC),只有正确理解才能把问题转化为三棱锥O-ABC,再结合球的定义即可解决.
[反思领悟]
解答本题的最大障碍是不会过顶点A作出平面α,解决的方法是通过“补体”快速实现把平面CB1D1“外移”,观察和作出平行线是本题作图的关键,常用的方法有利用中位线或平行四边形的性质等,尤其要注意长方体中的一些常见的平行关系(如本题D2B2∥CB1,AD2∥D1B1,AB2∥CD1)和垂直关系,以增加作图的方向感.
能力二 厘清相关概念
数学概念是思考问题、解决问题的出发点,很多同学由于概念意识不强,无法快速地把概念文本转化为相应的空间几何体,易把“异面直线所成的角”与“向量的夹角”混淆,易把“线面所成的角”等同“直线与平面法向量的夹角”,易分辨不清“二面角的平面角”与“两个法向量的夹角”之间的差异,同时对“线面所成的角”或“二面角的平面角”易忽视其定义的本质(即“找、证、算”),而陷入盲目的计算,使得问题复杂化.
[例3] 如图,已知四棱锥P ABCD中,平面PAB⊥平面ABCD,
△PAB为等边三角形,底面ABCD为直角梯形,∠DAB=90°且AB
=2CD,点M在PB上.
(1)若M为PB的中点,求证:DM⊥PB;
(2)若AD=CD,二面角M AD C为30°,求直线DM与平面PBC所成角的余弦值.
[解题观摩] (1)证明:∵△PAB为等边三角形,M为PB的中点,∴AM⊥PB.
又∵平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,DA⊥AB,DA 平面ABCD,∴DA⊥平面PAB,
又PB 平面PAB,∴DA⊥PB,
[反思领悟]
解决本题第(2)问的关键在于厘清二面角M- AD -C与二面角M- AD -C的平面角,只有厘清哪个是平面角,才能寻求坐标之间的关系,在确定∠MAB为二面角的平面角时,要注意应用第(1)问的结论,这也是立体几何解答题的特点之一.事实上,在二面角的平面角的意义中,必须紧扣“相交棱”“两垂直于棱的相交直线”,这往往需要利用“作、证”“相交棱垂直于平面”等知识.
能力三 规范推理步骤
在证明线、面的平行或垂直关系时,由于定理条件掌握不全,推理的逻辑欠规范,常造成“会而不全”,导致失分.如,学生在使用直线与平面平行的判定定理时,常常遗忘“已知直线一定要在该平面外”这个关键的条件;在使用直线与平面垂直的判定定理时,常常遗忘“线不在多,重在相交”这个关键的条件.符号书写也不规范,如,直线与平面是包含与不包含的关系,却常误写成属于与不属于的关系等.
∴MO∥ED,且MO=ED,
∴四边形EDOM是平行四边形,∴EM∥DO,
∵EM 平面ABCD,DO 平面ABCD,∴EM∥平面ABCD.
(2)证明:∵ED∥FC,ED⊥平面ABCD,∴CF⊥平面ABCD.
又∵DO 平面ABCD,∴CF⊥DO,
∵AC⊥DO,CF 平面FAC,AC 平面FAC,CF∩AC=C,
∴DO⊥平面FAC.
由(1)知EM∥DO,∴EM⊥平面FAC.
又∵EM 平面AEF,∴平面AEF⊥平面FAC.
[反思领悟]
(1)要证线面平行,一般可考虑线线平行或面面平行,本题可优
先考虑线线平行,思路较为直接.如图,连接AC,BD,AC∩BD=
O,则O为AC的中点,连接OM,构建平行四边形EDOM.但学生常
常会“想当然”,容易借助几何直观默认EM∥DO,忽视“EDOM
是平行四边形”的证明过程;此外更常忽略条件“EM 平面ABCD,DO 平面ABCD”的完整表达而造成不必要的丢分!
(2)要证面面垂直,关键在于找出一组“线面垂直”,如图,能较为直观看到“EM⊥平面FAC”就是目标.证明过程中常因几何直观强,而忽视平行关系与垂直关系之间的转化,直接“想当然”“易得CF⊥EM,AC⊥EM”造成失分,同时条件“EM 平面AEF”也是学生证明面面垂直最容易丢分的地方.
能力四 建立适当的坐标系
利用向量法求空间角是高考的必考试题,由于有些考题所给的几何体不规则,造成建系困难或建系不合理,也常出现“没有证明三线两两垂直”就“想当然”建系等错误.
[例5] (2015·全国卷Ⅰ)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
[反思领悟]
本题主要考查立体几何的线面、面面位置关系,考查推理论证能力、运算求解能力、空间想象能力.由于几何体给人感觉不规则,第(2)问利用几何法不易求解,建系也比较困难.学生的主要失误点是:一是没有建好坐标系,被“图”迷惑了双眼,一下子盯住点B,D,把点B或点D视为空间直角坐标系的原点导致解题难度增加,易失分;二是贪快,导致图形中的坐标系漏画,例如,如图建立空间直角坐标系,但图中是空的;三是空间直角坐标系建成左手系,而不是建成右手系,建成左手系算错,丢分太可惜.事实上,建立合理的坐标系是代数法解立体几何题的关键.建立坐标系就是构造(或寻找)三线两两垂直,可分步处理,
能力五 提高运算能力
在解决立体几何中涉及求几何体的表面积、体积以及求角度等问题时,运算性的错误也很常见,主要表现在:①错用几何体的表面积、体积公式;②错选向量或向量公式求解相关问题;③运算过程因粗心致错等.这就要求我们在平时学习过程中运算要仔细,不要跳步,养成良好的运算习惯,有意识地提高运算能力.
同课章节目录
