大题专攻(一) 统计、统计案例 课件(共40张PPT)
文档属性
| 名称 | 大题专攻(一) 统计、统计案例 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:10:11 | ||
图片预览


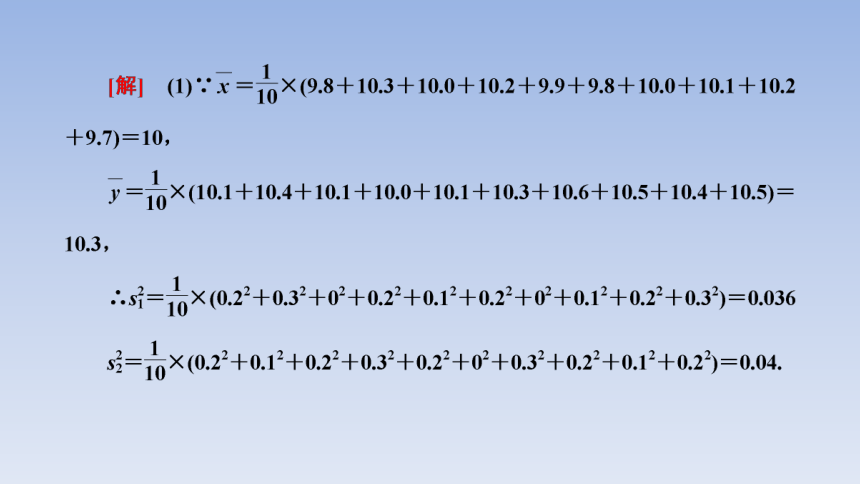






文档简介
(共40张PPT)
大题专攻(一) 统计、统计案例
用样本估计总体
[典例] (2021·全国乙卷)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
[提分技巧]
利用样本的数字特征解决优化决策问题的依据
(1)平均数反映了数据取值的平均水平;标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大,越不稳定;标准差、方差越小,数据的离散程度越小,越稳定.
(2)用样本估计总体就是利用样本的数字特征来描述总体的数字特征.
[对点训练]
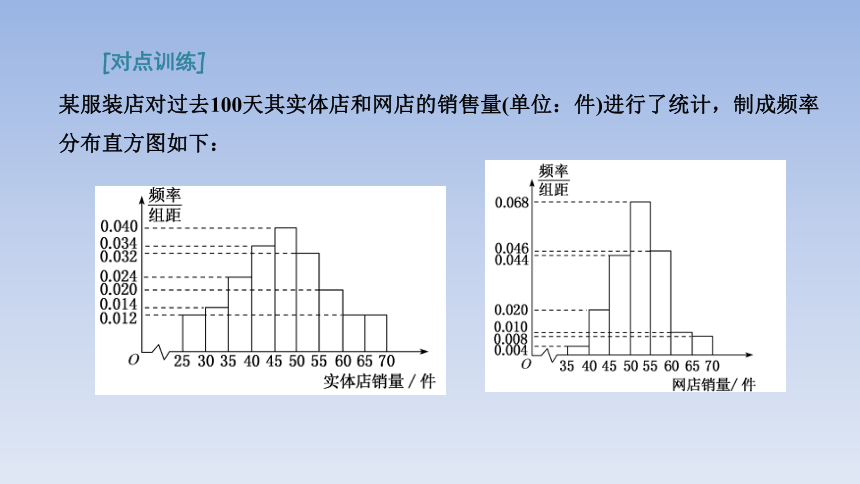
某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50的概率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1 200元,每售出一件利润为50元,求该实体店一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量的中位数的估计值(精确到0.01).
解:(1)由题意知,网店销售量不低于50共有(0.068+0.046+0.010+0.008)×5×100=66(天),实体店销售量不低于50共有(0.032+0.020+0.012×2)×5×100=38(天),实体店和网店销售量都不低于50的天数为100×0.24=24,
故实体店和网店至少有一边销售量不低于50的天数为66+38-24=80.
(2)由题意,设该实体店一天售出x件,则获利为(50x-1 700)元,50x-1 700≥800 x≥50.
设该实体店一天获利不低于800元为事件A,则P(A)=P(x≥50)=(0.032+0.020+0.012+0.012)×5=0.38.
故该实体店一天获利不低于800元的概率为0.38.
独立性检验
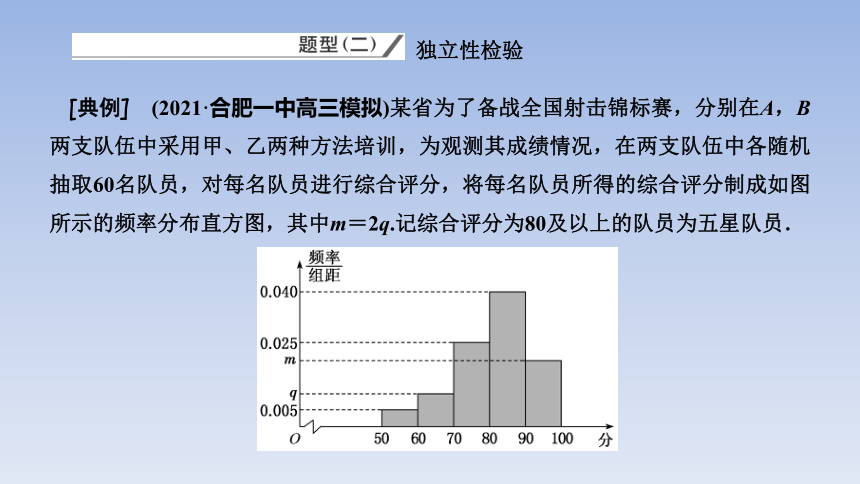
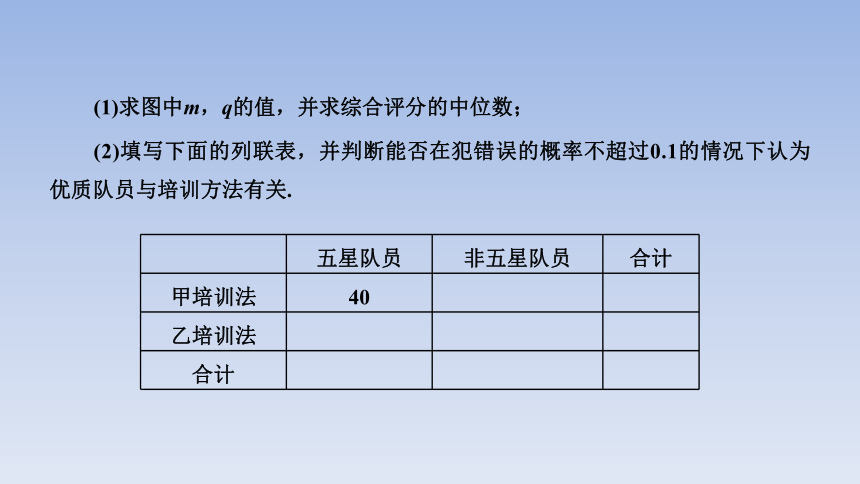
[典例] (2021·合肥一中高三模拟)某省为了备战全国射击锦标赛,分别在A,B两支队伍中采用甲、乙两种方法培训,为观测其成绩情况,在两支队伍中各随机抽取60名队员,对每名队员进行综合评分,将每名队员所得的综合评分制成如图所示的频率分布直方图,其中m=2q.记综合评分为80及以上的队员为五星队员.
五星队员 非五星队员 合计
甲培训法 40
乙培训法
合计
(1)求图中m,q的值,并求综合评分的中位数;
(2)填写下面的列联表,并判断能否在犯错误的概率不超过0.1的情况下认为优质队员与培训方法有关.
[对点训练]
(2021·新乡三模)青少年近视问题已经成为影响青少年健康的一个重要问题,习近平总书记连续作出重要指示,要求“全社会都要行动起来,共同呵护好孩子的眼睛,让他们拥有一个光明的未来”.某机构为了解使用电子产品对青少年视力的影响,随机抽取了200名青少年,调查他们每天使用电子产品的时间(单位:分钟),根据调查数据按(0,30],(30,60],(60,90],(90,120],(120,150],(150,180]分成6组,得到频数分布表如下:
时间/分 (0,30] (30,60] (60,90] (90,120] (120,150] (150,180]
频数 12 38 72 46 22 10
线性回归分析
[典例] 2020年全面建成小康社会取得伟大历史成就,决战脱贫攻坚取得决定性胜利.某市积极探索区域特色经济,引导商家利用多媒体的优势,对本地特产进行广告宣传,取得了社会效益和经济效益的双丰收,某商家统计了7个月的月广告投入x(单位:万元)与月销量y(单位:万件)的数据如表所示:
(1)已知可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并求y关于x的经验回归方程;
(2)根据(1)的结论,预计月广告投入大于多少万元时,月销量能突破70万件.
月广告投入x/万元 1 2 3 4 5 6 7
月销量y/万件 28 32 35 45 49 52 60
[提分技巧] 求解经验回归方程的3步骤
(2)以频率估计概率,设甲款健身器材使用年限为X(单位:年),则其分布列为
E(X)=5×0.1+6×0.4+7×0.3+8×0.2=6.6;
设乙款健身器材使用年限为Y(单位:年),则其分布列为
E(Y)=5×0.3+6×0.4+7×0.2+8×0.1=6.1.
因为E(X)>E(Y),所以该机构购买甲款健身器材使用更长久.
X 5 6 7 8
P 0.1 0.4 0.3 0.2
Y 5 6 7 8
P 0.3 0.4 0.2 0.1
非线性回归分析
[典例] (2022届·重庆质检)近几年,快递业的迅速发展导致行业内竞争日趋激烈.某快递网点需了解一天中收发一件快递的平均成本y(单位:元)与当天揽收的快递件数x(单位:千件)之间的关系,对该网点近5天的每日揽件量xi(单位:千件)与当日收发一件快递的平均成本yi(单位:元)(i=1,2,3,4,5)数据进行了初步处理,得到下面的散点图及一些统计量的值.
(2)各快递公司为提高快递揽收量并实现总利润的增长,除了提升服务质量、提高时效保障外,价格优惠也是重要策略之一.已知该网点每天揽收快递的件数x(单位:千件)与单件快递的平均价格t(单位:元)之间的关系是x=25—2t(5≤t≤12),收发一件快递的利润等于单件的平均价格减去平均成本,根据(1)中建立的回归方程解决以下问题:
①预测该网点某天揽收2 000件快递可获得的总利润;
②单件快递的平均价格t为何值时,该网点一天内收发快递所获利润的预报值最大?
[提分技巧]
求非线性回归方程的步骤
(1)确定变量,作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)变量置换,通过变量置换把非线性回归问题转化为线性回归问题,并求出线性回归方程;
(4)分析拟合效果:通过计算相关指数或画残差图来判断拟合效果;
(5)根据相应的变换,写出非线性回归方程.
[对点训练]
已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数y(个)和温度x(℃)的7组观测数据,其散点图如图所示:
根据散点图,结合函数知识,可以发现产卵数y和温度x可用方程y=ebx+a来拟合,令z=ln y,结合样本数据可知z与温度x可用线性回归方程来拟合.
根据收集到的数据,计算得到如下值:
大题专攻(一) 统计、统计案例
用样本估计总体
[典例] (2021·全国乙卷)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
[提分技巧]
利用样本的数字特征解决优化决策问题的依据
(1)平均数反映了数据取值的平均水平;标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大,越不稳定;标准差、方差越小,数据的离散程度越小,越稳定.
(2)用样本估计总体就是利用样本的数字特征来描述总体的数字特征.
[对点训练]
某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50的概率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1 200元,每售出一件利润为50元,求该实体店一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量的中位数的估计值(精确到0.01).
解:(1)由题意知,网店销售量不低于50共有(0.068+0.046+0.010+0.008)×5×100=66(天),实体店销售量不低于50共有(0.032+0.020+0.012×2)×5×100=38(天),实体店和网店销售量都不低于50的天数为100×0.24=24,
故实体店和网店至少有一边销售量不低于50的天数为66+38-24=80.
(2)由题意,设该实体店一天售出x件,则获利为(50x-1 700)元,50x-1 700≥800 x≥50.
设该实体店一天获利不低于800元为事件A,则P(A)=P(x≥50)=(0.032+0.020+0.012+0.012)×5=0.38.
故该实体店一天获利不低于800元的概率为0.38.
独立性检验
[典例] (2021·合肥一中高三模拟)某省为了备战全国射击锦标赛,分别在A,B两支队伍中采用甲、乙两种方法培训,为观测其成绩情况,在两支队伍中各随机抽取60名队员,对每名队员进行综合评分,将每名队员所得的综合评分制成如图所示的频率分布直方图,其中m=2q.记综合评分为80及以上的队员为五星队员.
五星队员 非五星队员 合计
甲培训法 40
乙培训法
合计
(1)求图中m,q的值,并求综合评分的中位数;
(2)填写下面的列联表,并判断能否在犯错误的概率不超过0.1的情况下认为优质队员与培训方法有关.
[对点训练]
(2021·新乡三模)青少年近视问题已经成为影响青少年健康的一个重要问题,习近平总书记连续作出重要指示,要求“全社会都要行动起来,共同呵护好孩子的眼睛,让他们拥有一个光明的未来”.某机构为了解使用电子产品对青少年视力的影响,随机抽取了200名青少年,调查他们每天使用电子产品的时间(单位:分钟),根据调查数据按(0,30],(30,60],(60,90],(90,120],(120,150],(150,180]分成6组,得到频数分布表如下:
时间/分 (0,30] (30,60] (60,90] (90,120] (120,150] (150,180]
频数 12 38 72 46 22 10
线性回归分析
[典例] 2020年全面建成小康社会取得伟大历史成就,决战脱贫攻坚取得决定性胜利.某市积极探索区域特色经济,引导商家利用多媒体的优势,对本地特产进行广告宣传,取得了社会效益和经济效益的双丰收,某商家统计了7个月的月广告投入x(单位:万元)与月销量y(单位:万件)的数据如表所示:
(1)已知可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并求y关于x的经验回归方程;
(2)根据(1)的结论,预计月广告投入大于多少万元时,月销量能突破70万件.
月广告投入x/万元 1 2 3 4 5 6 7
月销量y/万件 28 32 35 45 49 52 60
[提分技巧] 求解经验回归方程的3步骤
(2)以频率估计概率,设甲款健身器材使用年限为X(单位:年),则其分布列为
E(X)=5×0.1+6×0.4+7×0.3+8×0.2=6.6;
设乙款健身器材使用年限为Y(单位:年),则其分布列为
E(Y)=5×0.3+6×0.4+7×0.2+8×0.1=6.1.
因为E(X)>E(Y),所以该机构购买甲款健身器材使用更长久.
X 5 6 7 8
P 0.1 0.4 0.3 0.2
Y 5 6 7 8
P 0.3 0.4 0.2 0.1
非线性回归分析
[典例] (2022届·重庆质检)近几年,快递业的迅速发展导致行业内竞争日趋激烈.某快递网点需了解一天中收发一件快递的平均成本y(单位:元)与当天揽收的快递件数x(单位:千件)之间的关系,对该网点近5天的每日揽件量xi(单位:千件)与当日收发一件快递的平均成本yi(单位:元)(i=1,2,3,4,5)数据进行了初步处理,得到下面的散点图及一些统计量的值.
(2)各快递公司为提高快递揽收量并实现总利润的增长,除了提升服务质量、提高时效保障外,价格优惠也是重要策略之一.已知该网点每天揽收快递的件数x(单位:千件)与单件快递的平均价格t(单位:元)之间的关系是x=25—2t(5≤t≤12),收发一件快递的利润等于单件的平均价格减去平均成本,根据(1)中建立的回归方程解决以下问题:
①预测该网点某天揽收2 000件快递可获得的总利润;
②单件快递的平均价格t为何值时,该网点一天内收发快递所获利润的预报值最大?
[提分技巧]
求非线性回归方程的步骤
(1)确定变量,作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)变量置换,通过变量置换把非线性回归问题转化为线性回归问题,并求出线性回归方程;
(4)分析拟合效果:通过计算相关指数或画残差图来判断拟合效果;
(5)根据相应的变换,写出非线性回归方程.
[对点训练]
已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数y(个)和温度x(℃)的7组观测数据,其散点图如图所示:
根据散点图,结合函数知识,可以发现产卵数y和温度x可用方程y=ebx+a来拟合,令z=ln y,结合样本数据可知z与温度x可用线性回归方程来拟合.
根据收集到的数据,计算得到如下值:
同课章节目录
