大题专攻(一) “立体几何”中的空间角与距离问题 课件(共23张PPT)
文档属性
| 名称 | 大题专攻(一) “立体几何”中的空间角与距离问题 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:10:55 | ||
图片预览







文档简介
(共23张PPT)
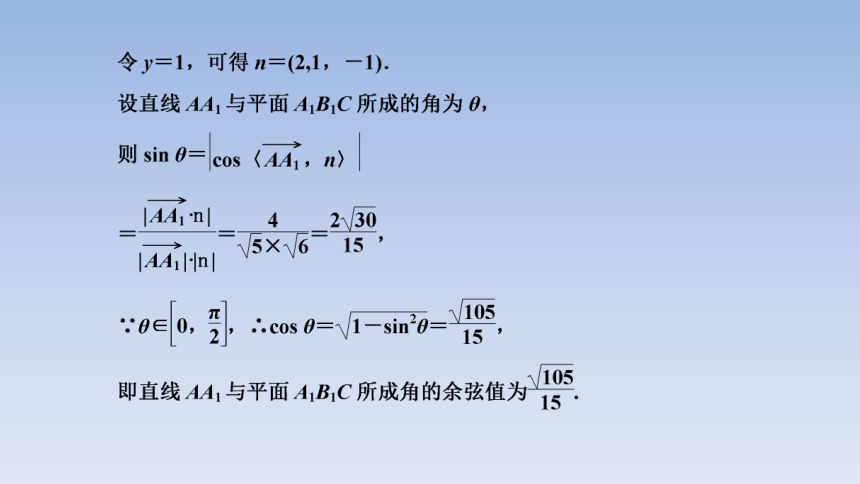
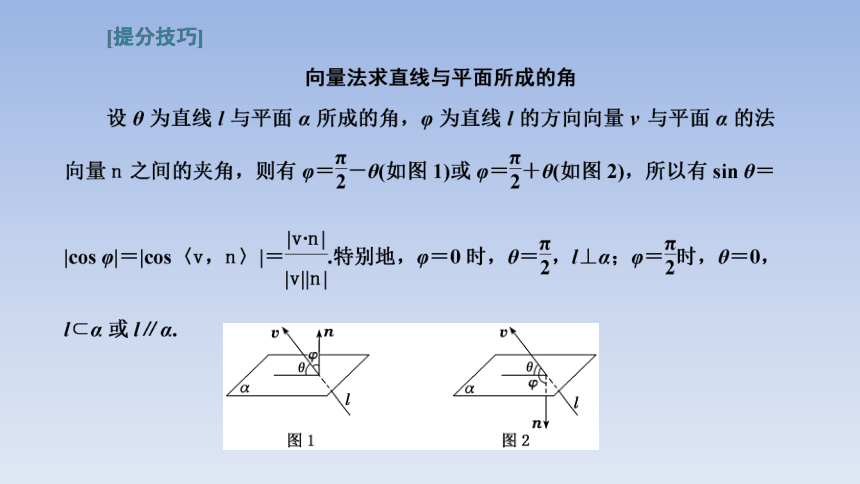
[解题微“点”]
切入点 (1)在平面ACM内找与PB平行的线;
(2)建立坐标系,利用向量法求解
迁移点 (1)把线面平行问题转化为线线平行问题;
(2)把求两平面夹角问题转化为求两法向量的夹角问题
障碍点 不会建系.本题不能直接建系,需根据侧面PAB⊥底面ABCD,作交线AB的垂线,可得平面ABCD的垂线,从而建立坐标系
[对点训练]
(2021·滨州一模)如图1所示,在平行六面体ABCD A1B1C1D1中,底面ABCD是边长为4的正方形.过点A的平面与棱BB1,CC1,DD1分别相交于E,F,G三点,且CF=3,DG=2.
(1)求BE的长;
(2)若平行六面体ABCD A1B1C1D1是侧棱长为6的直四棱柱(如图2),求平面ABCD与平面AED1所成锐二面角的余弦值.
解:(1)如图,过点G作GH平行于DC,与棱CC1相交于点H,则四边形GHCD为平行四边形,所以CH=2,GH=DC,GH∥DC,
又AB=DC,AB∥DC,所以GH=AB,GH∥AB,
则四边形ABHG为平行四边形,所以AG∥BH.
又因为平面BCC1B1∥平面ADD1A1,平面AEFG∩平面BCC1B1=EF,平面AEFG∩平面ADD1A1=AG,所以AG∥EF,所以BH∥EF,又BE∥HF,所以四边形BEFH为平行四边形,则BE=HF=1.
[解题微“点”]
切入点 (1)在平面ACM内找与PB平行的线;
(2)建立坐标系,利用向量法求解
迁移点 (1)把线面平行问题转化为线线平行问题;
(2)把求两平面夹角问题转化为求两法向量的夹角问题
障碍点 不会建系.本题不能直接建系,需根据侧面PAB⊥底面ABCD,作交线AB的垂线,可得平面ABCD的垂线,从而建立坐标系
[对点训练]
(2021·滨州一模)如图1所示,在平行六面体ABCD A1B1C1D1中,底面ABCD是边长为4的正方形.过点A的平面与棱BB1,CC1,DD1分别相交于E,F,G三点,且CF=3,DG=2.
(1)求BE的长;
(2)若平行六面体ABCD A1B1C1D1是侧棱长为6的直四棱柱(如图2),求平面ABCD与平面AED1所成锐二面角的余弦值.
解:(1)如图,过点G作GH平行于DC,与棱CC1相交于点H,则四边形GHCD为平行四边形,所以CH=2,GH=DC,GH∥DC,
又AB=DC,AB∥DC,所以GH=AB,GH∥AB,
则四边形ABHG为平行四边形,所以AG∥BH.
又因为平面BCC1B1∥平面ADD1A1,平面AEFG∩平面BCC1B1=EF,平面AEFG∩平面ADD1A1=AG,所以AG∥EF,所以BH∥EF,又BE∥HF,所以四边形BEFH为平行四边形,则BE=HF=1.
同课章节目录
