小题考法 概率与统计 课件(共50张PPT)
文档属性
| 名称 | 小题考法 概率与统计 课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:16:07 | ||
图片预览











文档简介
(共50张PPT)
第四板块 概率与统计
明明白白知高考
概率与统计、统计案例是高考的重点内容,从近两年高考来看,本板块内容在难度上略有下降,但在创新上继续保持.
1.从题型题量上看:题型以选择、填空、解答为主,二年四卷均以“2小1大”的形式出现,总分约22分,解答题综合性难度上略有增加.如2021年Ⅱ卷中出现与导数结合的问题.
2.从考查内容上看:本板块内容在选择题、填空题中主要考查抽样方法、古典概型、用样本估计总体、正态分布等,此板块易设置多选题,要注意对多选题的训练;解答题常利用排列、组合以及生产、生活真实情境为背景考查离散型随机变量的分布列、期望、方差、二项分布和正态分布、统计案例等问题,注重阅读理解与处理信息能力的考查.
融会贯通串知识
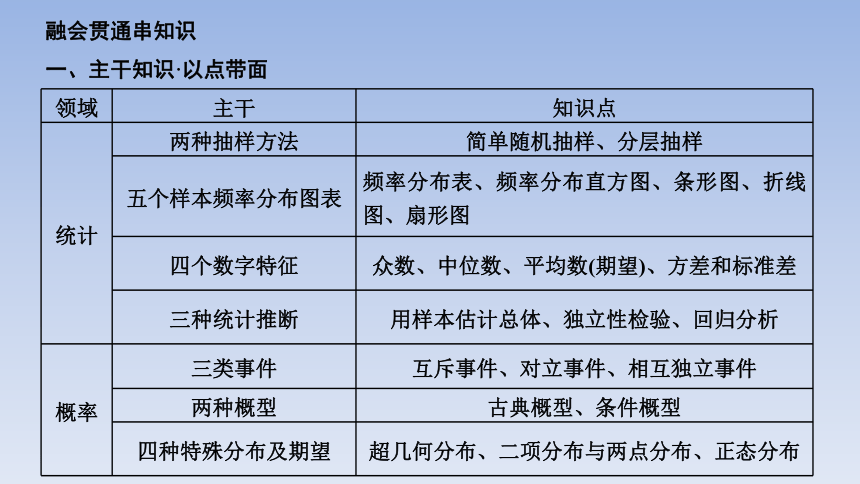
一、主干知识·以点带面
领域 主干 知识点
统计 两种抽样方法 简单随机抽样、分层抽样
五个样本频率分布图表 频率分布表、频率分布直方图、条形图、折线图、扇形图
四个数字特征 众数、中位数、平均数(期望)、方差和标准差
三种统计推断 用样本估计总体、独立性检验、回归分析
概率 三类事件 互斥事件、对立事件、相互独立事件
两种概型 古典概型、条件概型
四种特殊分布及期望 超几何分布、二项分布与两点分布、正态分布
2.概念理解不到位
(1)互斥事件与对立事件关系模糊;
(2)对样本的数字特征认识不到位;
(3)条件概率与二项分布问题理解有误.
3.求离散型随机变量的分布列时忽视所有事件的概率和为1.
2.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
解析:由频率分布直方图可知,该地农户家庭年收入低于4.5万元的农户比率约为0.02+0.04=0.06,所以A正确;该地农户家庭年收入不低于10.5万元的农户比率约为0.02+0.02+0.02+0.04=0.10,所以B正确;由频率分布直方图可知,该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.1+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5,所以C不正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比率约为0.1+0.14+0.2+0.2=0.64>0.5,所以D正确.故选C.
答案:C
4.(多选)某人退休前后各类支出情况如下,已知退休前工资收入为8 000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1 500元,则下面结论中正确的是 ( )
A.该教师退休前每月储蓄支出2 400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休后工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
解析:∵退休前工资收入为8 000元/月,每月储蓄的金额占30%,则该教师退休前每月储蓄支出8 000×30%=2 400元,故A正确;
该教师退休后每月储蓄的金额比退休前每月储蓄的金额少1 500元,
则该教师退休后每月储蓄的金额为900元,设该教师退休工资收入为x元/月,则x·15%=900,即x=6 000元/月,故C正确;
该教师退休前的旅行支出为8 000×5%=400元,退休后的旅行支出为6 000×15%=900元,
∴该教师退休后的旅行支出是退休前旅行支出的2.25倍,故B错误;
该教师退休前的其他支出为8 000×20%=1 600元,退休后的其他支出为6 000×25%=1 500元,
∴该教师退休后的其他支出比退休前的其他支出少,故D正确.
答案:ACD
[提分技巧]
1.数字特征的意义
平均数与方差都是重要的数字特征,是对数据的一种简明描述,它们所反映的情况有着重要的实际意义.平均数、中位数、众数描述数据的集中趋势,方差和标准差描述数据的波动大小.
2.频率分布直方图中常见问题及解题策略
(1)已知频率分布直方图中的部分数据求其他数据.可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1就可以求出其他数据.
(2)已知频率分布直方图,求某个范围内的数据.可利用图形及某范围结合求解.
[解题微“点”]
切入点 分类讨论所求概率的事件所包含的样本点数,即分为“甲同学选马”与“甲同学选牛”两种情况
隐藏点 当甲同学选马时,乙同学只有两种选择
[提分技巧]
(1)解决古典概型问题的关键是求基本事件个数,其常用方法有:枚举法、树状图法,利用排列组合知识计算.
(2)对于较复杂的事件所包含的基本事件个数的计算,要利用分类讨论思想、正难则反的思想方法求解.
2.(2021·宝鸡一模)某“防震减灾科普示范学校”组织4名男生、6名女生志愿者到社区进行防震减灾图片宣讲,若这些选派学生只考虑性别,则派往甲社区宣讲的3人中至少有2名男生的概率为________.
相互独立事件的概率与条件概率
[讲评提能]
[典例] (1)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75
C.0.6 D.0.45
(2)(2021·新高考Ⅰ卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则 ( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
[答案] (1)A (2)B
[提分技巧]
1.求独立事件概率的关键点
(1)紧扣定义,正确判断相互独立事件;
(2)能分解独立事件为几个互斥事件的和;
(3)能正确运用公式P(AB)=P(A)P(B).
2.条件概率的求法
答案:ACD
[过关训练]
1.某市为弘扬我国优秀的传统文化,组织全市10万中小学生参加网络古诗词知识答题比赛,总分100分,经过分析比赛成绩,发现成绩X服从正态分布N(82,16),请估计比赛成绩不小于90分的学生人数约为 ( )
参考数据:P(μ-σA.2 300 B.3 170
C.3 415 D.460
答案: A
3.一个袋中有大小、形状相同的小球,其中红球1个、黑球2个,现随机等可能取出小球,当有放回依次取出两个小球时,记取出的红球数为ξ1;当无放回依次取出两个小球时,记取出的红球数为ξ2,则 ( )
A.E(ξ1)B.E(ξ1)=E(ξ2),D(ξ1)>D(ξ2)
C.E(ξ1)=E(ξ2),D(ξ1)D.E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
解析:ξ1的可能取值为0,1,2,ξ1~B,E(ξ1)=2×=,D(ξ1)=2××=;ξ2的可能取值为0,1,P(ξ2=0)=×=,P(ξ2=1)=×+×=,∴E(ξ2)=0×+1×=,D(ξ2)=2×+2×=.
∴E(ξ1)=E(ξ2),D(ξ1)>D(ξ2).故选B.
答案:B
1.(与生产、生活相结合)(多选)某生活超市2020年第四季度各区域营业收入占比和净利润占比如下表所示:
该生活超市本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),则 ( )
A.本季度此生活超市营业收入最低的是熟食区
B.本季度此生活超市的营业净利润超过一半来自生鲜区
C.本季度此生活超市营业利润最高的是日用品区
D.本季度此生活超市生鲜区的营业利润率超过50%
生鲜区 熟食区 乳制品区 日用品区 其他类
营业收入占比 48.6% 15.8% 20.1% 10.8% 4.7%
净利润占比 65.8% -4.3% 16.5% 20.2% 1.8%
2.(体现数学应用)(多选)5G技术的运营不仅仅提高了传输速度,更拓宽了网络资源的服务范围,目前,我国加速了5G技术的融合与创新,前景美好!某手机商场统计了5个月的5G手机销量,如下表所示:
月份 2020年6月 2020年7月 2020年8月 2020年9月 2020年10月
月份编号x 1 2 3 4 5
销量y/部 52 95 a 185 227
4.(体现数学应用)夏、秋两季,生活在长江口外浅海域的中华鱼洄游到长江,历经三千多公里的溯流搏击,回到金沙江一带产卵繁殖,产后待幼鱼长到15厘米左右,又携带它们旅居外海.一个环保组织曾在金沙江中放生一批中华鱼鱼苗,该批鱼苗中的雌性个体能长成熟的概率为0.15,雌性个体长成熟又能成功溯流产卵繁殖的概率为0.05,若该批鱼苗中的一个雌性个体在长江口外浅海域已长成熟,则其能成功溯流产卵繁殖的概率为________.
第四板块 概率与统计
明明白白知高考
概率与统计、统计案例是高考的重点内容,从近两年高考来看,本板块内容在难度上略有下降,但在创新上继续保持.
1.从题型题量上看:题型以选择、填空、解答为主,二年四卷均以“2小1大”的形式出现,总分约22分,解答题综合性难度上略有增加.如2021年Ⅱ卷中出现与导数结合的问题.
2.从考查内容上看:本板块内容在选择题、填空题中主要考查抽样方法、古典概型、用样本估计总体、正态分布等,此板块易设置多选题,要注意对多选题的训练;解答题常利用排列、组合以及生产、生活真实情境为背景考查离散型随机变量的分布列、期望、方差、二项分布和正态分布、统计案例等问题,注重阅读理解与处理信息能力的考查.
融会贯通串知识
一、主干知识·以点带面
领域 主干 知识点
统计 两种抽样方法 简单随机抽样、分层抽样
五个样本频率分布图表 频率分布表、频率分布直方图、条形图、折线图、扇形图
四个数字特征 众数、中位数、平均数(期望)、方差和标准差
三种统计推断 用样本估计总体、独立性检验、回归分析
概率 三类事件 互斥事件、对立事件、相互独立事件
两种概型 古典概型、条件概型
四种特殊分布及期望 超几何分布、二项分布与两点分布、正态分布
2.概念理解不到位
(1)互斥事件与对立事件关系模糊;
(2)对样本的数字特征认识不到位;
(3)条件概率与二项分布问题理解有误.
3.求离散型随机变量的分布列时忽视所有事件的概率和为1.
2.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
解析:由频率分布直方图可知,该地农户家庭年收入低于4.5万元的农户比率约为0.02+0.04=0.06,所以A正确;该地农户家庭年收入不低于10.5万元的农户比率约为0.02+0.02+0.02+0.04=0.10,所以B正确;由频率分布直方图可知,该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.1+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5,所以C不正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比率约为0.1+0.14+0.2+0.2=0.64>0.5,所以D正确.故选C.
答案:C
4.(多选)某人退休前后各类支出情况如下,已知退休前工资收入为8 000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1 500元,则下面结论中正确的是 ( )
A.该教师退休前每月储蓄支出2 400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休后工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
解析:∵退休前工资收入为8 000元/月,每月储蓄的金额占30%,则该教师退休前每月储蓄支出8 000×30%=2 400元,故A正确;
该教师退休后每月储蓄的金额比退休前每月储蓄的金额少1 500元,
则该教师退休后每月储蓄的金额为900元,设该教师退休工资收入为x元/月,则x·15%=900,即x=6 000元/月,故C正确;
该教师退休前的旅行支出为8 000×5%=400元,退休后的旅行支出为6 000×15%=900元,
∴该教师退休后的旅行支出是退休前旅行支出的2.25倍,故B错误;
该教师退休前的其他支出为8 000×20%=1 600元,退休后的其他支出为6 000×25%=1 500元,
∴该教师退休后的其他支出比退休前的其他支出少,故D正确.
答案:ACD
[提分技巧]
1.数字特征的意义
平均数与方差都是重要的数字特征,是对数据的一种简明描述,它们所反映的情况有着重要的实际意义.平均数、中位数、众数描述数据的集中趋势,方差和标准差描述数据的波动大小.
2.频率分布直方图中常见问题及解题策略
(1)已知频率分布直方图中的部分数据求其他数据.可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1就可以求出其他数据.
(2)已知频率分布直方图,求某个范围内的数据.可利用图形及某范围结合求解.
[解题微“点”]
切入点 分类讨论所求概率的事件所包含的样本点数,即分为“甲同学选马”与“甲同学选牛”两种情况
隐藏点 当甲同学选马时,乙同学只有两种选择
[提分技巧]
(1)解决古典概型问题的关键是求基本事件个数,其常用方法有:枚举法、树状图法,利用排列组合知识计算.
(2)对于较复杂的事件所包含的基本事件个数的计算,要利用分类讨论思想、正难则反的思想方法求解.
2.(2021·宝鸡一模)某“防震减灾科普示范学校”组织4名男生、6名女生志愿者到社区进行防震减灾图片宣讲,若这些选派学生只考虑性别,则派往甲社区宣讲的3人中至少有2名男生的概率为________.
相互独立事件的概率与条件概率
[讲评提能]
[典例] (1)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75
C.0.6 D.0.45
(2)(2021·新高考Ⅰ卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则 ( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
[答案] (1)A (2)B
[提分技巧]
1.求独立事件概率的关键点
(1)紧扣定义,正确判断相互独立事件;
(2)能分解独立事件为几个互斥事件的和;
(3)能正确运用公式P(AB)=P(A)P(B).
2.条件概率的求法
答案:ACD
[过关训练]
1.某市为弘扬我国优秀的传统文化,组织全市10万中小学生参加网络古诗词知识答题比赛,总分100分,经过分析比赛成绩,发现成绩X服从正态分布N(82,16),请估计比赛成绩不小于90分的学生人数约为 ( )
参考数据:P(μ-σ
C.3 415 D.460
答案: A
3.一个袋中有大小、形状相同的小球,其中红球1个、黑球2个,现随机等可能取出小球,当有放回依次取出两个小球时,记取出的红球数为ξ1;当无放回依次取出两个小球时,记取出的红球数为ξ2,则 ( )
A.E(ξ1)
C.E(ξ1)=E(ξ2),D(ξ1)
解析:ξ1的可能取值为0,1,2,ξ1~B,E(ξ1)=2×=,D(ξ1)=2××=;ξ2的可能取值为0,1,P(ξ2=0)=×=,P(ξ2=1)=×+×=,∴E(ξ2)=0×+1×=,D(ξ2)=2×+2×=.
∴E(ξ1)=E(ξ2),D(ξ1)>D(ξ2).故选B.
答案:B
1.(与生产、生活相结合)(多选)某生活超市2020年第四季度各区域营业收入占比和净利润占比如下表所示:
该生活超市本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),则 ( )
A.本季度此生活超市营业收入最低的是熟食区
B.本季度此生活超市的营业净利润超过一半来自生鲜区
C.本季度此生活超市营业利润最高的是日用品区
D.本季度此生活超市生鲜区的营业利润率超过50%
生鲜区 熟食区 乳制品区 日用品区 其他类
营业收入占比 48.6% 15.8% 20.1% 10.8% 4.7%
净利润占比 65.8% -4.3% 16.5% 20.2% 1.8%
2.(体现数学应用)(多选)5G技术的运营不仅仅提高了传输速度,更拓宽了网络资源的服务范围,目前,我国加速了5G技术的融合与创新,前景美好!某手机商场统计了5个月的5G手机销量,如下表所示:
月份 2020年6月 2020年7月 2020年8月 2020年9月 2020年10月
月份编号x 1 2 3 4 5
销量y/部 52 95 a 185 227
4.(体现数学应用)夏、秋两季,生活在长江口外浅海域的中华鱼洄游到长江,历经三千多公里的溯流搏击,回到金沙江一带产卵繁殖,产后待幼鱼长到15厘米左右,又携带它们旅居外海.一个环保组织曾在金沙江中放生一批中华鱼鱼苗,该批鱼苗中的雌性个体能长成熟的概率为0.15,雌性个体长成熟又能成功溯流产卵繁殖的概率为0.05,若该批鱼苗中的一个雌性个体在长江口外浅海域已长成熟,则其能成功溯流产卵繁殖的概率为________.
同课章节目录
