小题考法(二) 基本初等函数、函数的应用 课件(共39张PPT)
文档属性
| 名称 | 小题考法(二) 基本初等函数、函数的应用 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 11:17:10 | ||
图片预览











文档简介
(共39张PPT)
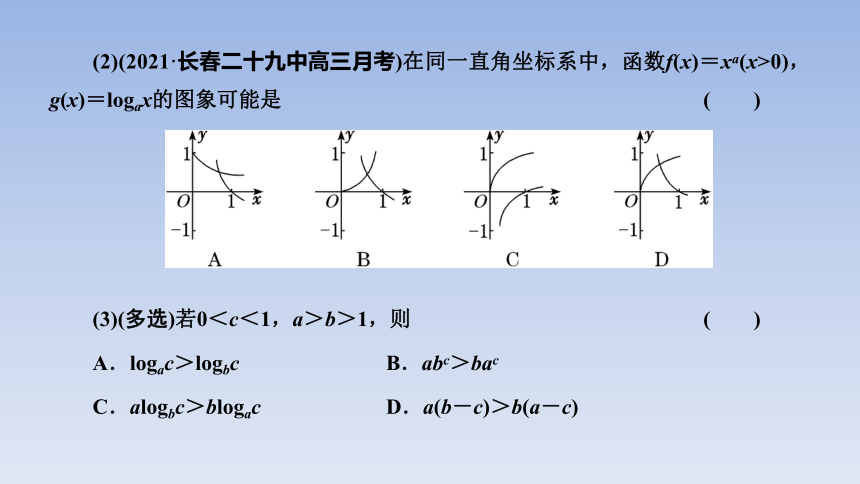
(2)(2021·长春二十九中高三月考)在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是 ( )
(3)(多选)若0<c<1,a>b>1,则 ( )
A.logac>logbc B.abc>bac
C.alogbc>blogac D.a(b-c)>b(a-c)
对于C,由A知logbc<logac<0,又a>b>1,所以alogbc<blogbc,blogbc<blogac,所以alogbc<blogac,故C不正确;
对于D,因为0<c<1,a>b>1,所以ac>bc,所以-ac<-bc,所以ab-ac<ab-bc,即a(b-c)<b(a-c),故D不正确.综上所述,选A、B.
[答案] (1)AC (2)D (3)AB
[提分技巧]
(1)指数函数、对数函数的图象和性质受底数a的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a的范围.
(2)研究对数函数的性质,应注意真数与底数的限制条件.如求f(x)=ln(x2-3x+2)的单调区间时,容易只考虑t=x2-3x+2与函数y=ln t的单调性,忽视t>0的限制条件.
[过关训练]
1.(2021·济宁一模)已知a=sin 2,b=log20.2,c=20.2,则 ( )
A.a>b>c B.c>a>b
C.b>a>c D.c>b>a
[提分技巧]
解决函数模型的实际应用问题时,首先要耐心、细心地审清题意,弄清各量之间的关系,再建立函数关系式,然后借助函数的知识求解,解答后再回到实际问题中去.
[过关训练]
1.(2021·大理模拟)“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,且该果蔬所需物流时间为3天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过 ( )
A.9 ℃ B.12 ℃
C.18 ℃ D.20 ℃
2.(2021·重庆八中适应性考试)某市政府加强数学科学研究,计划逐年加大研发资金投入.已知该市政府1980年全年投入研发资金100万元,2020年全年投入研发资金500万元,若每年投入的研发资金的增长率相同,则该市政府2021年全年投入的研发资金约为(本题可用自然对数的近似公式:0<x<0.1时,ln(1+x)≈x.参考数据:ln 5≈1.61,1.140≈45) ( )
A.515 万元 B.520 万元
C.525 万元 D.530 万元
[典例2] (2021·赣州二模)已知定义在R上的函数y=f(x),对任意x都满足f(x+2)=f(x),且当-1≤x≤1时,f(x)=2x2,则函数g(x)=f(x)-ln|x|的零点个数为( )
A.12 B.14
C.15 D.16
[解题微“点”]
切入点 令g(x)=0,即f(x)=ln|x|,问题转化为函数y=f(x)的图象与函数y=ln|x|图象的交点个数问题
障碍点 利用函数值的大小判断函数y=ln|x|与y=f(x)是否有交点,准确作出y=f(x)与y=ln|x|的大致图象即可
[解题微“点”]
切入点 把函数y=f(x)-k(x-1)的零点个数为5,转化为函数y=f(x)与y=k(x-1)的图象交点个数为5,根据图象求k的取值范围
关键点 由f(x)是偶函数,则f(-x)=f(x),由f(x-1)是奇函数,得f(x-1)=-f(-x-1),即f(x)=-f(-x-2),则f(-x)=-f(-x-2),f(x)=-f(x-2),可得f(x)的周期为4,从而作出f(x)的图象
[提分技巧]
1.判断函数零点个数或存在范围的主要方法
(1)解方程f(x)=0,直接求零点;
(2)利用零点存在定理;
(3)数形结合法:对于给定的函数不能直接求解或画出图形,常会通过分解转化为两个能画出的函数图象交点问题.
2.解决由函数零点的存在情况求参数的值或取值范围问题,关键是利用函数方程思想或数形结合思想,构建关于参数的方程或不等式求解.
解析:各次操作后的数据如下表:
4.(强化数学建模)某同学设想用“高个子系数k”来刻画成年男子的高个子的程度,他认为,成年男子身高160 cm及以下不算高个子,其高个子系数k应为0;身高190 cm及以上的是理所当然的高个子,其高个子系数k应为1.依据该同学想法可得到的合理的成年男子高个子系数k关于身高x(单位:cm)的函数关系式为________.
(2)(2021·长春二十九中高三月考)在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是 ( )
(3)(多选)若0<c<1,a>b>1,则 ( )
A.logac>logbc B.abc>bac
C.alogbc>blogac D.a(b-c)>b(a-c)
对于C,由A知logbc<logac<0,又a>b>1,所以alogbc<blogbc,blogbc<blogac,所以alogbc<blogac,故C不正确;
对于D,因为0<c<1,a>b>1,所以ac>bc,所以-ac<-bc,所以ab-ac<ab-bc,即a(b-c)<b(a-c),故D不正确.综上所述,选A、B.
[答案] (1)AC (2)D (3)AB
[提分技巧]
(1)指数函数、对数函数的图象和性质受底数a的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a的范围.
(2)研究对数函数的性质,应注意真数与底数的限制条件.如求f(x)=ln(x2-3x+2)的单调区间时,容易只考虑t=x2-3x+2与函数y=ln t的单调性,忽视t>0的限制条件.
[过关训练]
1.(2021·济宁一模)已知a=sin 2,b=log20.2,c=20.2,则 ( )
A.a>b>c B.c>a>b
C.b>a>c D.c>b>a
[提分技巧]
解决函数模型的实际应用问题时,首先要耐心、细心地审清题意,弄清各量之间的关系,再建立函数关系式,然后借助函数的知识求解,解答后再回到实际问题中去.
[过关训练]
1.(2021·大理模拟)“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=eax+b(a,b为常数),若该果蔬在6 ℃的保鲜时间为216小时,在24 ℃的保鲜时间为8小时,且该果蔬所需物流时间为3天,则物流过程中果蔬的储藏温度(假设物流过程中恒温)最高不能超过 ( )
A.9 ℃ B.12 ℃
C.18 ℃ D.20 ℃
2.(2021·重庆八中适应性考试)某市政府加强数学科学研究,计划逐年加大研发资金投入.已知该市政府1980年全年投入研发资金100万元,2020年全年投入研发资金500万元,若每年投入的研发资金的增长率相同,则该市政府2021年全年投入的研发资金约为(本题可用自然对数的近似公式:0<x<0.1时,ln(1+x)≈x.参考数据:ln 5≈1.61,1.140≈45) ( )
A.515 万元 B.520 万元
C.525 万元 D.530 万元
[典例2] (2021·赣州二模)已知定义在R上的函数y=f(x),对任意x都满足f(x+2)=f(x),且当-1≤x≤1时,f(x)=2x2,则函数g(x)=f(x)-ln|x|的零点个数为( )
A.12 B.14
C.15 D.16
[解题微“点”]
切入点 令g(x)=0,即f(x)=ln|x|,问题转化为函数y=f(x)的图象与函数y=ln|x|图象的交点个数问题
障碍点 利用函数值的大小判断函数y=ln|x|与y=f(x)是否有交点,准确作出y=f(x)与y=ln|x|的大致图象即可
[解题微“点”]
切入点 把函数y=f(x)-k(x-1)的零点个数为5,转化为函数y=f(x)与y=k(x-1)的图象交点个数为5,根据图象求k的取值范围
关键点 由f(x)是偶函数,则f(-x)=f(x),由f(x-1)是奇函数,得f(x-1)=-f(-x-1),即f(x)=-f(-x-2),则f(-x)=-f(-x-2),f(x)=-f(x-2),可得f(x)的周期为4,从而作出f(x)的图象
[提分技巧]
1.判断函数零点个数或存在范围的主要方法
(1)解方程f(x)=0,直接求零点;
(2)利用零点存在定理;
(3)数形结合法:对于给定的函数不能直接求解或画出图形,常会通过分解转化为两个能画出的函数图象交点问题.
2.解决由函数零点的存在情况求参数的值或取值范围问题,关键是利用函数方程思想或数形结合思想,构建关于参数的方程或不等式求解.
解析:各次操作后的数据如下表:
4.(强化数学建模)某同学设想用“高个子系数k”来刻画成年男子的高个子的程度,他认为,成年男子身高160 cm及以下不算高个子,其高个子系数k应为0;身高190 cm及以上的是理所当然的高个子,其高个子系数k应为1.依据该同学想法可得到的合理的成年男子高个子系数k关于身高x(单位:cm)的函数关系式为________.
同课章节目录
