专题一 1.1 集合、常用逻辑用语、推理小题组合练 课件(共29张PPT)
文档属性
| 名称 | 专题一 1.1 集合、常用逻辑用语、推理小题组合练 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 07:02:15 | ||
图片预览







文档简介
(共29张PPT)
1.1 集合、常用逻辑用语、推理小题组合练
第三部分
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.A∪B={x|x∈A或x∈B};A∩B={x|x∈A,且x∈B}; UA={x|x∈U,且x A};A∪B=A B A,A∩B=A A B.
2.含有n个元素的集合,其子集、真子集、非空真子集的个数依次为2n,2n-1,2n-2.
3.若p q,则p是q的充分条件,q是p的必要条件;若p q,则p是q的充要条件.
4.充要条件的三种判断方法:(1)定义法,(2)集合法,(3)等价转化法.
5.“ x∈M,p(x)”的否定为“ x0∈M, p(x0)”;“ x0∈M,p(x0)”的否定为“ x∈M, p(x)”.
考向训练 限时通关
考向一
集合的概念及运算
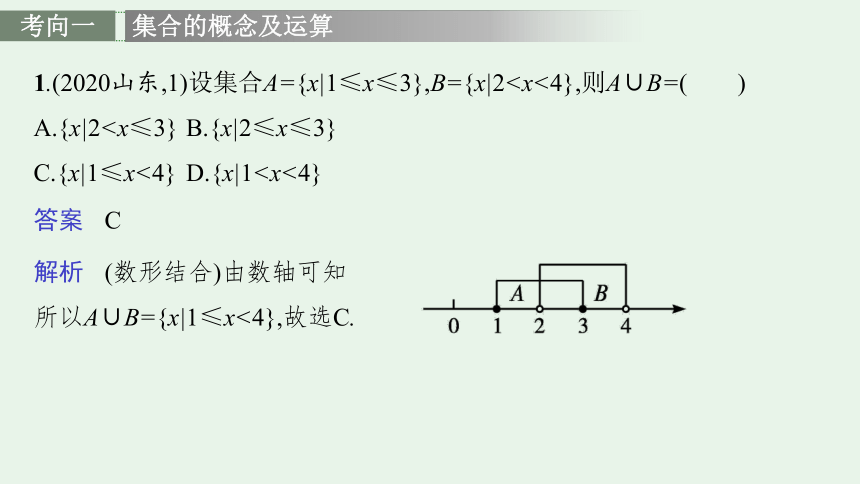
1.(2020山东,1)设集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|1答案 C
解析 (数形结合)由数轴可知
所以A∪B={x|1≤x<4},故选C.
2.(2020全国Ⅲ,理1)已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为( )
A.2 B.3 C.4 D.6
答案 C
解析 满足x,y∈N*,y≥x,且x+y=8的元素(x,y)有(1,7),(2,6),(3,5),(4,4),共4个,故A∩B中元素的个数为4.
3.(2020全国Ⅱ,理1)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则 U(A∪B)=( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
答案 A
解析 ∵A∪B={-1,0,1,2},
∴ U(A∪B)={-2,3}.故选A.
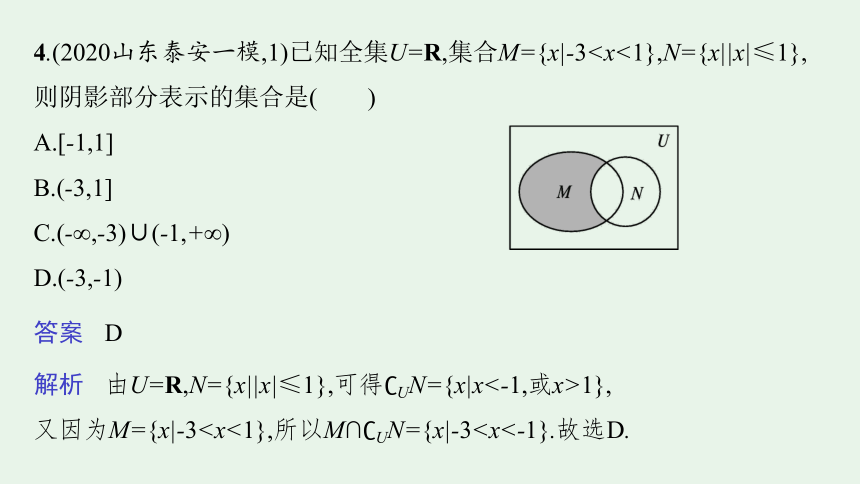
4.(2020山东泰安一模,1)已知全集U=R,集合M={x|-3A.[-1,1]
B.(-3,1]
C.(-∞,-3)∪(-1,+∞)
D.(-3,-1)
答案 D
解析 由U=R,N={x||x|≤1},可得 UN={x|x<-1,或x>1},
又因为M={x|-35.(多选)(2020福建双十中学期中,1)集合A,B是实数集R的子集,定义
A-B={x|x∈A,且x B},若集合A={y|y=(x-1)2+1,0≤x≤3},
B={y|y=x2+1,1≤x≤3},则以下说法正确的是( )
A.A=[-1,5] B.B=[2,10]
C.A-B=[1,2) D.B-A=(5,10]
答案 BCD
解析 A={y|y=(x-1)2+1,0≤x≤3}={y|1≤y≤5},
B={y|y=x2+1,1≤x≤3}={y|2≤y≤10},故A-B={y|y∈A,
且y B}={y|1≤y<2},B-A={y|y∈B,且y A}={y|56.(2020江苏南京六校5月联考,1)已知集合A={x|x2-2x<0},B={x|x<1},则A∪B= .
答案 (-∞,2)
解析 ∵集合A={x|x2-2x<0}={x|0∴A∪B={x|x<2}.
考向二
充分、必要、充要条件
7.(2020浙江,6)已知空间中不过同一点的三条直线l,m,n.“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
答案 B
解析 由条件可知,当m,n,l在同一平面内时,三条直线不一定两两相交,有可能两条直线平行,或三条直线平行;反过来,当空间中不过同一点的三条直线m,n,l两两相交时,如图,三个不同的交点确定一个平面,则m,n,l在同一平面内,所以“m,n,l共面”是“m,n,l两两相交”的必要不充分条件.故选B.
8.(2020北京,9)已知α,β∈R,则“存在k∈Z使得α=kπ+(-1)kβ”是“sin α=sin β”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案 C
解析 当存在k∈Z使得α=kπ+(-1)kβ时,若k为偶数,则sin α=sin(kπ+β)=sin β;
若k为奇数,则sin α=sin(kπ-β)=sin[(k-1)π+π-β]=sin(π-β)=sin β.
当sin α=sin β时,α=β+2mπ或α+β=π+2mπ,m∈Z,即α=kπ+(-1)kβ(k=2m)或α=kπ+(-1)kβ(k=2m+1),
亦即存在k∈Z使得α=kπ+(-1)kβ.
所以“存在k∈Z使得α=kπ+(-1)kβ”是“sin α=sin β”的充要条件.故选C.
9.(2020山东菏泽一模,3)2019年12月,湖北省武汉市发现多起病毒性肺炎病例.2020年1月12日,世界卫生组织正式将造成此次肺炎疫情的病毒命名为“2019新型冠状病毒”.2020年2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为COVID-19(新冠肺炎).新冠肺炎患者早期症状是发热、干咳、浑身乏力等外部表征.“某人表现为发热、干咳、浑身乏力”是“新冠肺炎患者”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 由题意得,表现为发热、干咳、浑身乏力者不一定是感染新型冠状病毒,而新型冠状病毒感染者早期症状表现为发热、干咳、浑身乏力等外部表征.因而“某人表现为发热、干咳、浑身乏力”是“新冠肺炎患者”的必要不充分条件.
10.(2020安徽合肥一中模拟,理2)已知命题p:(a-2)x2+2(a-2)x-2<0(a∈R)的解集为R,命题q:0A.充分条件 B.必要不充分条件 C.充要条件 D.充分不必要条件
答案 B
解析 (a-2)x2+2(a-2)x-2<0(a∈R)的解集为R,
或a=2,解得011.(多选)(2020南京秦淮中学期末)已知命题p: >1,则命题成立的一个必要不充分条件是( )
A.1答案 BD
选项A中“1选项B中“-1选项C中“-2选项D中“-2考向三
全称量词与存在量词
12.(2020山东淄博一模,3)设m∈R,命题“存在m>0,使方程x2+x-m=0有实根”的否定是( )
A.任意m>0,使方程x2+x-m=0无实根
B.任意m≤0,使方程x2+x-m=0有实根
C.存在m>0,使方程x2+x-m=0无实根
D.存在m≤0,使方程x2+x-m=0有实根
答案 A
解析 由特称命题的否定是全称命题,知“存在m>0,使方程x2+x-m=0有实根”的否定是“任意m>0,使方程x2+x-m=0无实根”.故选A.
答案 AB
14.(2020山东青岛5月模拟,13)已知命题“ x0∈R, -mx0+1<0”是假命题,则实数m的取值范围是 .
答案 [-2,2]
解析 因为命题“ x0∈R, -mx0+1<0”是假命题,所以命题“ x∈R,
x2-mx+1≥0”是真命题,所以Δ=m2-4≥0,所以-2≤m≤2.
考向四
逻辑推理判断题
15.(2020山东潍坊二模,3)甲、乙、丙三人中,一人是律师,一个是医生,一人是记者.已知丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是( )
A.甲是律师,乙是医生,丙是记者
B.甲是医生,乙是记者,丙是律师
C.甲是医生,乙是律师,丙是记者
D.甲是记者,乙是医生,丙是律师
答案 C
解析 由甲的年龄和记者不同,记者的年龄比乙小,得到丙是记者,从而排除B和D;由丙的年龄比医生大且比乙小,得到乙不是医生,从而乙是律师,甲是医生.故选C.
16.甲、乙、丙、丁四位同学参加一次数学智力竞赛,决出了第一名到第四名的四个名次.甲说:“我不是第一名”;乙说:“丁是第一名”;丙说:“乙是第一名”;丁说:“我不是第一名”.成绩公布后,发现这四位同学中只有一位说的是正确的.则获得第一名的同学为( )
A.甲 B.乙 C.丙 D.丁
答案 A
解析 当甲获得第一名时,甲、乙、丙说的都是错的,丁说的是对的,符合条件;
当乙获得第一名时,甲、丙、丁说的都是对的,乙说的是错的,不符合条件;
当丙获得第一名时,甲和丁说的都是对的,乙、丙说的是错的,不符合条件;
当丁获得第一名时,甲和乙说的都是对的,丙、丁说的是错的,不符合条件,故选A.
17.(2020安徽马鞍山二模,16)根据疾病防控的需要,某医院要从感染科抽调两名医生随省医疗队赴武汉参加抗疫工作,现有甲、乙、丙、丁、戊五名优秀医生申请作为志愿者参加.为确定最终驰援武汉的人选,医院领导组五位成员先各推荐两名人员,分别为“丁、戊”“丙、戊”“甲、乙”“乙、戊”“甲、丁”.根据最终入选名单发现五位领导中有一人推荐的两人都没有入选,其余四人推荐的人选中各有一人入选.根据以上信息判断,最后随省医疗队参加抗疫的两名医生分别是 .
答案 乙、丁
解析 五位领导中有一人推荐的两人都没有入选,其余四人推荐的人选中各有一人入选.
设“丁、戊”两人都没入选,那么不含丁、戊的人选组合中还剩“甲、乙”,
这与其余四人推荐的人选中各有一人入选矛盾.
设“丙、戊”两人都没入选,那么不含丙、戊的人选组合中还剩“甲、乙”和“甲、丁”,由题意这两个组合中各有一人入选,则为“乙、丁”,这符合题意,故答案为乙、丁.
1.1 集合、常用逻辑用语、推理小题组合练
第三部分
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.A∪B={x|x∈A或x∈B};A∩B={x|x∈A,且x∈B}; UA={x|x∈U,且x A};A∪B=A B A,A∩B=A A B.
2.含有n个元素的集合,其子集、真子集、非空真子集的个数依次为2n,2n-1,2n-2.
3.若p q,则p是q的充分条件,q是p的必要条件;若p q,则p是q的充要条件.
4.充要条件的三种判断方法:(1)定义法,(2)集合法,(3)等价转化法.
5.“ x∈M,p(x)”的否定为“ x0∈M, p(x0)”;“ x0∈M,p(x0)”的否定为“ x∈M, p(x)”.
考向训练 限时通关
考向一
集合的概念及运算
1.(2020山东,1)设集合A={x|1≤x≤3},B={x|2
解析 (数形结合)由数轴可知
所以A∪B={x|1≤x<4},故选C.
2.(2020全国Ⅲ,理1)已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为( )
A.2 B.3 C.4 D.6
答案 C
解析 满足x,y∈N*,y≥x,且x+y=8的元素(x,y)有(1,7),(2,6),(3,5),(4,4),共4个,故A∩B中元素的个数为4.
3.(2020全国Ⅱ,理1)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则 U(A∪B)=( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
答案 A
解析 ∵A∪B={-1,0,1,2},
∴ U(A∪B)={-2,3}.故选A.
4.(2020山东泰安一模,1)已知全集U=R,集合M={x|-3
B.(-3,1]
C.(-∞,-3)∪(-1,+∞)
D.(-3,-1)
答案 D
解析 由U=R,N={x||x|≤1},可得 UN={x|x<-1,或x>1},
又因为M={x|-3
A-B={x|x∈A,且x B},若集合A={y|y=(x-1)2+1,0≤x≤3},
B={y|y=x2+1,1≤x≤3},则以下说法正确的是( )
A.A=[-1,5] B.B=[2,10]
C.A-B=[1,2) D.B-A=(5,10]
答案 BCD
解析 A={y|y=(x-1)2+1,0≤x≤3}={y|1≤y≤5},
B={y|y=x2+1,1≤x≤3}={y|2≤y≤10},故A-B={y|y∈A,
且y B}={y|1≤y<2},B-A={y|y∈B,且y A}={y|5
答案 (-∞,2)
解析 ∵集合A={x|x2-2x<0}={x|0
考向二
充分、必要、充要条件
7.(2020浙江,6)已知空间中不过同一点的三条直线l,m,n.“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
答案 B
解析 由条件可知,当m,n,l在同一平面内时,三条直线不一定两两相交,有可能两条直线平行,或三条直线平行;反过来,当空间中不过同一点的三条直线m,n,l两两相交时,如图,三个不同的交点确定一个平面,则m,n,l在同一平面内,所以“m,n,l共面”是“m,n,l两两相交”的必要不充分条件.故选B.
8.(2020北京,9)已知α,β∈R,则“存在k∈Z使得α=kπ+(-1)kβ”是“sin α=sin β”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案 C
解析 当存在k∈Z使得α=kπ+(-1)kβ时,若k为偶数,则sin α=sin(kπ+β)=sin β;
若k为奇数,则sin α=sin(kπ-β)=sin[(k-1)π+π-β]=sin(π-β)=sin β.
当sin α=sin β时,α=β+2mπ或α+β=π+2mπ,m∈Z,即α=kπ+(-1)kβ(k=2m)或α=kπ+(-1)kβ(k=2m+1),
亦即存在k∈Z使得α=kπ+(-1)kβ.
所以“存在k∈Z使得α=kπ+(-1)kβ”是“sin α=sin β”的充要条件.故选C.
9.(2020山东菏泽一模,3)2019年12月,湖北省武汉市发现多起病毒性肺炎病例.2020年1月12日,世界卫生组织正式将造成此次肺炎疫情的病毒命名为“2019新型冠状病毒”.2020年2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为COVID-19(新冠肺炎).新冠肺炎患者早期症状是发热、干咳、浑身乏力等外部表征.“某人表现为发热、干咳、浑身乏力”是“新冠肺炎患者”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 由题意得,表现为发热、干咳、浑身乏力者不一定是感染新型冠状病毒,而新型冠状病毒感染者早期症状表现为发热、干咳、浑身乏力等外部表征.因而“某人表现为发热、干咳、浑身乏力”是“新冠肺炎患者”的必要不充分条件.
10.(2020安徽合肥一中模拟,理2)已知命题p:(a-2)x2+2(a-2)x-2<0(a∈R)的解集为R,命题q:0
答案 B
解析 (a-2)x2+2(a-2)x-2<0(a∈R)的解集为R,
或a=2,解得0
A.1
选项A中“1
全称量词与存在量词
12.(2020山东淄博一模,3)设m∈R,命题“存在m>0,使方程x2+x-m=0有实根”的否定是( )
A.任意m>0,使方程x2+x-m=0无实根
B.任意m≤0,使方程x2+x-m=0有实根
C.存在m>0,使方程x2+x-m=0无实根
D.存在m≤0,使方程x2+x-m=0有实根
答案 A
解析 由特称命题的否定是全称命题,知“存在m>0,使方程x2+x-m=0有实根”的否定是“任意m>0,使方程x2+x-m=0无实根”.故选A.
答案 AB
14.(2020山东青岛5月模拟,13)已知命题“ x0∈R, -mx0+1<0”是假命题,则实数m的取值范围是 .
答案 [-2,2]
解析 因为命题“ x0∈R, -mx0+1<0”是假命题,所以命题“ x∈R,
x2-mx+1≥0”是真命题,所以Δ=m2-4≥0,所以-2≤m≤2.
考向四
逻辑推理判断题
15.(2020山东潍坊二模,3)甲、乙、丙三人中,一人是律师,一个是医生,一人是记者.已知丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是( )
A.甲是律师,乙是医生,丙是记者
B.甲是医生,乙是记者,丙是律师
C.甲是医生,乙是律师,丙是记者
D.甲是记者,乙是医生,丙是律师
答案 C
解析 由甲的年龄和记者不同,记者的年龄比乙小,得到丙是记者,从而排除B和D;由丙的年龄比医生大且比乙小,得到乙不是医生,从而乙是律师,甲是医生.故选C.
16.甲、乙、丙、丁四位同学参加一次数学智力竞赛,决出了第一名到第四名的四个名次.甲说:“我不是第一名”;乙说:“丁是第一名”;丙说:“乙是第一名”;丁说:“我不是第一名”.成绩公布后,发现这四位同学中只有一位说的是正确的.则获得第一名的同学为( )
A.甲 B.乙 C.丙 D.丁
答案 A
解析 当甲获得第一名时,甲、乙、丙说的都是错的,丁说的是对的,符合条件;
当乙获得第一名时,甲、丙、丁说的都是对的,乙说的是错的,不符合条件;
当丙获得第一名时,甲和丁说的都是对的,乙、丙说的是错的,不符合条件;
当丁获得第一名时,甲和乙说的都是对的,丙、丁说的是错的,不符合条件,故选A.
17.(2020安徽马鞍山二模,16)根据疾病防控的需要,某医院要从感染科抽调两名医生随省医疗队赴武汉参加抗疫工作,现有甲、乙、丙、丁、戊五名优秀医生申请作为志愿者参加.为确定最终驰援武汉的人选,医院领导组五位成员先各推荐两名人员,分别为“丁、戊”“丙、戊”“甲、乙”“乙、戊”“甲、丁”.根据最终入选名单发现五位领导中有一人推荐的两人都没有入选,其余四人推荐的人选中各有一人入选.根据以上信息判断,最后随省医疗队参加抗疫的两名医生分别是 .
答案 乙、丁
解析 五位领导中有一人推荐的两人都没有入选,其余四人推荐的人选中各有一人入选.
设“丁、戊”两人都没入选,那么不含丁、戊的人选组合中还剩“甲、乙”,
这与其余四人推荐的人选中各有一人入选矛盾.
设“丙、戊”两人都没入选,那么不含丙、戊的人选组合中还剩“甲、乙”和“甲、丁”,由题意这两个组合中各有一人入选,则为“乙、丁”,这符合题意,故答案为乙、丁.
同课章节目录
