专题一 1.2 函数、方程与不等式组合练 课件(共22张PPT)
文档属性
| 名称 | 专题一 1.2 函数、方程与不等式组合练 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 07:03:21 | ||
图片预览









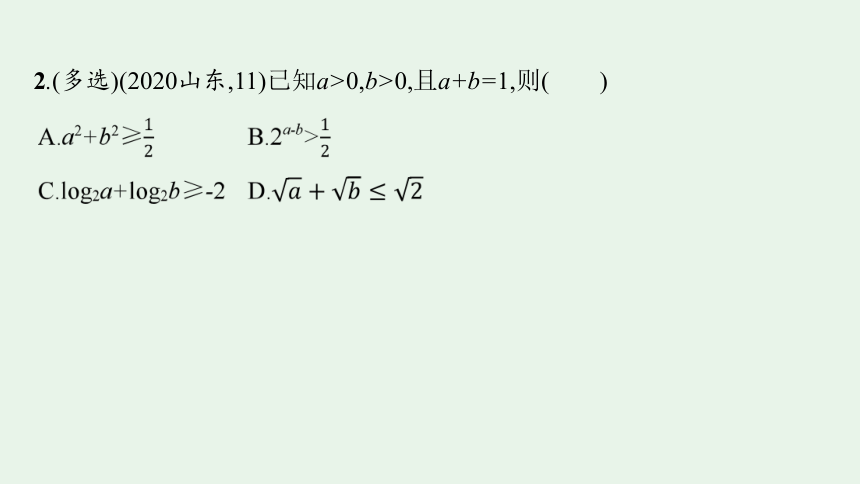
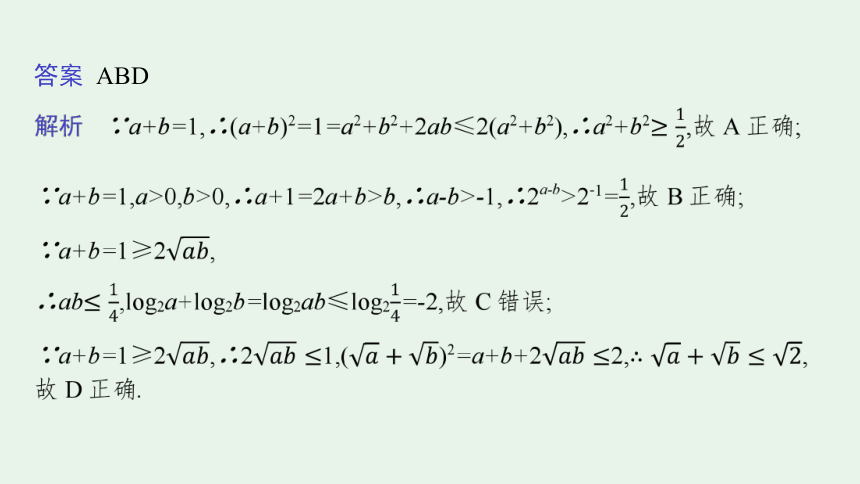

文档简介
(共33张PPT)
1.2 函数、方程与不等式组合练
第三部分
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.对于不等式a>b,c>0 ac>bc;a>b,c<0 acb>0,c>d>0 ac>bd.
2.当a>0,b>0时, ,当且仅当a=b时取等号.
3.二次函数的一般式:f(x)=ax2+bx+c(a≠0),其图象是以x=- 为对称轴的抛物线;顶点式f(x)=a(x-h)2+k(a≠0),(h,k)为顶点坐标;零点式f(x)=a(x-x1)(x-x2)
(a≠0),x1,x2为零点.
4.若ax2+bx+c=0(a≠0)的两个不相等实根为x1,x2,则
5.求二次不等式ax2+bx+c>0(或<0)(a≠0)的解集,先求其对应二次方程的根,再结合其对应的二次函数的图象确定解的范围.
6.恒成立问题的转化:a>f(x)恒成立 a>f(x)max;a≤f(x)恒成立 a≤f(x)min.
7.能成立问题的转化:a>f(x)能成立 a>f(x)min;a≤f(x)能成立 a≤f(x)max.
考向训练 限时通关
考向一
不等式的性质与基本不等式
1.(2020北京海淀一模,4)已知实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.b-aD.|b|c<|a|c
答案 D
解析 (方法一)根据数轴可得c|b|>|a|,
对于A,因为cb,则c+a对于B,因为c|b|>|a|,
所以c2>b2>a2,且b2>ab,
所以c2>b2>ab,且c2>ab,故B错误;
(方法二)不妨令c=-5,b=-4,a=-1,则c+a=-6c2=25>ab=4,故B错误;
故选D.
2.(多选)(2020山东,11)已知a>0,b>0,且a+b=1,则( )
答案 ABD
3.(多选)(2020山东青岛5月模拟,9)设a,b,c为实数,且a>b>0,则下列不等式中正确的是( )
A.log2(ab)>log2b2
B.ac2>bc2
答案 AC
解析 由a>b>0,得ab>b2,所以log2(ab)>log2b2,故A正确;
因为c2≥0,当c2=0时,选项B不成立,故B不正确;
4.(2020江苏,12)已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
答案 4
考向二
二次函数的图象与性质
6.已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是( )
A.(-∞,-1) B.(-1,2]
C.[-1,2] D.[2,5]
答案 C
解析 f(x)=-x2+4x=-(x-2)2+4.当x=2时,f(x)max=f(2)=4
由f(x)=-x2+4x=-5,得x=5或x=-1 所以要使f(x)在[m,5]上的值域是[-5,4],
则-1≤m≤2
7.(2020江西名校大联考,理6)已知函数f(x)= 在R上为增函数,则实数a的取值范围是( )
A.(-∞,1] B.[1,+∞)
C.(-∞,2] D.[2,+∞)
答案 D
8.(多选)(2020山东联考,9)已知函数f(x)=x2-2x+a有两个零点x1,x2,以下结论正确的是( )
A.a<1
C.f(-1)=f(3)
D.函数y=f(|x|)有四个零点
答案 ABC
解析 对于A,因为f(x)=x2-2x+a有两个零点,所以判别式Δ=(-2)2-4a>0,解得a<1,故A正确;
对于B,根据韦达定理有x1+x2=2,x1x2=a,所以 ,故B正确;
对于C,因为f(-1)=3+a,f(3)=3+a,所以f(-1)=f(3)成立,故C正确;
对于D,当a=0时,y=f(|x|)=|x|2-2|x|=|x|(|x|-2)=0有三根,x=0,±2,故D错误.故选ABC.
考向三
二次函数与二次不等式
9.已知函数f(x)=x2+6x+1,若关于x的不等式f(x)答案 (-4,+∞)
解析 关于x的不等式f(x)f(x)max,由函数f(x)=x2+6x+1图象的对称轴为x=-3,知当x=-5时,f(x)max=f(-5)=-4.
则实数m的取值范围是(-4,+∞).
10.(多选)(2020江苏期末,3)已知函数f(x)=x2-4x+3,则f(x)≥0的充分不必要条件是( )
A.[1,3] B.{1,3}
C.(-∞,1]∪[3,+∞) D.(3,4)
答案 BD
解析 因为f(x)≥0即x2-4x+3≥0的解集为{x|x≥3,或x≤1},
所以f(x)≥0的充分不必要条件应是{x|x≥3,或x≤1}的真子集,
所以{1,3},(3,4)满足条件.故选BD.
11.设对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,则实数a的取值范围是( )
答案 B
解析 设f(x)=x2+ax-3a,∵对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,
12.(2020四川高考模拟,理16)已知f(x)是R上的偶函数,且当x≥0时,
f(x)=|x2-3x|,则不等式f(x-2)≤2的解集为 .
解析 当x≥0时,f(x)=|x2-3x|,当0≤x≤3时,f(x)=-x2+3x,
解f(x)≤2,即-x2+3x≤2,得x≤1或x≥2,∴0≤x≤1或2≤x≤3.
考向四
二次函数、方程、不等式的综合
13.已知在(-∞,1]上递减的函数f(x)=x2-2tx+1,且对任意的x1,x2∈[0,t+1],总有|f(x1)-f(x2)|≤2,则实数t的取值范围是( )
答案 B
解析 由于f(x)=x2-2tx+1的图象的对称轴为x=t,又因为y=f(x)在(-∞,1]上是减函数,所以t≥1.
14.已知二次函数f(x)=2ax2-ax+1(a<0),若x1A.f(x1)=f(x2)
B.f(x1)>f(x2)
C.f(x1)D.与a值有关
答案 C
15.(多选)已知关于x的方程x2+(m-3)x+m=0,下列结论正确的是( )
A.方程x2+(m-3)x+m=0有实数根的充要条件是m∈{m|m<1,或m>9}
B.方程x2+(m-3)x+m=0有一正一负根的充要条件是m∈{m|m<0}
C.方程x2+(m-3)x+m=0有两正实数根的充要条件是m∈{m│0D.方程x2+(m-3)x+m=0无实数根的必要条件是m∈{m|m>1}
答案 BCD
解析 在A中,由Δ=(m-3)2-4m≥0得,m≤1或m≥9,故A错误;
在B中,当x=0时,函数y=x2+(m-3)x+m的值为m,由二次函数的图象知,方程有一正一负根的充要条件是m∈{m|m<0},故B正确;
在D中,由Δ=(m-3)2-4m<0得,11},故D正确.故选BCD.
16.(2020安徽临泉一中月考,16)已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1,设f(x)= .若不等式f(2x)-k·2x≥0在区间[-1,1]上恒成立,则实数k的取值范围是 .
答案 (-∞,0]
1.2 函数、方程与不等式组合练
第三部分
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.对于不等式a>b,c>0 ac>bc;a>b,c<0 ac
2.当a>0,b>0时, ,当且仅当a=b时取等号.
3.二次函数的一般式:f(x)=ax2+bx+c(a≠0),其图象是以x=- 为对称轴的抛物线;顶点式f(x)=a(x-h)2+k(a≠0),(h,k)为顶点坐标;零点式f(x)=a(x-x1)(x-x2)
(a≠0),x1,x2为零点.
4.若ax2+bx+c=0(a≠0)的两个不相等实根为x1,x2,则
5.求二次不等式ax2+bx+c>0(或<0)(a≠0)的解集,先求其对应二次方程的根,再结合其对应的二次函数的图象确定解的范围.
6.恒成立问题的转化:a>f(x)恒成立 a>f(x)max;a≤f(x)恒成立 a≤f(x)min.
7.能成立问题的转化:a>f(x)能成立 a>f(x)min;a≤f(x)能成立 a≤f(x)max.
考向训练 限时通关
考向一
不等式的性质与基本不等式
1.(2020北京海淀一模,4)已知实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.b-a
答案 D
解析 (方法一)根据数轴可得c
对于A,因为c
所以c2>b2>a2,且b2>ab,
所以c2>b2>ab,且c2>ab,故B错误;
(方法二)不妨令c=-5,b=-4,a=-1,则c+a=-6
故选D.
2.(多选)(2020山东,11)已知a>0,b>0,且a+b=1,则( )
答案 ABD
3.(多选)(2020山东青岛5月模拟,9)设a,b,c为实数,且a>b>0,则下列不等式中正确的是( )
A.log2(ab)>log2b2
B.ac2>bc2
答案 AC
解析 由a>b>0,得ab>b2,所以log2(ab)>log2b2,故A正确;
因为c2≥0,当c2=0时,选项B不成立,故B不正确;
4.(2020江苏,12)已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
答案 4
考向二
二次函数的图象与性质
6.已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是( )
A.(-∞,-1) B.(-1,2]
C.[-1,2] D.[2,5]
答案 C
解析 f(x)=-x2+4x=-(x-2)2+4.当x=2时,f(x)max=f(2)=4
由f(x)=-x2+4x=-5,得x=5或x=-1 所以要使f(x)在[m,5]上的值域是[-5,4],
则-1≤m≤2
7.(2020江西名校大联考,理6)已知函数f(x)= 在R上为增函数,则实数a的取值范围是( )
A.(-∞,1] B.[1,+∞)
C.(-∞,2] D.[2,+∞)
答案 D
8.(多选)(2020山东联考,9)已知函数f(x)=x2-2x+a有两个零点x1,x2,以下结论正确的是( )
A.a<1
C.f(-1)=f(3)
D.函数y=f(|x|)有四个零点
答案 ABC
解析 对于A,因为f(x)=x2-2x+a有两个零点,所以判别式Δ=(-2)2-4a>0,解得a<1,故A正确;
对于B,根据韦达定理有x1+x2=2,x1x2=a,所以 ,故B正确;
对于C,因为f(-1)=3+a,f(3)=3+a,所以f(-1)=f(3)成立,故C正确;
对于D,当a=0时,y=f(|x|)=|x|2-2|x|=|x|(|x|-2)=0有三根,x=0,±2,故D错误.故选ABC.
考向三
二次函数与二次不等式
9.已知函数f(x)=x2+6x+1,若关于x的不等式f(x)
解析 关于x的不等式f(x)
则实数m的取值范围是(-4,+∞).
10.(多选)(2020江苏期末,3)已知函数f(x)=x2-4x+3,则f(x)≥0的充分不必要条件是( )
A.[1,3] B.{1,3}
C.(-∞,1]∪[3,+∞) D.(3,4)
答案 BD
解析 因为f(x)≥0即x2-4x+3≥0的解集为{x|x≥3,或x≤1},
所以f(x)≥0的充分不必要条件应是{x|x≥3,或x≤1}的真子集,
所以{1,3},(3,4)满足条件.故选BD.
11.设对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,则实数a的取值范围是( )
答案 B
解析 设f(x)=x2+ax-3a,∵对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,
12.(2020四川高考模拟,理16)已知f(x)是R上的偶函数,且当x≥0时,
f(x)=|x2-3x|,则不等式f(x-2)≤2的解集为 .
解析 当x≥0时,f(x)=|x2-3x|,当0≤x≤3时,f(x)=-x2+3x,
解f(x)≤2,即-x2+3x≤2,得x≤1或x≥2,∴0≤x≤1或2≤x≤3.
考向四
二次函数、方程、不等式的综合
13.已知在(-∞,1]上递减的函数f(x)=x2-2tx+1,且对任意的x1,x2∈[0,t+1],总有|f(x1)-f(x2)|≤2,则实数t的取值范围是( )
答案 B
解析 由于f(x)=x2-2tx+1的图象的对称轴为x=t,又因为y=f(x)在(-∞,1]上是减函数,所以t≥1.
14.已知二次函数f(x)=2ax2-ax+1(a<0),若x1
B.f(x1)>f(x2)
C.f(x1)
答案 C
15.(多选)已知关于x的方程x2+(m-3)x+m=0,下列结论正确的是( )
A.方程x2+(m-3)x+m=0有实数根的充要条件是m∈{m|m<1,或m>9}
B.方程x2+(m-3)x+m=0有一正一负根的充要条件是m∈{m|m<0}
C.方程x2+(m-3)x+m=0有两正实数根的充要条件是m∈{m│0
答案 BCD
解析 在A中,由Δ=(m-3)2-4m≥0得,m≤1或m≥9,故A错误;
在B中,当x=0时,函数y=x2+(m-3)x+m的值为m,由二次函数的图象知,方程有一正一负根的充要条件是m∈{m|m<0},故B正确;
在D中,由Δ=(m-3)2-4m<0得,1
16.(2020安徽临泉一中月考,16)已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1,设f(x)= .若不等式f(2x)-k·2x≥0在区间[-1,1]上恒成立,则实数k的取值范围是 .
答案 (-∞,0]
同课章节目录
