专题四 4.1 数列小题专项练 课件(共33张PPT)
文档属性
| 名称 | 专题四 4.1 数列小题专项练 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:52:11 | ||
图片预览





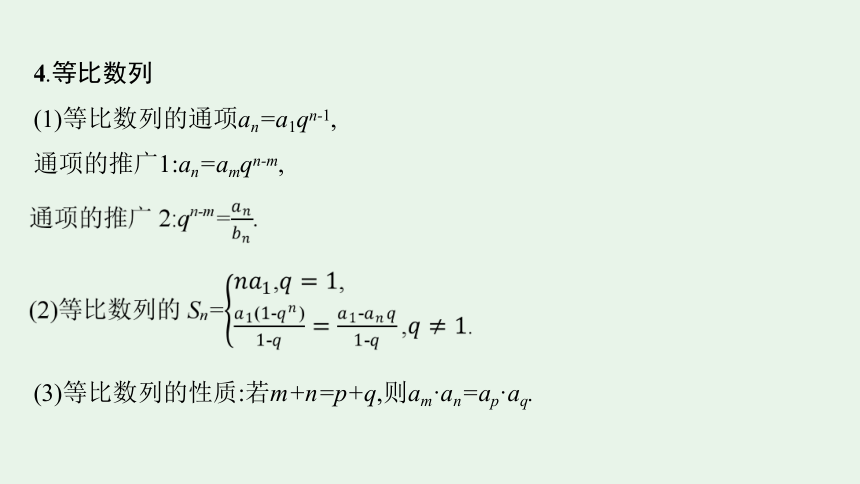






文档简介
(共33张PPT)
4.1 数列小题专项练
第三部分
考 情 分 析 从2020年新高考全国卷和2020年山东新高考模拟卷对数列的考查来看,数列在高考中考查的力度在增强.这是由于新高考试题删除了选做题,使数列成为新高考六大解答题的必选内容,高考对数列命题的“一大一小或一大”的趋势比较明显,数列题和三角函数及解三角形题会交替处在解答题的第一题或第二题的位置上,考查难度处在中等,这两个题目会有一道题设计成是“结构不良”试题,这种新题型的条件具有开放性,给考生以更多的选择性.数列题考查的重点仍是等差、等比数列的基本内容以及数列的通项、求和.在核心素养考查上主要是逻辑推理和数学运算.
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.数列的本质:定义域为N*(或它的有限子集{1,2,…,n})的函数.
3.等差数列
(1)等差数列的通项an=a1+(n-1)d,
通项的推广1:an=am+(n-m)d,
4.等比数列
(1)等比数列的通项an=a1qn-1,
通项的推广1:an=amqn-m,
(3)等比数列的性质:若m+n=p+q,则am·an=ap·aq.
考向训练 限时通关
考向一
数列及与其有关的概念
1.(2020河北武邑校级联考,理4)大衍数列来源于我国古代文献《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释我国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程中曾经经历的两仪数量总和.已知数列前10项是0,2,4,8,12,18,24,32,40,50,则大衍数列中奇数项的通项公式为( )
答案 B
解析 由数列的第一项为0,可知D错;因为数列的第三项为4,将n=3代入选项A,得到3,故A错;将n=3代入选项C,得到2,故C错;将n=3代入选项B,得到4,故B正确.
2.(2020辽宁大连24中一模,8)数列{an}满足对任意的n∈N*,均有an+an+1+an+2为定值.若a7=2,a9=3,a98=4,则数列{an}的前100项的和S100=( )
A.132 B.299 C.68 D.99
答案 B
解析 对任意的n∈N*,均有an+an+1+an+2为定值,
∴(an+1+an+2+an+3)-(an+an+1+an+2)=0,故an+3=an,
∴{an}是以3为周期的数列,
故a1=a7=2,a2=a98=4,a3=a9=3,
∴S100=(a1+a2+a3)+…+(a97+a98+a99)+a100
=33(a1+a2+a3)+a1=33×(2+4+3)+2=299.
3.(2020山东烟台一模,14)已知数列{an}的前n项和公式为Sn=2n2-n+1,则数列{an}的通项公式为 .
解析 由题意知,当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2-n-2(n-1)2+n-1=4n-3.
4.(2020全国Ⅰ,文16)数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则a1= .
答案 7
解析 当n为偶数时,有an+2+an=3n-1,则(a2+a4)+(a6+a8)+(a10+a12)+(a14+a16)=5+17+29+41=92,
因为前16项和为540,所以a1+a3+a5+a7+a9+a11+a13+a15=448.
当n为奇数时,有an+2-an=3n-1,
考向二
等差数列的基本运算
5.(2020北京人大附中二模,6)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5 B.an=3n-10
C.Sn=2n2-8n D.Sn= n2-2n
答案 A
6.(2020全国Ⅱ,理4)北京天坛的圆丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )
A.3 699块 B.3 474块
C.3 402块 D.3 339块
答案 C
解析 由题意可知,从上到下,从内到外,每环的扇面形石板数构成以9为首项,9为公差的等差数列,设为{an}.
设上层有n环,则上层扇面形石板总数为Sn,中层扇面形石板总数为S2n-Sn,下层扇面形石板总数为S3n-S2n,三层扇面形石板总数为S3n.因为{an}为等差数列,所以Sn,S2n-Sn,S3n-S2n构成等差数列,公差为9n2.因为下层比中层多729块,所以9n2=729,解得n=9.所以S3n=S27=27×9+ 9=3 402.故选C.
7.(多选)下列关于等差数列的命题中正确的有( )
A.若a,b,c成等差数列,则a2,b2,c2一定成等差数列
B.若a,b,c成等差数列,则2a,2b,2c可能成等差数列
C.若a,b,c成等差数列,则ka+2,kb+2,kc+2一定成等差数列
答案 BCD
解析 对于A,取a=1,b=2,c=3,得a2=1,b2=4,c2=9,所以a2,b2,c2不成等差数列,故A错;
对于B,取a=b=c,可得2a=2b=2c,故B正确;
对于C,由题意a+c=2b,所以(ka+2)+(kc+2)=k(a+c)+4=2(kb+2),即ka+2,kb+2,kc+2成等差数列,故C正确;
8.(2020北京,8)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),则数列{Tn}( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
答案 B
9.(2020全国Ⅱ,文14)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10= .
答案 25
解析 设等差数列{an}的公差为d.
∵a1=-2,∴a2+a6=a1+d+a1+5d=2a1+6d=-4+6d=2,解得d=1.
考向三
等比数列的基本运算
10.(2020辽宁锦州一模,7)已知等比数列{an}中,若a5+a7=8,则a4(a6+2a8)+a3a11的值为( )
A.128 B.64 C.16 D.8
答案 B
11.(2020全国Ⅱ,文6)记Sn为等比数列{an}的前n项和.若a5-a3=12,a6-a4=24,
A.2n-1 B.2-21-n
C.2-2n-1 D.21-n-1
答案 B
12.(多选)数列{an}满足an=qn(q>0,n∈N*),则以下结论正确的是( )
答案 AD
13.(2020山东淄博一模,14)记Sn为数列{an}的前n项和,若an= -1,则S7= .
答案 -254
考向四
等差、等比数列的综合
14.(2020河南郑州二模,10)已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则 的最小值为( )
A.4 B.3 C.2 -2 D.2
答案 D
15.(2020江苏,11)设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*),则d+q的值是 .
答案 4
解析 由等差数列的前n项和公式和等比数列的前n项和公式得
对照已知条件Sn=n2-n+2n-1,得d=2,q=2,所以d+q=4.
16.(多选)(2020山东青岛5月模拟,10)已知等差数列{an}的前n项和为Sn(n∈N*),公差d≠0,S6=90,a7是a3与a9的等比中项,则下列选项正确的是( )
A.a1=22
B.d=-2
C.n=10或n=11时,Sn取得最大值
D.当Sn>0时,n的最大值为20
答案 BCD
4.1 数列小题专项练
第三部分
考 情 分 析 从2020年新高考全国卷和2020年山东新高考模拟卷对数列的考查来看,数列在高考中考查的力度在增强.这是由于新高考试题删除了选做题,使数列成为新高考六大解答题的必选内容,高考对数列命题的“一大一小或一大”的趋势比较明显,数列题和三角函数及解三角形题会交替处在解答题的第一题或第二题的位置上,考查难度处在中等,这两个题目会有一道题设计成是“结构不良”试题,这种新题型的条件具有开放性,给考生以更多的选择性.数列题考查的重点仍是等差、等比数列的基本内容以及数列的通项、求和.在核心素养考查上主要是逻辑推理和数学运算.
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.数列的本质:定义域为N*(或它的有限子集{1,2,…,n})的函数.
3.等差数列
(1)等差数列的通项an=a1+(n-1)d,
通项的推广1:an=am+(n-m)d,
4.等比数列
(1)等比数列的通项an=a1qn-1,
通项的推广1:an=amqn-m,
(3)等比数列的性质:若m+n=p+q,则am·an=ap·aq.
考向训练 限时通关
考向一
数列及与其有关的概念
1.(2020河北武邑校级联考,理4)大衍数列来源于我国古代文献《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释我国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程中曾经经历的两仪数量总和.已知数列前10项是0,2,4,8,12,18,24,32,40,50,则大衍数列中奇数项的通项公式为( )
答案 B
解析 由数列的第一项为0,可知D错;因为数列的第三项为4,将n=3代入选项A,得到3,故A错;将n=3代入选项C,得到2,故C错;将n=3代入选项B,得到4,故B正确.
2.(2020辽宁大连24中一模,8)数列{an}满足对任意的n∈N*,均有an+an+1+an+2为定值.若a7=2,a9=3,a98=4,则数列{an}的前100项的和S100=( )
A.132 B.299 C.68 D.99
答案 B
解析 对任意的n∈N*,均有an+an+1+an+2为定值,
∴(an+1+an+2+an+3)-(an+an+1+an+2)=0,故an+3=an,
∴{an}是以3为周期的数列,
故a1=a7=2,a2=a98=4,a3=a9=3,
∴S100=(a1+a2+a3)+…+(a97+a98+a99)+a100
=33(a1+a2+a3)+a1=33×(2+4+3)+2=299.
3.(2020山东烟台一模,14)已知数列{an}的前n项和公式为Sn=2n2-n+1,则数列{an}的通项公式为 .
解析 由题意知,当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2-n-2(n-1)2+n-1=4n-3.
4.(2020全国Ⅰ,文16)数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则a1= .
答案 7
解析 当n为偶数时,有an+2+an=3n-1,则(a2+a4)+(a6+a8)+(a10+a12)+(a14+a16)=5+17+29+41=92,
因为前16项和为540,所以a1+a3+a5+a7+a9+a11+a13+a15=448.
当n为奇数时,有an+2-an=3n-1,
考向二
等差数列的基本运算
5.(2020北京人大附中二模,6)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5 B.an=3n-10
C.Sn=2n2-8n D.Sn= n2-2n
答案 A
6.(2020全国Ⅱ,理4)北京天坛的圆丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )
A.3 699块 B.3 474块
C.3 402块 D.3 339块
答案 C
解析 由题意可知,从上到下,从内到外,每环的扇面形石板数构成以9为首项,9为公差的等差数列,设为{an}.
设上层有n环,则上层扇面形石板总数为Sn,中层扇面形石板总数为S2n-Sn,下层扇面形石板总数为S3n-S2n,三层扇面形石板总数为S3n.因为{an}为等差数列,所以Sn,S2n-Sn,S3n-S2n构成等差数列,公差为9n2.因为下层比中层多729块,所以9n2=729,解得n=9.所以S3n=S27=27×9+ 9=3 402.故选C.
7.(多选)下列关于等差数列的命题中正确的有( )
A.若a,b,c成等差数列,则a2,b2,c2一定成等差数列
B.若a,b,c成等差数列,则2a,2b,2c可能成等差数列
C.若a,b,c成等差数列,则ka+2,kb+2,kc+2一定成等差数列
答案 BCD
解析 对于A,取a=1,b=2,c=3,得a2=1,b2=4,c2=9,所以a2,b2,c2不成等差数列,故A错;
对于B,取a=b=c,可得2a=2b=2c,故B正确;
对于C,由题意a+c=2b,所以(ka+2)+(kc+2)=k(a+c)+4=2(kb+2),即ka+2,kb+2,kc+2成等差数列,故C正确;
8.(2020北京,8)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),则数列{Tn}( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
答案 B
9.(2020全国Ⅱ,文14)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10= .
答案 25
解析 设等差数列{an}的公差为d.
∵a1=-2,∴a2+a6=a1+d+a1+5d=2a1+6d=-4+6d=2,解得d=1.
考向三
等比数列的基本运算
10.(2020辽宁锦州一模,7)已知等比数列{an}中,若a5+a7=8,则a4(a6+2a8)+a3a11的值为( )
A.128 B.64 C.16 D.8
答案 B
11.(2020全国Ⅱ,文6)记Sn为等比数列{an}的前n项和.若a5-a3=12,a6-a4=24,
A.2n-1 B.2-21-n
C.2-2n-1 D.21-n-1
答案 B
12.(多选)数列{an}满足an=qn(q>0,n∈N*),则以下结论正确的是( )
答案 AD
13.(2020山东淄博一模,14)记Sn为数列{an}的前n项和,若an= -1,则S7= .
答案 -254
考向四
等差、等比数列的综合
14.(2020河南郑州二模,10)已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则 的最小值为( )
A.4 B.3 C.2 -2 D.2
答案 D
15.(2020江苏,11)设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*),则d+q的值是 .
答案 4
解析 由等差数列的前n项和公式和等比数列的前n项和公式得
对照已知条件Sn=n2-n+2n-1,得d=2,q=2,所以d+q=4.
16.(多选)(2020山东青岛5月模拟,10)已知等差数列{an}的前n项和为Sn(n∈N*),公差d≠0,S6=90,a7是a3与a9的等比中项,则下列选项正确的是( )
A.a1=22
B.d=-2
C.n=10或n=11时,Sn取得最大值
D.当Sn>0时,n的最大值为20
答案 BCD
同课章节目录
