第四部分 一、考前必记的50个知识点 课件(共91张PPT)
文档属性
| 名称 | 第四部分 一、考前必记的50个知识点 课件(共91张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:53:01 | ||
图片预览











文档简介
(共91张PPT)
一、考前必记的50个知识点
第四部分
1.集合
(1)集合间关系的两个重要结论
①A B包含A=B和A B两种情况,两者必居其一,若存在x∈B且x A,说明A≠B,只能是A B.
②集合相等的两层含义:若A B且B A,则A=B;若A=B,则A B且B A .
提醒①任何一个集合是它本身的子集,即A A.
②含有n个元素的集合有2n个子集,有2n-1个真子集,有2n-2个非空真子集.
(2)集合之间关系的判断方法
①A B A B且A≠B,类比于a②A B A B或A=B,类比于a≤b a③A=B A B且A B,类比于a=b a≤b且a≥b.
(3)集合中元素的三大特性:确定性、互异性、无序性.
(4)集合之间的运算:A∪B=B A∩B=A A B时,不要忽略A= 的情况;A∩B= 时,不要忽略A= 或B= .
2.常见关键词及其否定形式
关键 词 等于 大于 小于 是 一定 是 都是 至少有 一个 至多 有一个 存在
否定 词 不等于 不大于 不小于 不是 不一 定是 不都是 一个也 没有 至少 有两个 不存在
3.充分、必要条件
记p,q对应的集合分别为A,B,则有
①A B,p是q的充分不必要条件;
②A B,p是q的必要不充分条件;
③A=B,p是q的充要条件;
④A B且A B,p是q的既不充分也不必要条件.
4.函数的定义域及相关的6个结论
(1)如果f(x)是整式函数,那么函数的定义域是R.
(2)如果f(x)是分式函数,那么函数的定义域是使分母不等于0的实数的集合.
(3)如果f(x)是偶次根式函数,那么函数的定义域是使被开方数大于或等于0的实数的集合.
(4)如果f(x)是对数函数,那么函数的定义域是使真数大于0的实数的集合.
(5)如果f(x)是由几个代数式构成的,那么函数的定义域是使各式子都有意义的实数的集合.
(6)如果f(x)是从实际问题中得出的函数,则要结合实际情况考虑函数的定义域.
5.函数的值域
求函数值域常用的7种方法
(1)配方法:二次函数及能通过换元法转化为二次函数的函数类型.
(2)判别式法:分子、分母中含有二次项的函数类型,此函数经过变形后可以化为x2A(y)+xB(y)+C(y)=0的形式,再利用判别式加以判断.
6.函数奇偶性的性质
(1)f(x)是偶函数 f(-x)=f(x)=f(|x|);
(2)f(x)是奇函数 f(-x)=-f(x);
(3)定义域含0的奇函数满足f(0)=0.
7.函数周期性的几个结论
由“函数f(x)满足f(x)=f(a+x)(a≠0),则f(x)是周期为a的周期函数”得:
(1)函数f(x)满足-f(x)=f(a+x)(a≠0),则f(x)是周期T=2a的周期函数;
(4)若f(x+a)=f(x-a)(a≠0)成立,则T=2a.
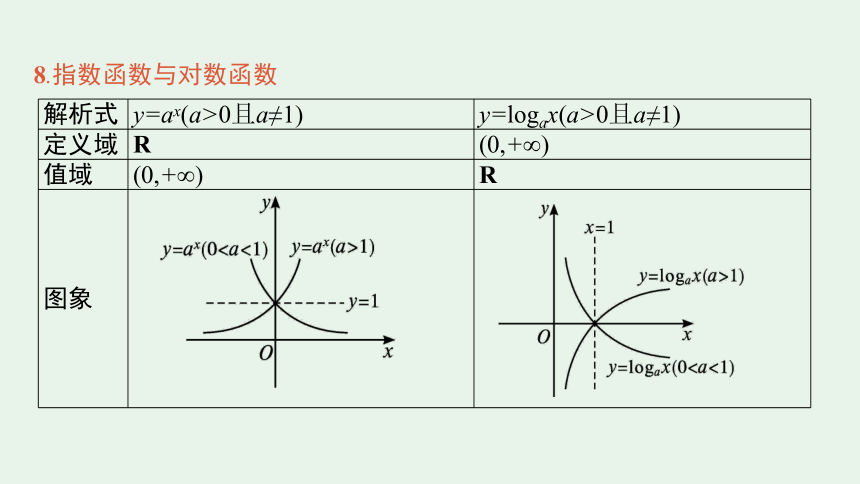
8.指数函数与对数函数
解析式 y=ax(a>0且a≠1) y=logax(a>0且a≠1)
定义域 R (0,+∞)
值域 (0,+∞) R
图象
关系 互为反函数
奇偶性 非奇非偶 非奇非偶
单调性 当01时,在R上是增函数 当0当a>1时,在(0,+∞)上是增函数
提醒直线x=1与所给指数函数图象的交点的纵坐标即为底数值,直线y=1与所给对数函数图象的交点的横坐标即为底数值.
9.函数零点的判断方法
(1)利用零点存在定理判断法:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0.这个c也就是方程f(x)=0的根.口诀:函数零点方程根,数形本是同根生,函数零点端点判,图象连续不能忘.
(2)代数法:求方程f(x)=0的实数根.
(3)几何法:对于不能用求根公式的方程,可以将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点.
10.导数
(1)基本初等函数的导数公式
①(sin x)'=cos x,(cos x)'=-sin x.
③(ex)'=ex,(ax)'=axln a(a>0,且a≠1).
(2)导数的四则运算法则
①(u±v)'=u'±v'.
②(uv)'=vu'+v'u (cv)'=cv'(c为常数).
提醒(1)若两个函数可导,则它们的和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
(2)利用公式求导时,一定要注意公式的适用范围及符号,如(xn)'=nxn-1中n∈Q,(cos x)'=-sin x.
(3)注意公式不要用混,如(ax)'=axln a,而不是(ax)'=xax-1.
(4)导数的加法与减法法则,可由两个可导函数推广到任意有限个可导函数的情形,即[u(x)±v(x)±…±w(x)]'=u'(x)±v'(x)±…±w'(x).
(5)一般情况下,[f(x)g(x)]'≠f'(x)g'(x),[f(x)·g(x)]'≠f'(x)+g'(x),
11.利用导数判断函数的单调性:设函数y=f(x)在某个区间内可导,如果f'(x)>0,那么f(x)在该区间内为增函数;如果f'(x)<0,那么f(x)在该区间内为减函数;如果在某个区间内恒有f'(x)=0,那么f(x)在该区间内为常函数.
12.极值与最值
(1)判断极大、极小值的方法
当函数f(x)在点x0处连续时,
①如果在x0附近的左侧f'(x)>0,右侧f'(x)<0,则f(x0)是极大值.
②如果在x0附近的左侧f'(x)<0,右侧f'(x)>0,则f(x0)是极小值.
提醒(1)可导函数在极值点处的导数为0,但导数为0的点不一定是极值点,如函数f(x)=x3,x=0就不是极值点,但f'(0)=0.
(2)极值点不是一个点,而是一个数x0,当x=x0时,函数取得极值.在x0处有f'(x0)=0是函数f(x)在x0处取得极值的必要不充分条件.
(3)函数f(x)在一闭区间上的最大值是此函数在此区间上的极大值与其端点函数值中的最大值,函数f(x)在一闭区间上的最小值是此函数在此区间上的极小值与其端点函数值中的最小值.
(2)极值与最值的区别与联系
①区别:
函数的极值 函数的最值
函数的极值点一定出现在区间的内部,区间的端点不能成为极值点 使函数取得最大值,最小值的点可能在区间的内部,也可能在区间的端点
函数的极值是通过比较极值点附近的函数值得出的 函数的最值是通过比较整个定义域内的函数值得出的
函数的极值可能不止一个,也可能一个没有 函数在其定义区间上的最大值、最小值最多各有一个
函数的极大值不一定大于函数的极小值 函数的最大值一定大于函数的最小值
②联系:(ⅰ)当连续函数在开区间内的极值点只有一个时,相应的极值点必为函数的最值点;
(ⅱ)极值有可能是最值,但最值只要不在区间端点处取得,其必定是极值.
13.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
14.三角函数的诱导公式
公式一:
sin(2kπ+α)=sin α,cos(2kπ+α)=cos α,tan(2kπ+α)=tan α,k∈Z.
公式二:
sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.
公式三:
sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.
公式四:
sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.
公式五:
提醒奇变偶不变,符号看象限
“奇、偶”指的是 的倍数是奇数还是偶数.“变与不变”指的是三角函数名称的变化,“变”是指正弦变余弦(或余弦变正弦).“符号看象限”的含义是:把角α看作锐角,看n· ±α(n∈Z)是第几象限角,从而得到等式右边是正号还是负号.
15.三角函数的图象变换
(1)y=sin x的图象向左平移φ(φ>0)个单位长度得到y=sin(x+φ)的图象(当φ<0时,则向右平移|φ|个单位长度).
(2)y=sin x的图象上所有点的纵坐标保持不变,横坐标变为原来的 倍,得到y=sin ωx的图象.
(3)y=sin x的图象上所有点的横坐标保持不变,纵坐标变为原来的A倍,得到y=Asin x的图象.
提醒(1)由y=sin ωx的图象经过平移变换得到y=sin(ωx+φ)的图象,平移的单
(2)函数图象平移、伸缩变换的实质是点的变化,所以可以借助三角函数图象上特征点坐标的变化寻找平移、伸缩变换的规律,一般借助于两个函数图象上的最高点或最低点的坐标来分析.
16.三角函数的对称性
(4)求曲线y=Asin(ωx+φ)(或y=Acos(ωx+φ),y=Atan(ωx+φ))的对称中心(或对称轴),只需令ωx+φ等于对应的值,求出x即可.
17.三角恒等变换
(1)两角和与差的正弦、余弦、正切公式
sin(α±β)=sin αcos β±cos αsin β.
cos(α±β)=cos αcos β sin αsin β.
(2)二倍角公式
sin 2α=2sin αcos α.
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
18.正弦定理、余弦定理及其推论
(1)正弦定理
b=2Rsin B,c=2Rsin C a∶b∶c=sin A∶sin B∶sin C.
(2)余弦定理
a2=b2+c2-2bccos A,b2=c2+a2-2cacos B,c2=a2+b2-2abcos C.
(3)三角形内角和定理
(4)三角形面积公式
19.平面向量
(1)平面向量共线的坐标表示的两种形式
①若a=(x1,y1),b=(x2,y2),则a∥b x1y2=x2y1,此形式对任意向量a,b(b≠0)都适用.
(2)有关数量积应用的常见结论
已知非零向量a=(x1,y1),b=(x2,y2),则:
①a⊥b a·b=0 x1x2+y1y2=0.
20.等差数列
(1)等差数列的判断方法
①定义法:an+1-an=d(d为常数,n∈N*) {an}是等差数列.
②通项公式法:an=a1+(n-1)d(其中a1,d为常数,n∈N*) {an}为等差数列.
③等差中项法:2an+1=an+an+2(n∈N*) {an}是等差数列.
④前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列.
(2)等差数列前n项和的最大值、最小值的求法
①通项公式法:当a1>0,d<0时,Sn有最大值,可由an≥0且an+1≤0求得n,从而求出Sn的最大值;当a1<0,d>0时,Sn有最小值,可由an≤0且an+1≥0求得n,从而求出Sn的最小值.
②二次函数法:用求二次函数最值的方法求Sn的最值.
值得注意的是n∈N*,因此等差数列前n项和取得最值时n的值可能不是一个值,也有可能是两个值.
21.等比数列的判断方法
(3)通项公式法:an=a1qn-1(其中a1,q为非零常数,n∈N*) {an}为等比数列.
提醒判断一个数列是否是等比数列,还有一种直观的判断方法,即前n项和公式法:若Sn表示数列{an}的前n项和,且Sn=-aqn+a(a≠0,q≠0,q≠1),则数列{an}是公比为q的等比数列.但此方法不能用于证明一个数列是等比数列.
22.数列中项的最值的求法
(1)根据数列与函数之间的对应关系,构造相应的函数f(n)=an,利用求解函数最值的方法(多利用函数的单调性)进行求解,但要注意自变量的取值必须是正整数的限制.
(2)利用数列的单调性求解,由不等式an+1≥an(或an+1≤an)求解出n的取值范围,从而确定数列单调性的变化,进而确定相应的最值.
(3)转化为关于n的不等式组求解:若求数列{an}的最大项,则可解不等式组
23.不等式的解法
(1)分式不等式的解法
提醒对于解分式不等式,将分式不等式转化成整式不等式时,如果不等式是含有等号的不等式形式,则很容易忘掉分母不为0的情形,从而导致出错;另一种可能出现错误的情形是在将两边进行平方时,容易扩大或缩小不等式的范围.
(2)指数、对数不等式的解法
①解指数、对数不等式的依据是指数、对数函数的概念和性质,因而同底法是解指数、对数不等式的基本方法.当然最终的目的是将它们转化为代数不等式,其主要类型和解法有:
(ⅰ)af(x)>aφ(x) f(x)>φ(x)(a>1)或f(x)<φ(x)(0(ⅱ)logaf(x)>logaφ(x) f(x)>φ(x)>0(a>1)或0②在解对数不等式时,要注意变形的等价性;也要注意底数大于零且不等于1,真数大于零的制约因素.
(3)一元二次不等式的恒成立问题
①在实数集R上,ax2+bx+c>0(<0)恒成立,则a>0(a<0),且Δ<0,反之也成立;ax2+bx+c≥0(≤0)恒成立,则a>0(a<0),且Δ≤0,反之也成立.
②若一元二次不等式在某一区间上恒成立,则可结合相应二次函数的图象,判断函数图象在这个区间上与对称轴的相对位置,列出不等式恒成立时满足的条件即可.
③一般地,不等式恒成立问题通常转化为函数的最值问题来解决.如f(x)≤a恒成立 f(x)max≤a,f(x)≥a恒成立 f(x)min≥a.
24.基本不等式
(1)基本不等式的变形
①根式形式:a+b≥2 (a>0,b>0),当且仅当a=b时,等号成立.
(2)利用基本不等式求最值
提醒利用基本不等式求最大值、最小值时应注意“一正、二定、三相等”,即:①所求式中的相关项必须是正数;②求积xy的最大值时,要看和x+y是否为定值.求和x+y的最小值时,要看积xy是否为定值.求解时,常用到“拆项”“凑项”等解题技巧;③当且仅当各项相等时,才能取等号.以上三点应特别注意,缺一不可.
25.空间几何体的表面积和体积
(1)直棱柱的侧面积:S侧=cl(c是底面周长,l为侧棱长).
(2)柱体的体积:V柱=Sh(S为底面积,h是柱体的高).
26.球的组合体
(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长,正方体的棱切球的直径是正方体的面对角线长,正方体的外接球的直径是正方体的体对角线长.
27.证明空间位置关系的方法
提醒利用定理证明线面关系时要注意结合几何体的结构特征,尤其要注意灵活利用正棱柱、正棱锥等特殊几何体的性质,进行空间线面关系的相互转化.
28.空间向量的坐标运算
设a=(a1,a2,a3),b=(b1,b2,b3),则
(1)a·b=a1b1+a2b2+a3b3;
(2)a∥b a1=λb1,a2=λb2,a3=λb3(λ∈R,b≠0);
(3)a⊥b a1b1+a2b2+a3b3=0(b≠0);
29.空间向量的应用
(1)夹角公式:设非零向量a=(a1,a2,a3),b=(b1,b2,b3),则
提醒在处理实际问题时,要根据具体图形确定二面角的平面角是锐角还是钝角,以确定角的大小.
30.直线
(1)直线方程的5种形式
名称 方程的形式 常数的几何意义 适用范围
点斜式 y-y0=k(x-x0) (x0,y0)是直线上一定点,k是斜率 不垂直于x轴
斜截式 y=kx+b k是斜率,b是直线在y轴上的截距 不垂直于x轴
(2)两条直线的位置关系
①已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1,B1,A2,B2全不为0),则l1,l2
当A1,B1,A2,B2中有0时,应单独讨论.
②直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0垂直 A1A2+B1B2=0.
提醒讨论两条直线的位置关系时应注意斜率不存在或斜率为0的情况,当两条直线中一条直线的斜率不存在,另一条直线的斜率为0时,它们也垂直.
31.圆
(1)圆的四种方程
①圆的标准方程:(x-a)2+(y-b)2=r2(r>0).
②圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
④圆的直径式方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0(圆的直径的端点是A(x1,y1),B(x2,y2)).
(2)直线与圆的位置关系
直线l:Ax+By+C=0和圆C:(x-a)2+(y-b)2=r2(r>0)有相交、相离、相切三种情况.可从代数和几何两个方面来判断:
①代数方法(判断直线与圆的方程联立所得方程组的解的情况):Δ>0 相交;Δ<0 相离;Δ=0 相切;
②几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为d,则dr 相离;d=r 相切.
(3)圆与圆的位置关系
位置关系 几何法 代数法 公切线的条数
圆心距d与r1,r2的关系 联立两圆方程组成方程组的解的情况
外离 d>r1+r2 无解 4
外切 d=r1+r2 一组实数解 3
相交 |r1-r2|内切 d=|r1-r2|(r1≠r2) 一组实数解 1
内含 0≤d<|r1-r2|(r1≠r2) 无解 0
32.椭圆
标准方程
几 何 性 质 范围 -a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a
对称性 对称轴:x轴,y轴;对称中心:原点
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
顶点 A1(-a,0),A2(a,0); B1(0,-b),B2(0,b) A1(0,-a),A2(0,a);
B1(-b,0),B2(b,0)
轴 线段A1A2,B1B2分别是椭圆的长轴和短轴,长轴长为2a,短轴长为2b
焦距 |F1F2|=2c
离心率 焦距与长轴长的比值:e∈(0,1)
a,b,c的关系 b2=a2-c2
33.双曲线
(1)双曲线的标准方程及几何性质
几 何 性 质 范围 |x|≥a,y∈R |y|≥a,x∈R
对称性 对称轴:x轴,y轴;对称中心:原点
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为2a,虚轴长为2b
焦距 |F1F2|=2c
离心率 焦距与实轴长的比值:e∈(1,+∞)
渐近线
a,b,c的关系 b2=c2-a2
提醒①离心率e的取值范围是(1,+∞).当e越接近于1时,双曲线开口越小;当e越接近于+∞时,双曲线开口越大.
②满足||PF1|-|PF2||=2a的点P的轨迹不一定是双曲线,当2a=0时,点P的轨迹是线段F1F2的中垂线;当0<2a<|F1F2|时,点P的轨迹是双曲线;当2a=|F1F2|时,点P的轨迹是两条射线;当2a>|F1F2|时,点P的轨迹不存在.
(2)双曲线方程与渐近线方程的关系
34.抛物线
(1)抛物线的标准方程及几何性质
(2)抛物线焦点弦的常用结论
设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),α为直线AB的倾斜角,则
35.直线与圆锥曲线的位置关系
(1)弦长的求解方法
设直线与圆锥曲线交于A(x1,y1),B(x2,y2)两点,若直线AB的斜率存在(设为k),
当直线AB的斜率不存在时,可直接求出直线与圆锥曲线的交点坐标,利用两点间的距离公式求弦长.
(2)圆锥曲线中的最值问题
①利用圆锥曲线的定义进行转化,一般在三点共线时取得最值.
②求圆锥曲线上的点到已知直线的距离的最值,当已知直线的平行线与圆锥曲线相切时,两平行线间的距离即为所求.
③利用基本不等式求最值.
36.频率与概率的区别与联系
(1)区别
①频率具有随机性,在不同的试验中,同一事件发生的频率可能不同;
②概率是频率的稳定值,是一个确定的常数,不管进行多少次试验,同一事件发生的概率是不变的.
(2)联系
①频率和概率都是用来刻画随机事件发生的可能性大小的量;
②概率可看作频率在理论上的期望值,随试验次数的增加,频率可近似地作为这个事件的概率.
37.事件的关系与运算
(1)包含关系:如果事件A发生,则事件B一定发生,这时称事件B包含事件A,记作B A(或A B).
(2)相等事件:如果B A且A B,那么称事件A与事件B相等,记作A=B.
(3)并(和)事件:若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).
(4)交(积)事件:若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件),记作A∩B(或AB).
(5)互斥事件:若A∩B为不可能事件(即A∩B= ),那么称事件A与事件B互斥,其含义是事件A与事件B在任何一次试验中都不会同时发生.
(6)对立事件:若A∩B为不可能事件,A∪B为必然事件,那么称事件A与事件B互为对立事件,其含义是事件A与事件B在任何一次试验中有且只有一个发生.
提醒互斥事件与对立事件都是指两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生以外,还要求二者必须有一个发生.因此,对立事件一定是互斥事件,而互斥事件未必是对立事件.
38.概率的几个基本性质
(1)任何事件A的概率都在0~1之间,即0≤P(A)≤1.
(2)若A B,则P(A)≤P(B).
(3)必然事件发生的概率为1,不可能事件发生的概率为0.
(4)当事件A与事件B互斥时,P(A+B)=P(A)+P(B).注意没有事件A与事件B互斥这一条件时,这个公式不成立.
(5)若事件A与事件B互为对立事件,则P(A)+P(B)=1.
提醒当一事件的概率不易直接求,但其对立事件的概率易求时,可运用(5),即用间接法求概率.
39.古典概型的概率公式
如果随机事件A包含的基本事件数为m,总的基本事件数为n,则
提醒求解古典概型问题的步骤
(1)判断本次试验的结果是否是等可能的,设出所求的事件A.
(2)分别计算总的基本事件的个数n和所求的事件A所包含的基本事件的个数m.
40.均值的相关结论
(1)E(k)=k(k为常数).
(2)E(aX+b)=aE(X)+b.
(3)E(X1+X2)=E(X1)+E(X2).
(4)若X1,X2相互独立,则E(X1·X2)=E(X1)·E(X2).
(5)若随机变量X服从两点分布,则E(X)=p.
(6)若X服从二项公布,即X~B(n,p),则E(X)=np.
提醒E(X)是一个常数,由X的分布列唯一确定,它描述X取值的平均状态,作为随机变量X是可变的,可取不同的值.
41.方差的相关性质结论
(1)D(k)=0(k为常数).
(2)D(aX+b)=a2D(X).
(3)D(X)=E(X2)-[E(X)]2.
(4)若X1,X2,…,Xn两两独立,则D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn).
提醒①随机变量的方差与标准差都反映了随机变量取值的稳定与波动,集中与离散程度,其中标准差与随机变量本身有相同的单位.
②方差也是一个常数,它不具有随机性,方差的值一定是非负的.
42.二项分布与正态分布
②正态分布密度函数的性质:函数图象关于直线x=μ对称;σ(σ>0)的大小决定函数图象的“胖”“瘦”;P(μ-σ③在实际问题中进行概率、百分比计算时,关键是把正态分布的两个重要参数μ,σ求出,然后确定三个区间(范围):(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ),与已知概率值进行联系求解.
43.排列数、组合数公式及其相关性质
(1)排列数
①公式
(2)组合数
①公式
44.求解排列组合问题常用的解题方法
(1)元素相邻的排列问题——“捆绑”法.
(2)元素相间的排列问题——“插空”法.
(3)元素有顺序限制的排列问题——“除序”法,即先把这几个有顺序限制的元素及其他元素一同进行全排列,然后用总的排列数除以这几个元素的全排列数.
(4)带有“含”“不含”“至多”“至少”的组合(排列)问题——间接法,即先不考虑限制条件求出组合(排列)数,再排除不符合要求的组合(排列)数.
45.二项式定理
(2)二项式系数与项的系数是两个完全不同的概念,二项式系数与a,b的值无关,项的系数不仅与项数有关,也与a,b的值有关.
46.两种抽样法
类别 共同点 各自特点 联系 适用范围
简单随 机抽样 ①抽样过程中每个个体被抽到的可能性相等; ②每次抽出个体后不再将它放回,即不放回抽样 从总体中逐个抽取 最基本的抽样方法 总体中的个体较少
分层 抽样 将总体分成几层,分层按比例进行抽取 分层抽样时采用简单随机抽样或系统抽样 总体由差异明显的几部分组成
提醒用分层抽样法抽样时,各层抽样标准要一致,互不重叠;各层抽取的比例都等于样本容量在总体中的比例,即为
47.变量间的相关关系
线性相关系数r是从数值上来判断变量间的线性相关程度的,|r|的值越接近于1,说明变量之间的线性相关程度越高;|r|的值越接近于0,说明变量之间的线性相关程度越低.当两个变量的关系可用一次函数表示时,r=±1,若斜率为正,r=1,否则r=-1.r为正时表示正相关,r为负时表示负相关.
48.线性回归方程的求解步骤
(1)利用散点图或进行相关性检验判定两个变量具有线性相关关系.
(4)写出线性回归方程.
提醒回归直线一定经过样本点的中心( ),据此性质可以解决有关的计算问题、判断结论的正确性.
49.独立性检验的基本方法
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表如表:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
根据观测数据计算由公式K2= 所给出的随机变量K2的观测值k,并且k的值越大,说明“X与Y有关系”成立的可能性越大,可以利用数据来确定“X和Y有关系”的可信程度.
50.复数的四则运算法则
(1)(a+bi)±(c+di)=(a±c)+(b±d)i.
(2)(a+bi)(c+di)=(ac-bd)+(bc+ad)i.
提醒几个结论:①(1±i)2=±2i.
一、考前必记的50个知识点
第四部分
1.集合
(1)集合间关系的两个重要结论
①A B包含A=B和A B两种情况,两者必居其一,若存在x∈B且x A,说明A≠B,只能是A B.
②集合相等的两层含义:若A B且B A,则A=B;若A=B,则A B且B A .
提醒①任何一个集合是它本身的子集,即A A.
②含有n个元素的集合有2n个子集,有2n-1个真子集,有2n-2个非空真子集.
(2)集合之间关系的判断方法
①A B A B且A≠B,类比于a②A B A B或A=B,类比于a≤b a
(3)集合中元素的三大特性:确定性、互异性、无序性.
(4)集合之间的运算:A∪B=B A∩B=A A B时,不要忽略A= 的情况;A∩B= 时,不要忽略A= 或B= .
2.常见关键词及其否定形式
关键 词 等于 大于 小于 是 一定 是 都是 至少有 一个 至多 有一个 存在
否定 词 不等于 不大于 不小于 不是 不一 定是 不都是 一个也 没有 至少 有两个 不存在
3.充分、必要条件
记p,q对应的集合分别为A,B,则有
①A B,p是q的充分不必要条件;
②A B,p是q的必要不充分条件;
③A=B,p是q的充要条件;
④A B且A B,p是q的既不充分也不必要条件.
4.函数的定义域及相关的6个结论
(1)如果f(x)是整式函数,那么函数的定义域是R.
(2)如果f(x)是分式函数,那么函数的定义域是使分母不等于0的实数的集合.
(3)如果f(x)是偶次根式函数,那么函数的定义域是使被开方数大于或等于0的实数的集合.
(4)如果f(x)是对数函数,那么函数的定义域是使真数大于0的实数的集合.
(5)如果f(x)是由几个代数式构成的,那么函数的定义域是使各式子都有意义的实数的集合.
(6)如果f(x)是从实际问题中得出的函数,则要结合实际情况考虑函数的定义域.
5.函数的值域
求函数值域常用的7种方法
(1)配方法:二次函数及能通过换元法转化为二次函数的函数类型.
(2)判别式法:分子、分母中含有二次项的函数类型,此函数经过变形后可以化为x2A(y)+xB(y)+C(y)=0的形式,再利用判别式加以判断.
6.函数奇偶性的性质
(1)f(x)是偶函数 f(-x)=f(x)=f(|x|);
(2)f(x)是奇函数 f(-x)=-f(x);
(3)定义域含0的奇函数满足f(0)=0.
7.函数周期性的几个结论
由“函数f(x)满足f(x)=f(a+x)(a≠0),则f(x)是周期为a的周期函数”得:
(1)函数f(x)满足-f(x)=f(a+x)(a≠0),则f(x)是周期T=2a的周期函数;
(4)若f(x+a)=f(x-a)(a≠0)成立,则T=2a.
8.指数函数与对数函数
解析式 y=ax(a>0且a≠1) y=logax(a>0且a≠1)
定义域 R (0,+∞)
值域 (0,+∞) R
图象
关系 互为反函数
奇偶性 非奇非偶 非奇非偶
单调性 当0
提醒直线x=1与所给指数函数图象的交点的纵坐标即为底数值,直线y=1与所给对数函数图象的交点的横坐标即为底数值.
9.函数零点的判断方法
(1)利用零点存在定理判断法:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0.这个c也就是方程f(x)=0的根.口诀:函数零点方程根,数形本是同根生,函数零点端点判,图象连续不能忘.
(2)代数法:求方程f(x)=0的实数根.
(3)几何法:对于不能用求根公式的方程,可以将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点.
10.导数
(1)基本初等函数的导数公式
①(sin x)'=cos x,(cos x)'=-sin x.
③(ex)'=ex,(ax)'=axln a(a>0,且a≠1).
(2)导数的四则运算法则
①(u±v)'=u'±v'.
②(uv)'=vu'+v'u (cv)'=cv'(c为常数).
提醒(1)若两个函数可导,则它们的和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
(2)利用公式求导时,一定要注意公式的适用范围及符号,如(xn)'=nxn-1中n∈Q,(cos x)'=-sin x.
(3)注意公式不要用混,如(ax)'=axln a,而不是(ax)'=xax-1.
(4)导数的加法与减法法则,可由两个可导函数推广到任意有限个可导函数的情形,即[u(x)±v(x)±…±w(x)]'=u'(x)±v'(x)±…±w'(x).
(5)一般情况下,[f(x)g(x)]'≠f'(x)g'(x),[f(x)·g(x)]'≠f'(x)+g'(x),
11.利用导数判断函数的单调性:设函数y=f(x)在某个区间内可导,如果f'(x)>0,那么f(x)在该区间内为增函数;如果f'(x)<0,那么f(x)在该区间内为减函数;如果在某个区间内恒有f'(x)=0,那么f(x)在该区间内为常函数.
12.极值与最值
(1)判断极大、极小值的方法
当函数f(x)在点x0处连续时,
①如果在x0附近的左侧f'(x)>0,右侧f'(x)<0,则f(x0)是极大值.
②如果在x0附近的左侧f'(x)<0,右侧f'(x)>0,则f(x0)是极小值.
提醒(1)可导函数在极值点处的导数为0,但导数为0的点不一定是极值点,如函数f(x)=x3,x=0就不是极值点,但f'(0)=0.
(2)极值点不是一个点,而是一个数x0,当x=x0时,函数取得极值.在x0处有f'(x0)=0是函数f(x)在x0处取得极值的必要不充分条件.
(3)函数f(x)在一闭区间上的最大值是此函数在此区间上的极大值与其端点函数值中的最大值,函数f(x)在一闭区间上的最小值是此函数在此区间上的极小值与其端点函数值中的最小值.
(2)极值与最值的区别与联系
①区别:
函数的极值 函数的最值
函数的极值点一定出现在区间的内部,区间的端点不能成为极值点 使函数取得最大值,最小值的点可能在区间的内部,也可能在区间的端点
函数的极值是通过比较极值点附近的函数值得出的 函数的最值是通过比较整个定义域内的函数值得出的
函数的极值可能不止一个,也可能一个没有 函数在其定义区间上的最大值、最小值最多各有一个
函数的极大值不一定大于函数的极小值 函数的最大值一定大于函数的最小值
②联系:(ⅰ)当连续函数在开区间内的极值点只有一个时,相应的极值点必为函数的最值点;
(ⅱ)极值有可能是最值,但最值只要不在区间端点处取得,其必定是极值.
13.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
14.三角函数的诱导公式
公式一:
sin(2kπ+α)=sin α,cos(2kπ+α)=cos α,tan(2kπ+α)=tan α,k∈Z.
公式二:
sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.
公式三:
sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.
公式四:
sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.
公式五:
提醒奇变偶不变,符号看象限
“奇、偶”指的是 的倍数是奇数还是偶数.“变与不变”指的是三角函数名称的变化,“变”是指正弦变余弦(或余弦变正弦).“符号看象限”的含义是:把角α看作锐角,看n· ±α(n∈Z)是第几象限角,从而得到等式右边是正号还是负号.
15.三角函数的图象变换
(1)y=sin x的图象向左平移φ(φ>0)个单位长度得到y=sin(x+φ)的图象(当φ<0时,则向右平移|φ|个单位长度).
(2)y=sin x的图象上所有点的纵坐标保持不变,横坐标变为原来的 倍,得到y=sin ωx的图象.
(3)y=sin x的图象上所有点的横坐标保持不变,纵坐标变为原来的A倍,得到y=Asin x的图象.
提醒(1)由y=sin ωx的图象经过平移变换得到y=sin(ωx+φ)的图象,平移的单
(2)函数图象平移、伸缩变换的实质是点的变化,所以可以借助三角函数图象上特征点坐标的变化寻找平移、伸缩变换的规律,一般借助于两个函数图象上的最高点或最低点的坐标来分析.
16.三角函数的对称性
(4)求曲线y=Asin(ωx+φ)(或y=Acos(ωx+φ),y=Atan(ωx+φ))的对称中心(或对称轴),只需令ωx+φ等于对应的值,求出x即可.
17.三角恒等变换
(1)两角和与差的正弦、余弦、正切公式
sin(α±β)=sin αcos β±cos αsin β.
cos(α±β)=cos αcos β sin αsin β.
(2)二倍角公式
sin 2α=2sin αcos α.
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
18.正弦定理、余弦定理及其推论
(1)正弦定理
b=2Rsin B,c=2Rsin C a∶b∶c=sin A∶sin B∶sin C.
(2)余弦定理
a2=b2+c2-2bccos A,b2=c2+a2-2cacos B,c2=a2+b2-2abcos C.
(3)三角形内角和定理
(4)三角形面积公式
19.平面向量
(1)平面向量共线的坐标表示的两种形式
①若a=(x1,y1),b=(x2,y2),则a∥b x1y2=x2y1,此形式对任意向量a,b(b≠0)都适用.
(2)有关数量积应用的常见结论
已知非零向量a=(x1,y1),b=(x2,y2),则:
①a⊥b a·b=0 x1x2+y1y2=0.
20.等差数列
(1)等差数列的判断方法
①定义法:an+1-an=d(d为常数,n∈N*) {an}是等差数列.
②通项公式法:an=a1+(n-1)d(其中a1,d为常数,n∈N*) {an}为等差数列.
③等差中项法:2an+1=an+an+2(n∈N*) {an}是等差数列.
④前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列.
(2)等差数列前n项和的最大值、最小值的求法
①通项公式法:当a1>0,d<0时,Sn有最大值,可由an≥0且an+1≤0求得n,从而求出Sn的最大值;当a1<0,d>0时,Sn有最小值,可由an≤0且an+1≥0求得n,从而求出Sn的最小值.
②二次函数法:用求二次函数最值的方法求Sn的最值.
值得注意的是n∈N*,因此等差数列前n项和取得最值时n的值可能不是一个值,也有可能是两个值.
21.等比数列的判断方法
(3)通项公式法:an=a1qn-1(其中a1,q为非零常数,n∈N*) {an}为等比数列.
提醒判断一个数列是否是等比数列,还有一种直观的判断方法,即前n项和公式法:若Sn表示数列{an}的前n项和,且Sn=-aqn+a(a≠0,q≠0,q≠1),则数列{an}是公比为q的等比数列.但此方法不能用于证明一个数列是等比数列.
22.数列中项的最值的求法
(1)根据数列与函数之间的对应关系,构造相应的函数f(n)=an,利用求解函数最值的方法(多利用函数的单调性)进行求解,但要注意自变量的取值必须是正整数的限制.
(2)利用数列的单调性求解,由不等式an+1≥an(或an+1≤an)求解出n的取值范围,从而确定数列单调性的变化,进而确定相应的最值.
(3)转化为关于n的不等式组求解:若求数列{an}的最大项,则可解不等式组
23.不等式的解法
(1)分式不等式的解法
提醒对于解分式不等式,将分式不等式转化成整式不等式时,如果不等式是含有等号的不等式形式,则很容易忘掉分母不为0的情形,从而导致出错;另一种可能出现错误的情形是在将两边进行平方时,容易扩大或缩小不等式的范围.
(2)指数、对数不等式的解法
①解指数、对数不等式的依据是指数、对数函数的概念和性质,因而同底法是解指数、对数不等式的基本方法.当然最终的目的是将它们转化为代数不等式,其主要类型和解法有:
(ⅰ)af(x)>aφ(x) f(x)>φ(x)(a>1)或f(x)<φ(x)(0
(3)一元二次不等式的恒成立问题
①在实数集R上,ax2+bx+c>0(<0)恒成立,则a>0(a<0),且Δ<0,反之也成立;ax2+bx+c≥0(≤0)恒成立,则a>0(a<0),且Δ≤0,反之也成立.
②若一元二次不等式在某一区间上恒成立,则可结合相应二次函数的图象,判断函数图象在这个区间上与对称轴的相对位置,列出不等式恒成立时满足的条件即可.
③一般地,不等式恒成立问题通常转化为函数的最值问题来解决.如f(x)≤a恒成立 f(x)max≤a,f(x)≥a恒成立 f(x)min≥a.
24.基本不等式
(1)基本不等式的变形
①根式形式:a+b≥2 (a>0,b>0),当且仅当a=b时,等号成立.
(2)利用基本不等式求最值
提醒利用基本不等式求最大值、最小值时应注意“一正、二定、三相等”,即:①所求式中的相关项必须是正数;②求积xy的最大值时,要看和x+y是否为定值.求和x+y的最小值时,要看积xy是否为定值.求解时,常用到“拆项”“凑项”等解题技巧;③当且仅当各项相等时,才能取等号.以上三点应特别注意,缺一不可.
25.空间几何体的表面积和体积
(1)直棱柱的侧面积:S侧=cl(c是底面周长,l为侧棱长).
(2)柱体的体积:V柱=Sh(S为底面积,h是柱体的高).
26.球的组合体
(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长,正方体的棱切球的直径是正方体的面对角线长,正方体的外接球的直径是正方体的体对角线长.
27.证明空间位置关系的方法
提醒利用定理证明线面关系时要注意结合几何体的结构特征,尤其要注意灵活利用正棱柱、正棱锥等特殊几何体的性质,进行空间线面关系的相互转化.
28.空间向量的坐标运算
设a=(a1,a2,a3),b=(b1,b2,b3),则
(1)a·b=a1b1+a2b2+a3b3;
(2)a∥b a1=λb1,a2=λb2,a3=λb3(λ∈R,b≠0);
(3)a⊥b a1b1+a2b2+a3b3=0(b≠0);
29.空间向量的应用
(1)夹角公式:设非零向量a=(a1,a2,a3),b=(b1,b2,b3),则
提醒在处理实际问题时,要根据具体图形确定二面角的平面角是锐角还是钝角,以确定角的大小.
30.直线
(1)直线方程的5种形式
名称 方程的形式 常数的几何意义 适用范围
点斜式 y-y0=k(x-x0) (x0,y0)是直线上一定点,k是斜率 不垂直于x轴
斜截式 y=kx+b k是斜率,b是直线在y轴上的截距 不垂直于x轴
(2)两条直线的位置关系
①已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1,B1,A2,B2全不为0),则l1,l2
当A1,B1,A2,B2中有0时,应单独讨论.
②直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0垂直 A1A2+B1B2=0.
提醒讨论两条直线的位置关系时应注意斜率不存在或斜率为0的情况,当两条直线中一条直线的斜率不存在,另一条直线的斜率为0时,它们也垂直.
31.圆
(1)圆的四种方程
①圆的标准方程:(x-a)2+(y-b)2=r2(r>0).
②圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
④圆的直径式方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0(圆的直径的端点是A(x1,y1),B(x2,y2)).
(2)直线与圆的位置关系
直线l:Ax+By+C=0和圆C:(x-a)2+(y-b)2=r2(r>0)有相交、相离、相切三种情况.可从代数和几何两个方面来判断:
①代数方法(判断直线与圆的方程联立所得方程组的解的情况):Δ>0 相交;Δ<0 相离;Δ=0 相切;
②几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为d,则d
(3)圆与圆的位置关系
位置关系 几何法 代数法 公切线的条数
圆心距d与r1,r2的关系 联立两圆方程组成方程组的解的情况
外离 d>r1+r2 无解 4
外切 d=r1+r2 一组实数解 3
相交 |r1-r2|
内含 0≤d<|r1-r2|(r1≠r2) 无解 0
32.椭圆
标准方程
几 何 性 质 范围 -a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a
对称性 对称轴:x轴,y轴;对称中心:原点
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
顶点 A1(-a,0),A2(a,0); B1(0,-b),B2(0,b) A1(0,-a),A2(0,a);
B1(-b,0),B2(b,0)
轴 线段A1A2,B1B2分别是椭圆的长轴和短轴,长轴长为2a,短轴长为2b
焦距 |F1F2|=2c
离心率 焦距与长轴长的比值:e∈(0,1)
a,b,c的关系 b2=a2-c2
33.双曲线
(1)双曲线的标准方程及几何性质
几 何 性 质 范围 |x|≥a,y∈R |y|≥a,x∈R
对称性 对称轴:x轴,y轴;对称中心:原点
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为2a,虚轴长为2b
焦距 |F1F2|=2c
离心率 焦距与实轴长的比值:e∈(1,+∞)
渐近线
a,b,c的关系 b2=c2-a2
提醒①离心率e的取值范围是(1,+∞).当e越接近于1时,双曲线开口越小;当e越接近于+∞时,双曲线开口越大.
②满足||PF1|-|PF2||=2a的点P的轨迹不一定是双曲线,当2a=0时,点P的轨迹是线段F1F2的中垂线;当0<2a<|F1F2|时,点P的轨迹是双曲线;当2a=|F1F2|时,点P的轨迹是两条射线;当2a>|F1F2|时,点P的轨迹不存在.
(2)双曲线方程与渐近线方程的关系
34.抛物线
(1)抛物线的标准方程及几何性质
(2)抛物线焦点弦的常用结论
设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),α为直线AB的倾斜角,则
35.直线与圆锥曲线的位置关系
(1)弦长的求解方法
设直线与圆锥曲线交于A(x1,y1),B(x2,y2)两点,若直线AB的斜率存在(设为k),
当直线AB的斜率不存在时,可直接求出直线与圆锥曲线的交点坐标,利用两点间的距离公式求弦长.
(2)圆锥曲线中的最值问题
①利用圆锥曲线的定义进行转化,一般在三点共线时取得最值.
②求圆锥曲线上的点到已知直线的距离的最值,当已知直线的平行线与圆锥曲线相切时,两平行线间的距离即为所求.
③利用基本不等式求最值.
36.频率与概率的区别与联系
(1)区别
①频率具有随机性,在不同的试验中,同一事件发生的频率可能不同;
②概率是频率的稳定值,是一个确定的常数,不管进行多少次试验,同一事件发生的概率是不变的.
(2)联系
①频率和概率都是用来刻画随机事件发生的可能性大小的量;
②概率可看作频率在理论上的期望值,随试验次数的增加,频率可近似地作为这个事件的概率.
37.事件的关系与运算
(1)包含关系:如果事件A发生,则事件B一定发生,这时称事件B包含事件A,记作B A(或A B).
(2)相等事件:如果B A且A B,那么称事件A与事件B相等,记作A=B.
(3)并(和)事件:若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).
(4)交(积)事件:若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件),记作A∩B(或AB).
(5)互斥事件:若A∩B为不可能事件(即A∩B= ),那么称事件A与事件B互斥,其含义是事件A与事件B在任何一次试验中都不会同时发生.
(6)对立事件:若A∩B为不可能事件,A∪B为必然事件,那么称事件A与事件B互为对立事件,其含义是事件A与事件B在任何一次试验中有且只有一个发生.
提醒互斥事件与对立事件都是指两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生以外,还要求二者必须有一个发生.因此,对立事件一定是互斥事件,而互斥事件未必是对立事件.
38.概率的几个基本性质
(1)任何事件A的概率都在0~1之间,即0≤P(A)≤1.
(2)若A B,则P(A)≤P(B).
(3)必然事件发生的概率为1,不可能事件发生的概率为0.
(4)当事件A与事件B互斥时,P(A+B)=P(A)+P(B).注意没有事件A与事件B互斥这一条件时,这个公式不成立.
(5)若事件A与事件B互为对立事件,则P(A)+P(B)=1.
提醒当一事件的概率不易直接求,但其对立事件的概率易求时,可运用(5),即用间接法求概率.
39.古典概型的概率公式
如果随机事件A包含的基本事件数为m,总的基本事件数为n,则
提醒求解古典概型问题的步骤
(1)判断本次试验的结果是否是等可能的,设出所求的事件A.
(2)分别计算总的基本事件的个数n和所求的事件A所包含的基本事件的个数m.
40.均值的相关结论
(1)E(k)=k(k为常数).
(2)E(aX+b)=aE(X)+b.
(3)E(X1+X2)=E(X1)+E(X2).
(4)若X1,X2相互独立,则E(X1·X2)=E(X1)·E(X2).
(5)若随机变量X服从两点分布,则E(X)=p.
(6)若X服从二项公布,即X~B(n,p),则E(X)=np.
提醒E(X)是一个常数,由X的分布列唯一确定,它描述X取值的平均状态,作为随机变量X是可变的,可取不同的值.
41.方差的相关性质结论
(1)D(k)=0(k为常数).
(2)D(aX+b)=a2D(X).
(3)D(X)=E(X2)-[E(X)]2.
(4)若X1,X2,…,Xn两两独立,则D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn).
提醒①随机变量的方差与标准差都反映了随机变量取值的稳定与波动,集中与离散程度,其中标准差与随机变量本身有相同的单位.
②方差也是一个常数,它不具有随机性,方差的值一定是非负的.
42.二项分布与正态分布
②正态分布密度函数的性质:函数图象关于直线x=μ对称;σ(σ>0)的大小决定函数图象的“胖”“瘦”;P(μ-σ
43.排列数、组合数公式及其相关性质
(1)排列数
①公式
(2)组合数
①公式
44.求解排列组合问题常用的解题方法
(1)元素相邻的排列问题——“捆绑”法.
(2)元素相间的排列问题——“插空”法.
(3)元素有顺序限制的排列问题——“除序”法,即先把这几个有顺序限制的元素及其他元素一同进行全排列,然后用总的排列数除以这几个元素的全排列数.
(4)带有“含”“不含”“至多”“至少”的组合(排列)问题——间接法,即先不考虑限制条件求出组合(排列)数,再排除不符合要求的组合(排列)数.
45.二项式定理
(2)二项式系数与项的系数是两个完全不同的概念,二项式系数与a,b的值无关,项的系数不仅与项数有关,也与a,b的值有关.
46.两种抽样法
类别 共同点 各自特点 联系 适用范围
简单随 机抽样 ①抽样过程中每个个体被抽到的可能性相等; ②每次抽出个体后不再将它放回,即不放回抽样 从总体中逐个抽取 最基本的抽样方法 总体中的个体较少
分层 抽样 将总体分成几层,分层按比例进行抽取 分层抽样时采用简单随机抽样或系统抽样 总体由差异明显的几部分组成
提醒用分层抽样法抽样时,各层抽样标准要一致,互不重叠;各层抽取的比例都等于样本容量在总体中的比例,即为
47.变量间的相关关系
线性相关系数r是从数值上来判断变量间的线性相关程度的,|r|的值越接近于1,说明变量之间的线性相关程度越高;|r|的值越接近于0,说明变量之间的线性相关程度越低.当两个变量的关系可用一次函数表示时,r=±1,若斜率为正,r=1,否则r=-1.r为正时表示正相关,r为负时表示负相关.
48.线性回归方程的求解步骤
(1)利用散点图或进行相关性检验判定两个变量具有线性相关关系.
(4)写出线性回归方程.
提醒回归直线一定经过样本点的中心( ),据此性质可以解决有关的计算问题、判断结论的正确性.
49.独立性检验的基本方法
一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表如表:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
根据观测数据计算由公式K2= 所给出的随机变量K2的观测值k,并且k的值越大,说明“X与Y有关系”成立的可能性越大,可以利用数据来确定“X和Y有关系”的可信程度.
50.复数的四则运算法则
(1)(a+bi)±(c+di)=(a±c)+(b±d)i.
(2)(a+bi)(c+di)=(ac-bd)+(bc+ad)i.
提醒几个结论:①(1±i)2=±2i.
同课章节目录
