专题四 4.2.2 求数列的通项及前n项和 课件(共52张PPT)
文档属性
| 名称 | 专题四 4.2.2 求数列的通项及前n项和 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:54:59 | ||
图片预览





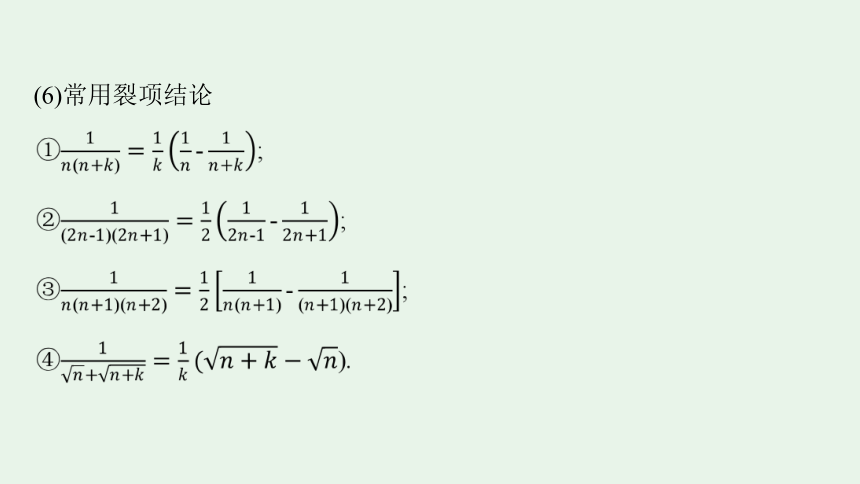






文档简介
(共52张PPT)
4.2.2 求数列的通项及前n项和
第三部分
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
03
核心素养微专题(五)
必备知识 精要梳理
1.由递推关系式求数列的通项公式
(1)形如an+1=an+f(n),利用累加法求通项.
(2)形如an+1=anf(n),利用累乘法求通项.
(3)形如an+1=pan+q,等式两边同时加 转化为等比数列求通项.
2.数列求和的常用方法
(1)公式法:利用等差数列、等比数列的求和公式.
(2)错位相减法:适合求数列{an·bn}的前n项和Sn,其中{an},{bn}一个是等差数列,另一个是等比数列.
(3)裂项相消法:将数列的通项分成两个式子的代数和,通过累加抵消中间若干项的方法.
(4)拆项分组法:先把数列的每一项拆成两项(或多项),再重新组合成两个(或多个)简单的数列,最后分别求和.
(5)并项求和法:把数列的两项(或多项)组合在一起,重新构成一个数列再求和,适用于正负相间排列的数列求和.
(6)常用裂项结论
关键能力 学案突破
热点一
求通项及错位相减法求和
【例1】(2020山东潍坊一模,18)在①b2n=2bn+1,②a2=b1+b2,③b1,b2,b4成等比数列这三个条件中选择符合题意的两个条件,补充在下面的问题中,并求解.
已知数列{an}中a1=1,an+1=3an,公差不等于0的等差数列{bn}满足 ,求数列 的前n项和Sn.
解 因a1=1,an+1=3an,所以数列{an}是以1为首项,公比为3的等比数列,所以an=3n-1.
选①②时,设数列{bn}公差为d,
因为a2=3,所以b1+b2=3.
因为b2n=2bn+1,所以n=1时,b2=2b1+1,
选②③时,设数列{bn}公差为d,因为a2=3,所以b1+b2=3,即2b1+d=3.
因为b1,b2,b4成等比数列,所以 =b1b4,即(b1+d)2=b1(b1+3d),
化简得d2=b1d,因为d≠0,所以b1=d,从而d=b1=1,所以bn=n.
选①③时,设数列{bn}公差为d,因为b2n=2bn+1,所以n=1时,b2=2b1+1,所以d=b1+1.
又因为b1,b2,b4成等比数列,所以 =b1b4,即(b1+d)2=b1(b1+3d),化简得d2=b1d,因为d≠0,所以b1=d,从而无解,所以等差数列{bn}不存在,故不合题意.
解题心得若已知数列为等差或等比数列,求其通项是利用等差、等比数列通项公式,或通过变形转换成等差、等比数列求通项;如果数列{an}与数列{bn}分别是等差数列和等比数列,那么数列{an·bn}的前n项和采用错位相减法来求.
【对点训练1】(2020全国Ⅰ,理17)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
解 (1)设{an}的公比为q,由题设得2a1=a2+a3,即2a1=a1q+a1q2.
所以q2+q-2=0,解得q=1(舍去),q=-2.故{an}的公比为-2.
(2)记Sn为{nan}的前n项和.
由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n
热点二
求通项及裂项相消法求和
【例2】(2020山东潍坊二模,18)已知数列{an}为正项等比数列,a1=1,数列{bn}满足b2=3,a1b1+a2b2+a3b3+…+anbn=3+(2n-3)2n.
(1)求an;
解 (1)令n=1,得a1b1=3+(2-3)×2=1,所以b1=1.
令n=2,得a1b1+a2b2=7,
所以a2b2=6.又因为b2=3,所以a2=2.设数列{an}的公比为q,则q= =2,所以an=2n-1.
(2)当n≥2时,a1b1+a2b2+…+an-1bn-1=3+(2n-5)2n-1,①
又a1b1+a2b2+a3b3+…+anbn=3+(2n-3)2n,②
②-①得anbn=3+(2n-3)2n-[3+(2n-5)2n-1]=(2n-1)2n-1,
得bn=2n-1,n=1时也成立,
解题心得1.若条件等式中含有an,Sn的关系式,或已知条件中含有数列通项的较为复杂的关系式,条件转化的常用方法是由已知关系式再推出一个关系式相减.
2.把数列的通项拆成两项之差,求和时中间的项能够抵消,从而求得其和.注意抵消后所剩余的项一般前后对称.
【对点训练2】(2020浙江,20)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1-an,cn+1= ·cn,n∈N*.
(1)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(2)若{bn}为等差数列,公差d>0,证明:c1+c2+…+cn<1+ ,n∈N*.
热点三
求通项及分组求和或并项求和
【例3】(2020山西大同模拟五,17)已知数列{an}满足a1=1,
nan+1-2(n+1)an=n2+n(n∈N*).
(1)求证:数列 为等比数列;
(2)求数列{an}的前n项和Sn.
解题心得1.若能把一个较为复杂的数列的通项分成两(或多)部分,而每一部分对应的前n项的和可求,则分别求和相加即可.
2.若一个数列的前n项和不好求,而数列相邻的两项或多项的和相等且为常数,则对该数列先作并项处理,即先合并项,再求和.
【对点训练3】(2020河南安阳二模,理17)记数列{an}的前n项和为Sn,已知Sn=2an-2n+1.
(1)求数列{an}的通项公式;
解 (1)当n=1时,由Sn=2an-2n+1,可得a1=S1=2a1-2+1,解得a1=1.
当n≥2时,an=Sn-Sn-1=2an-2n+1-2an-1+2(n-1)-1,即为an=2an-1+2,可得an+2=2(an-1+2),显然an-1+2≠0,则 =2.
所以数列{an+2}是首项为3,公比为2的等比数列,则an+2=3·2n-1,
即an=3·2n-1-2.
热点四
数列中的存在性问题
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ~3”数列,且an≥0 若存在,求λ的取值范围;若不存在,说明理由.
解 (1)因为等差数列{an}是“λ~1”数列,则Sn+1-Sn=λan+1,即an+1=λan+1,
也即(λ-1)an+1=0,此式对一切正整数n均成立.
若λ≠1,则an+1=0恒成立,故a3-a2=0,而a2-a1=-1,
这与{an}是等差数列矛盾.
所以λ=1.(此时,任意首项为1的等差数列都是“1~1”数列)
①若λ≤0或λ=1,则(*)只有一解为cn=1,即符合条件的数列{an}只有一个.(此数列为1,0,0,0,…)
即符合条件的数列{an}只有一个.(此数列为1,0,0,0,…)
则方程(*)有两个大于或等于1的解:其中一个为1,另一个大于1(记此解为t).
所以Sn+1=Sn或Sn+1=t3Sn.
由于数列{Sn}从任何一项求其后一项均有两种不同结果,所以这样的数列{Sn}有无数多个,则对应的{an}有无数多个.
综上所述,能存在三个各项非负的数列{an}为“λ~3”数列,λ的取值范围是(0,1).
解题心得解决数列中的存在性问题的一般方法是假设推理法.即先假设所探求对象存在或结论成立,以此假设为前提条件进行运算或逻辑推理,若由此推出矛盾,则假设不成立,即不存在.若推不出矛盾,即得到存在的结果.
【对点训练4】(2020天津河西区校级联考,17)设各项均为正数的等比数列{an}(n∈N*)中,a1+a3=10,a3+a5=40.设bn=log2an.
(1)求数列{bn}的通项公式;
(1)解 设各项均为正数的等比数列{an}的公比为q,
则a1+a1q2=10,a1q2+a1q4=40,
解得a1=2,q=2,即有an=2n,bn=log22n=n.
核心素养微专题(五)
求解数列与多模块知识综合题
答案 B
到该直线的距离的两倍.
点Cn到直线距离的最大值为圆心到直线的距离与圆的半径之和,
核心素养分析本题是数学多模块知识的综合题,对核心素养要求较高.先用“数学抽象”将 转化为∠AnOBn=120°;其次运用“直观想象”将两点到直线的距离之和转化为一点到直线的距离;再运用“逻辑推理”将距离的最大值转化为圆心到直线的距离与圆的半径之和;最后运用“数列运算”求出数列的和及得出结果.
A.250+2 449 B.250+2 549
C.249+2 449 D.249+2 549
答案 C
∴x=2为f(x)的第一个极大值点.
又当3∵函数不能在端点处取得极值,
∴an=2n,1≤n≤49,n∈N*,∴对应极大值bn=2n-1,1≤n≤49,n∈N*.
A.-4 B.-2 C.0 D.2
答案 AB
∴-2t2-(a+1)t+a2-a+2≥2对于任意的t∈[1,2]恒成立,
整理得[2t-(a-1)](t+a)≤0对于任意的t∈[1,2]恒成立,
对A,由a=-4,得出t∈[1,2]不等式(2t+5)(t-4)≤0恒成立,故A正确;
对B,由a=-2,得出t∈[1,2]不等式(2t+3)(t-2)≤0恒成立,故B正确;
对C,由a=0,得出t∈[1,2]不等式(2t+1)t≤0不恒成立,故C错误;
对D,由a=2,得出t∈[1,2]不等式(2t-1)(t+2)≤0不恒成立,故D错误,故选AB.
【跟踪训练2】(2020山东潍坊一模,16)定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,例如[1.3]=1,[-1.5]=-2,[2]=2,当x∈[0,n)(n∈N*)时,f(x)的值域为An.记集合An中元素的个数为an,则 的值为 .
解析 根据题意,[x]表示不超过x的最大整数,
4.2.2 求数列的通项及前n项和
第三部分
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
03
核心素养微专题(五)
必备知识 精要梳理
1.由递推关系式求数列的通项公式
(1)形如an+1=an+f(n),利用累加法求通项.
(2)形如an+1=anf(n),利用累乘法求通项.
(3)形如an+1=pan+q,等式两边同时加 转化为等比数列求通项.
2.数列求和的常用方法
(1)公式法:利用等差数列、等比数列的求和公式.
(2)错位相减法:适合求数列{an·bn}的前n项和Sn,其中{an},{bn}一个是等差数列,另一个是等比数列.
(3)裂项相消法:将数列的通项分成两个式子的代数和,通过累加抵消中间若干项的方法.
(4)拆项分组法:先把数列的每一项拆成两项(或多项),再重新组合成两个(或多个)简单的数列,最后分别求和.
(5)并项求和法:把数列的两项(或多项)组合在一起,重新构成一个数列再求和,适用于正负相间排列的数列求和.
(6)常用裂项结论
关键能力 学案突破
热点一
求通项及错位相减法求和
【例1】(2020山东潍坊一模,18)在①b2n=2bn+1,②a2=b1+b2,③b1,b2,b4成等比数列这三个条件中选择符合题意的两个条件,补充在下面的问题中,并求解.
已知数列{an}中a1=1,an+1=3an,公差不等于0的等差数列{bn}满足 ,求数列 的前n项和Sn.
解 因a1=1,an+1=3an,所以数列{an}是以1为首项,公比为3的等比数列,所以an=3n-1.
选①②时,设数列{bn}公差为d,
因为a2=3,所以b1+b2=3.
因为b2n=2bn+1,所以n=1时,b2=2b1+1,
选②③时,设数列{bn}公差为d,因为a2=3,所以b1+b2=3,即2b1+d=3.
因为b1,b2,b4成等比数列,所以 =b1b4,即(b1+d)2=b1(b1+3d),
化简得d2=b1d,因为d≠0,所以b1=d,从而d=b1=1,所以bn=n.
选①③时,设数列{bn}公差为d,因为b2n=2bn+1,所以n=1时,b2=2b1+1,所以d=b1+1.
又因为b1,b2,b4成等比数列,所以 =b1b4,即(b1+d)2=b1(b1+3d),化简得d2=b1d,因为d≠0,所以b1=d,从而无解,所以等差数列{bn}不存在,故不合题意.
解题心得若已知数列为等差或等比数列,求其通项是利用等差、等比数列通项公式,或通过变形转换成等差、等比数列求通项;如果数列{an}与数列{bn}分别是等差数列和等比数列,那么数列{an·bn}的前n项和采用错位相减法来求.
【对点训练1】(2020全国Ⅰ,理17)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
解 (1)设{an}的公比为q,由题设得2a1=a2+a3,即2a1=a1q+a1q2.
所以q2+q-2=0,解得q=1(舍去),q=-2.故{an}的公比为-2.
(2)记Sn为{nan}的前n项和.
由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n
热点二
求通项及裂项相消法求和
【例2】(2020山东潍坊二模,18)已知数列{an}为正项等比数列,a1=1,数列{bn}满足b2=3,a1b1+a2b2+a3b3+…+anbn=3+(2n-3)2n.
(1)求an;
解 (1)令n=1,得a1b1=3+(2-3)×2=1,所以b1=1.
令n=2,得a1b1+a2b2=7,
所以a2b2=6.又因为b2=3,所以a2=2.设数列{an}的公比为q,则q= =2,所以an=2n-1.
(2)当n≥2时,a1b1+a2b2+…+an-1bn-1=3+(2n-5)2n-1,①
又a1b1+a2b2+a3b3+…+anbn=3+(2n-3)2n,②
②-①得anbn=3+(2n-3)2n-[3+(2n-5)2n-1]=(2n-1)2n-1,
得bn=2n-1,n=1时也成立,
解题心得1.若条件等式中含有an,Sn的关系式,或已知条件中含有数列通项的较为复杂的关系式,条件转化的常用方法是由已知关系式再推出一个关系式相减.
2.把数列的通项拆成两项之差,求和时中间的项能够抵消,从而求得其和.注意抵消后所剩余的项一般前后对称.
【对点训练2】(2020浙江,20)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1-an,cn+1= ·cn,n∈N*.
(1)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(2)若{bn}为等差数列,公差d>0,证明:c1+c2+…+cn<1+ ,n∈N*.
热点三
求通项及分组求和或并项求和
【例3】(2020山西大同模拟五,17)已知数列{an}满足a1=1,
nan+1-2(n+1)an=n2+n(n∈N*).
(1)求证:数列 为等比数列;
(2)求数列{an}的前n项和Sn.
解题心得1.若能把一个较为复杂的数列的通项分成两(或多)部分,而每一部分对应的前n项的和可求,则分别求和相加即可.
2.若一个数列的前n项和不好求,而数列相邻的两项或多项的和相等且为常数,则对该数列先作并项处理,即先合并项,再求和.
【对点训练3】(2020河南安阳二模,理17)记数列{an}的前n项和为Sn,已知Sn=2an-2n+1.
(1)求数列{an}的通项公式;
解 (1)当n=1时,由Sn=2an-2n+1,可得a1=S1=2a1-2+1,解得a1=1.
当n≥2时,an=Sn-Sn-1=2an-2n+1-2an-1+2(n-1)-1,即为an=2an-1+2,可得an+2=2(an-1+2),显然an-1+2≠0,则 =2.
所以数列{an+2}是首项为3,公比为2的等比数列,则an+2=3·2n-1,
即an=3·2n-1-2.
热点四
数列中的存在性问题
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ~3”数列,且an≥0 若存在,求λ的取值范围;若不存在,说明理由.
解 (1)因为等差数列{an}是“λ~1”数列,则Sn+1-Sn=λan+1,即an+1=λan+1,
也即(λ-1)an+1=0,此式对一切正整数n均成立.
若λ≠1,则an+1=0恒成立,故a3-a2=0,而a2-a1=-1,
这与{an}是等差数列矛盾.
所以λ=1.(此时,任意首项为1的等差数列都是“1~1”数列)
①若λ≤0或λ=1,则(*)只有一解为cn=1,即符合条件的数列{an}只有一个.(此数列为1,0,0,0,…)
即符合条件的数列{an}只有一个.(此数列为1,0,0,0,…)
则方程(*)有两个大于或等于1的解:其中一个为1,另一个大于1(记此解为t).
所以Sn+1=Sn或Sn+1=t3Sn.
由于数列{Sn}从任何一项求其后一项均有两种不同结果,所以这样的数列{Sn}有无数多个,则对应的{an}有无数多个.
综上所述,能存在三个各项非负的数列{an}为“λ~3”数列,λ的取值范围是(0,1).
解题心得解决数列中的存在性问题的一般方法是假设推理法.即先假设所探求对象存在或结论成立,以此假设为前提条件进行运算或逻辑推理,若由此推出矛盾,则假设不成立,即不存在.若推不出矛盾,即得到存在的结果.
【对点训练4】(2020天津河西区校级联考,17)设各项均为正数的等比数列{an}(n∈N*)中,a1+a3=10,a3+a5=40.设bn=log2an.
(1)求数列{bn}的通项公式;
(1)解 设各项均为正数的等比数列{an}的公比为q,
则a1+a1q2=10,a1q2+a1q4=40,
解得a1=2,q=2,即有an=2n,bn=log22n=n.
核心素养微专题(五)
求解数列与多模块知识综合题
答案 B
到该直线的距离的两倍.
点Cn到直线距离的最大值为圆心到直线的距离与圆的半径之和,
核心素养分析本题是数学多模块知识的综合题,对核心素养要求较高.先用“数学抽象”将 转化为∠AnOBn=120°;其次运用“直观想象”将两点到直线的距离之和转化为一点到直线的距离;再运用“逻辑推理”将距离的最大值转化为圆心到直线的距离与圆的半径之和;最后运用“数列运算”求出数列的和及得出结果.
A.250+2 449 B.250+2 549
C.249+2 449 D.249+2 549
答案 C
∴x=2为f(x)的第一个极大值点.
又当3
∴an=2n,1≤n≤49,n∈N*,∴对应极大值bn=2n-1,1≤n≤49,n∈N*.
A.-4 B.-2 C.0 D.2
答案 AB
∴-2t2-(a+1)t+a2-a+2≥2对于任意的t∈[1,2]恒成立,
整理得[2t-(a-1)](t+a)≤0对于任意的t∈[1,2]恒成立,
对A,由a=-4,得出t∈[1,2]不等式(2t+5)(t-4)≤0恒成立,故A正确;
对B,由a=-2,得出t∈[1,2]不等式(2t+3)(t-2)≤0恒成立,故B正确;
对C,由a=0,得出t∈[1,2]不等式(2t+1)t≤0不恒成立,故C错误;
对D,由a=2,得出t∈[1,2]不等式(2t-1)(t+2)≤0不恒成立,故D错误,故选AB.
【跟踪训练2】(2020山东潍坊一模,16)定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,例如[1.3]=1,[-1.5]=-2,[2]=2,当x∈[0,n)(n∈N*)时,f(x)的值域为An.记集合An中元素的个数为an,则 的值为 .
解析 根据题意,[x]表示不超过x的最大整数,
同课章节目录
