专题六 6.1 排列、组合、二项式定理小题组合练 课件(共30张PPT)
文档属性
| 名称 | 专题六 6.1 排列、组合、二项式定理小题组合练 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 01:02:17 | ||
图片预览











文档简介
(共30张PPT)
6.1 排列、组合、二项式定理小题组合练
第三部分
考 情 分 析 计数原理和统计与概率是高中阶段数学的重要内容,也是高考中非常重要的内容,因其与现实生活联系密切,所以成为高考命制应用题的主要来源,高考出题频率基本是“两小一大”,排列组合应用题、二项式定理、抽样方法、样本估计总体、相互独立事件、独立重复试验、条件概率、数字特征等,都可能在小题中考查,难度一般不大.
统计与概率解答题是高考六道解答题必考题之一,一般以现实生活中的真实情境为背景,考查回归分析、独立性检验、离散型随机变量的分布列、期望、方差等,常与统计图表结合,题目阅读量较大,与实际生活等联系密切,难度中等.偶尔也可能会与函数、数列、导数等知识综合命题.
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.两个计数原理与排列组合
(1)两个计数原理
“分类”与“分步”的区别:关键是看事件完成情况,如果每种方法都能将事件完成则是分类;如果必须连续若干步才能将事件完成则是分步.分类要用分类加法计数原理将种数相加;分步要用分步乘法计数原理将种数相乘.
考向训练 限时通关
考向一
两个计数原理
1.(2020山东,3)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种 C.60种 D.30种
答案 C
2.(2020广东珠海三模,10)甲、乙、丙3人从1楼乘电梯去商场的3到9楼,每层楼最多下2人,则下电梯的方法有( )
A.210种 B.252种 C.343种 D.336种
答案 D
解析 分两种情况讨论:
①某个楼层只下1人,则3人下电梯的方法种数为 =210;②3人中有2人从一个楼层下,另1人从其他楼层选一个楼层下,此时,3人下电梯的方法种数为 =126.由分类加法计数原理可知,3人下电梯的方法种数为210+126=336.
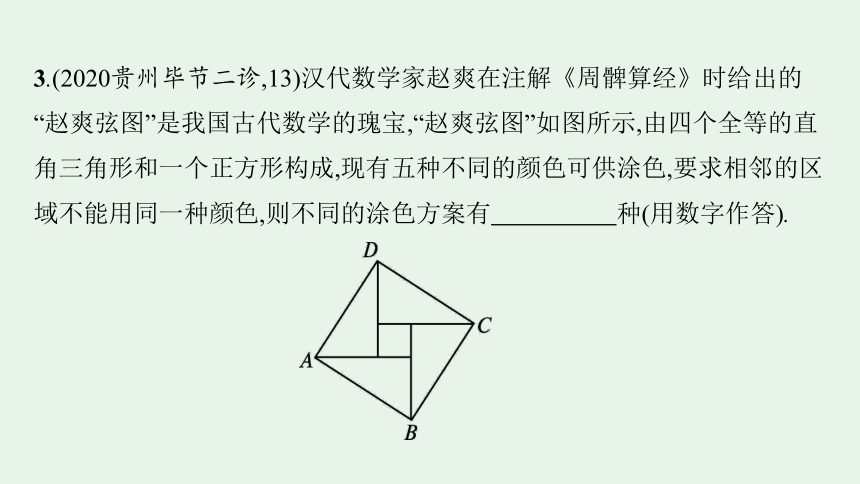
3.(2020贵州毕节二诊,13)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,“赵爽弦图”如图所示,由四个全等的直角三角形和一个正方形构成,现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有 种(用数字作答).
答案 420
解析 由题意,假设五个区域分别为①②③④⑤,对于区域①②③,三个区域两两相邻,共有 =60种涂法;
对于区域④⑤,若④与②颜色相同,则⑤有3种
涂法,若④与②颜色不同,则④有2种涂法,⑤有
2种涂法,共有2×2=4种涂法,所以④⑤共有
3+4=7种涂法,则一共有60×7=420种涂法.
4.(2020山东潍坊二模,15)植树造林,绿化祖国.某班级义务劳动志愿者小组参加植树活动,准备在一抛物线形地块上的ABCDGFE七点处各种植一棵树苗,如图所示,其中A,B,C分别与E,F,G关于抛物线的对称轴对称,现有三种树苗,要求每种树苗至少种植一棵,且关于抛物线的对称轴对称的两点处必须种植同一种树苗,则共有不同的种植方法数是 (用数字作答).
答案 36
解析 由图形的对称性,相当于3种树苗种在A,B,C,D四个位置,有且仅有一种树苗重复,所以有 =3种方法.先从A,B,C,D中任选两个位置种植同一种树苗,有 =6种方法,再把另两种树苗种植在另两个位置上,有 =2种方法.则由分步乘法计数原理知,共有3×6×2=36种方法.
5.(2020山东泰安三模,15)甲、乙、丙、丁、戊五人去参加数学、物理、化学三科竞赛,每个同学只能参加一科竞赛,若每个同学可以自由选择,则不同的选择种数是 ;若甲和乙不参加同一科,甲和丙必须参加同一科,且这三科都有人参加,则不同的选择种数是 .(用数字作答)
答案 243 30
解析 若每个同学可以自由选择,由分步乘法计数原理可得,不同的选择种数是35=243;因为甲和乙不参加同一科,甲和丙必须参加同一科,所以有2,2,1和3,1,1两种分配方案.
由分类加法计数原理,可得不同的选择种数是18+12=30.
考向二
排列组合
6.(2020山东聊城二模,4)2020年是脱贫攻坚年,为顺利完成“两不愁,三保障”,即农村贫困人口不愁吃、不愁穿,农村贫困人口义务教育、基本医疗、住房安全有保障,某市拟派出6人组成三个帮扶队,每队两人,对脱贫任务较重的甲、乙、丙三县进行帮扶,则不同的派出方法种数共有( )
A.15 B.60 C.90 D.540
答案 C
解析 依题意,首先将人平均分成3组,再将三组进行全排列即可,所以所有可能的派出方法有 =90(种).
7.(2019北京海淀一模,理8)某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A层班级,生物在B层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
第一节 第二节 第三节 第四节
地理B层2班 化学A层3班 地理A层1班 化学A层4班
生物A层1班 化学B层2班 生物B层2班 历史B层1班
物理A层1班 生物A层3班 物理A层2班 生物A层4班
物理B层2班 生物B层1班 物理B层1班 物理A层4班
政治1班 物理A层3班 政治2班 政治3班
A.8种 B.10种 C.12种 D.14种
答案 B
解析 学校课表中每一节课都有物理A层可选,政治有三节课可选,生物B层只有二、三节可选,依据关键元素优先的原则,先安排生物B的“位置”,再安排政治的“位置”,接着安排物理的“位置”,三种科目安排好后,自习课随之确定,方法数为:3×2+2×2=10.
8.(2020湖南雅礼中学高三月考,5)中国古代儒家要求学生掌握六种基本才能:礼、乐、射、御、书、数,也称这六种才能为“六艺”.某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种 B.72种
C.96种 D.144种
答案 D
9.(2020天津和平区高三一模,8)在国际高峰论坛上,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为( )
A.378 B.306 C.268 D.198
答案 D
解析 分两种情况讨论.
①若选两个国内媒体一个国外媒体,有 =90种不同提问方式;②若选两个外国媒体一个国内媒体,有 =108种不同提问方式.
所以共有90+108=198种提问方式.
10.(2020山东济宁三模,15)5人并排站成一行,如果甲乙两人不相邻,那么不同的排法种数是 .(用数字作答);5人并排站成一行,甲乙两人之间恰好有一人的概率是 .(用数字作答)
考向三
二项式定理
11.(2020海南海南中学模拟,3)已知(2x-a)6(a是常数)的展开式中含x3项的系数为-160,则a=( )
答案 A
12.(2020全国Ⅰ,理8) (x+y)5的展开式中x3y3的系数为( )
A.5 B.10 C.15 D.20
答案 C
13.(多选)(2020海南三亚模拟,10)对于 的展开式,下列说法正确的是( )
A.展开式共有6项
B.展开式中的常数项是-240
C.展开式中各项系数之和为1
D.展开式中的二项式系数之和为64
答案 CD
14.(2020山东德州二模,7)(x2-x-a)5的展开式的各项系数之和为-32,则该展开式中含x9项的系数是( )
A.-15 B.-5 C.5 D.15
答案 B
解析 ∵(x2-x-a)5的展开式的各项系数之和为-32,令x=1,可得(12-1-a)5=-32,故(-a)5=-32,得a=2.
故(x2-x-a)5=(x2-x-2)5=(x-2)5(x+1)5,设(x-2)5展开式的通项公式为
6.1 排列、组合、二项式定理小题组合练
第三部分
考 情 分 析 计数原理和统计与概率是高中阶段数学的重要内容,也是高考中非常重要的内容,因其与现实生活联系密切,所以成为高考命制应用题的主要来源,高考出题频率基本是“两小一大”,排列组合应用题、二项式定理、抽样方法、样本估计总体、相互独立事件、独立重复试验、条件概率、数字特征等,都可能在小题中考查,难度一般不大.
统计与概率解答题是高考六道解答题必考题之一,一般以现实生活中的真实情境为背景,考查回归分析、独立性检验、离散型随机变量的分布列、期望、方差等,常与统计图表结合,题目阅读量较大,与实际生活等联系密切,难度中等.偶尔也可能会与函数、数列、导数等知识综合命题.
内容索引
01
02
必备知识 精要梳理
考向训练 限时通关
必备知识 精要梳理
1.两个计数原理与排列组合
(1)两个计数原理
“分类”与“分步”的区别:关键是看事件完成情况,如果每种方法都能将事件完成则是分类;如果必须连续若干步才能将事件完成则是分步.分类要用分类加法计数原理将种数相加;分步要用分步乘法计数原理将种数相乘.
考向训练 限时通关
考向一
两个计数原理
1.(2020山东,3)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种 C.60种 D.30种
答案 C
2.(2020广东珠海三模,10)甲、乙、丙3人从1楼乘电梯去商场的3到9楼,每层楼最多下2人,则下电梯的方法有( )
A.210种 B.252种 C.343种 D.336种
答案 D
解析 分两种情况讨论:
①某个楼层只下1人,则3人下电梯的方法种数为 =210;②3人中有2人从一个楼层下,另1人从其他楼层选一个楼层下,此时,3人下电梯的方法种数为 =126.由分类加法计数原理可知,3人下电梯的方法种数为210+126=336.
3.(2020贵州毕节二诊,13)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,“赵爽弦图”如图所示,由四个全等的直角三角形和一个正方形构成,现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有 种(用数字作答).
答案 420
解析 由题意,假设五个区域分别为①②③④⑤,对于区域①②③,三个区域两两相邻,共有 =60种涂法;
对于区域④⑤,若④与②颜色相同,则⑤有3种
涂法,若④与②颜色不同,则④有2种涂法,⑤有
2种涂法,共有2×2=4种涂法,所以④⑤共有
3+4=7种涂法,则一共有60×7=420种涂法.
4.(2020山东潍坊二模,15)植树造林,绿化祖国.某班级义务劳动志愿者小组参加植树活动,准备在一抛物线形地块上的ABCDGFE七点处各种植一棵树苗,如图所示,其中A,B,C分别与E,F,G关于抛物线的对称轴对称,现有三种树苗,要求每种树苗至少种植一棵,且关于抛物线的对称轴对称的两点处必须种植同一种树苗,则共有不同的种植方法数是 (用数字作答).
答案 36
解析 由图形的对称性,相当于3种树苗种在A,B,C,D四个位置,有且仅有一种树苗重复,所以有 =3种方法.先从A,B,C,D中任选两个位置种植同一种树苗,有 =6种方法,再把另两种树苗种植在另两个位置上,有 =2种方法.则由分步乘法计数原理知,共有3×6×2=36种方法.
5.(2020山东泰安三模,15)甲、乙、丙、丁、戊五人去参加数学、物理、化学三科竞赛,每个同学只能参加一科竞赛,若每个同学可以自由选择,则不同的选择种数是 ;若甲和乙不参加同一科,甲和丙必须参加同一科,且这三科都有人参加,则不同的选择种数是 .(用数字作答)
答案 243 30
解析 若每个同学可以自由选择,由分步乘法计数原理可得,不同的选择种数是35=243;因为甲和乙不参加同一科,甲和丙必须参加同一科,所以有2,2,1和3,1,1两种分配方案.
由分类加法计数原理,可得不同的选择种数是18+12=30.
考向二
排列组合
6.(2020山东聊城二模,4)2020年是脱贫攻坚年,为顺利完成“两不愁,三保障”,即农村贫困人口不愁吃、不愁穿,农村贫困人口义务教育、基本医疗、住房安全有保障,某市拟派出6人组成三个帮扶队,每队两人,对脱贫任务较重的甲、乙、丙三县进行帮扶,则不同的派出方法种数共有( )
A.15 B.60 C.90 D.540
答案 C
解析 依题意,首先将人平均分成3组,再将三组进行全排列即可,所以所有可能的派出方法有 =90(种).
7.(2019北京海淀一模,理8)某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A层班级,生物在B层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
第一节 第二节 第三节 第四节
地理B层2班 化学A层3班 地理A层1班 化学A层4班
生物A层1班 化学B层2班 生物B层2班 历史B层1班
物理A层1班 生物A层3班 物理A层2班 生物A层4班
物理B层2班 生物B层1班 物理B层1班 物理A层4班
政治1班 物理A层3班 政治2班 政治3班
A.8种 B.10种 C.12种 D.14种
答案 B
解析 学校课表中每一节课都有物理A层可选,政治有三节课可选,生物B层只有二、三节可选,依据关键元素优先的原则,先安排生物B的“位置”,再安排政治的“位置”,接着安排物理的“位置”,三种科目安排好后,自习课随之确定,方法数为:3×2+2×2=10.
8.(2020湖南雅礼中学高三月考,5)中国古代儒家要求学生掌握六种基本才能:礼、乐、射、御、书、数,也称这六种才能为“六艺”.某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种 B.72种
C.96种 D.144种
答案 D
9.(2020天津和平区高三一模,8)在国际高峰论坛上,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为( )
A.378 B.306 C.268 D.198
答案 D
解析 分两种情况讨论.
①若选两个国内媒体一个国外媒体,有 =90种不同提问方式;②若选两个外国媒体一个国内媒体,有 =108种不同提问方式.
所以共有90+108=198种提问方式.
10.(2020山东济宁三模,15)5人并排站成一行,如果甲乙两人不相邻,那么不同的排法种数是 .(用数字作答);5人并排站成一行,甲乙两人之间恰好有一人的概率是 .(用数字作答)
考向三
二项式定理
11.(2020海南海南中学模拟,3)已知(2x-a)6(a是常数)的展开式中含x3项的系数为-160,则a=( )
答案 A
12.(2020全国Ⅰ,理8) (x+y)5的展开式中x3y3的系数为( )
A.5 B.10 C.15 D.20
答案 C
13.(多选)(2020海南三亚模拟,10)对于 的展开式,下列说法正确的是( )
A.展开式共有6项
B.展开式中的常数项是-240
C.展开式中各项系数之和为1
D.展开式中的二项式系数之和为64
答案 CD
14.(2020山东德州二模,7)(x2-x-a)5的展开式的各项系数之和为-32,则该展开式中含x9项的系数是( )
A.-15 B.-5 C.5 D.15
答案 B
解析 ∵(x2-x-a)5的展开式的各项系数之和为-32,令x=1,可得(12-1-a)5=-32,故(-a)5=-32,得a=2.
故(x2-x-a)5=(x2-x-2)5=(x-2)5(x+1)5,设(x-2)5展开式的通项公式为
同课章节目录
