专题六 6.4.2 随机变量及其分布 课件(共64张PPT)
文档属性
| 名称 | 专题六 6.4.2 随机变量及其分布 课件(共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 01:06:38 | ||
图片预览











文档简介
(共64张PPT)
6.4.2 随机变量及其分布
第三部分
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
1.超几何分布
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=
,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*.
2.二项分布
一般地,在n次独立重复试验中,事件A发生的次数为X,设每次试验中事件A发生的概率为p,则P(X=k)= pkqn-k,其中03.正态分布
一般地,如果对于任何实数a,b(aφμ,σ(x)dx,则称X的分布为正态分布.正态分布完全由参数μ和σ确定,因此正态分布常记作N(μ,σ2).如果随机变量X服从正态分布,则记为X~N(μ,σ2).满足正态分布的三个基本概率的值是:①P(μ-σ②P(μ-2σ4.离散型随机变量的分布列
设离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,则称下表为离散型随机变量X的分布列.
X x1 x2 x3 … xi … xn
P p1 p2 p3 … pi … pn
关键能力 学案突破
热点一
依据频率求概率的综合问题
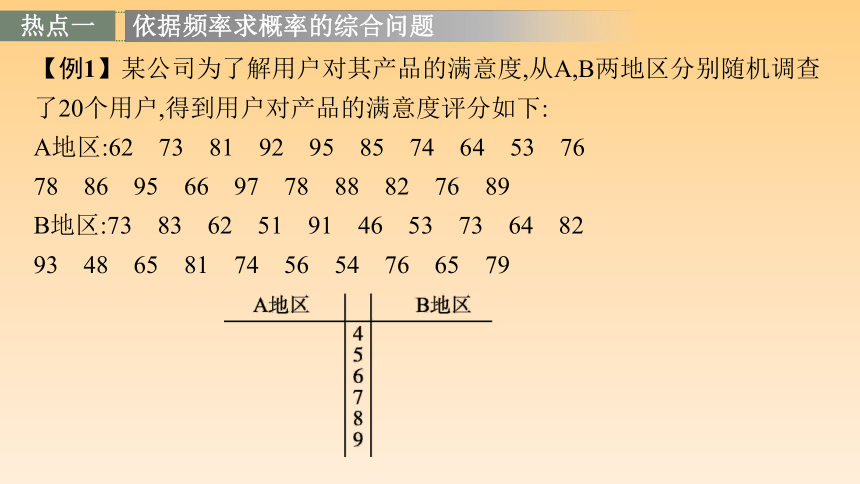
【例1】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 低于70分 70分到89分 不低于90分
满意度等级 不满意 满意 非常满意
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
解 (1)两地区用户满意度评分的茎叶图如图.通过茎叶图可以看出,A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值;A地区用户满意度评分比较集中,B地区用户满意度评分比较分散.
(2)记CA1表示事件:“A地区用户的满意度等级为满意或非常满意”;CA2表示事件:“A地区用户的满意度等级为非常满意”;CB1表示事件:“B地区用户的满意度等级为不满意”;CB2表示事件:“B地区用户的满意度等级为满意”,则CA1与CB1独立,CA2与CB2独立,CB1与CB2互斥,C=CB1CA1∪CB2CA2.
P(C)=P(CB1CA1∪CB2CA2)=P(CB1CA1)+P(CB2CA2)
=P(CB1)P(CA1)+P(CB2)P(CA2).由所给数据得CA1,CA2,CB1,CB2发生的频率分
解题心得频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,在实际问题中,常用事件发生的频率作为概率的估计值.频率本身是随机的,而概率是一个确定的数,是客观存在的,因此概率与每次试验无关.
(1)利用基本概念:①互斥事件不可能同时发生;②对立事件是互斥事件,且必须有一个要发生.
(2)利用集合的观点来判断:设事件A与B所含的结果组成的集合分别是A,B,全集为I.①事件A与B互斥,即集合A∩B= ;②事件A与B对立,即集合A∩B= ,且A∪B=I,也即A= IB或B= IA.
(3)对立事件是针对两个事件来说的,而互斥事件则可以是多个事件间的关系.
(4)如果A1,A2,…,An中任何两个都是互斥事件,那么我们就说A1,A2,…,An彼此互斥.
(5)若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
应用互斥事件的概率加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求其对立事件的概率.
(6)求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和;二是先求其对立事件的概率,然后再应用公式P(A)=1-P( )求解.
【对点训练1】(2019北京卷,理17)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元) 支付方式 (0,1 000] (1 000,2 000] 大于2 000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2 000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2 000 元的人数有变化 说明理由.
解 (1)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.所以从全校学生中随机抽取1人,该学生上个月A,B两种支付方式都使用的概率估计为
(2)X的所有可能值为0,1,2.记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”.由题设知,事
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(3)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2 000元”.
假设样本仅使用A的学生中,本月支付金额大于2 000 元的人数没有变化,
答案示例1:可以认为有变化.理由如下:P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2 000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
热点二
离散型随机变量的分布列
1.相互独立事件、互斥事件的概率及分布列
【例2】(2020山东济宁三模,20)过去五年,我国的扶贫工作进入了“精准扶贫”阶段.目前“精准扶贫”覆盖了全部贫困人口,东部帮西部,全国一盘棋的扶贫格局逐渐形成.到2020年底全国830个贫困县都将脱贫摘帽,最后4 335万贫困人口将全部脱贫,这将超过全球其他国家过去30年脱贫人口的总和.2020年是我国打赢脱贫攻坚战收官之年,越是到关键时刻,更应该强调“精准”.为落实“精准扶贫”政策,某扶贫小组,为一家“对点帮扶”农户引种了一种新的经济农作物,并指导该农户于2020年初开始种植.已知该经济农作物每年每亩的种植成本为1 000元,根据前期各方面调查发现,该经济农作物的市场价格和亩产量均具有随机性,且两者互不影响,其具体情况如下表:
该经济农作物亩产量(kg) 900 1 200
概率 0.5 0.5
该经济农作物市场价格(元/kg) 15 20
概率 0.4 0.6
(1)设2020年该农户种植该经济农作物一亩的纯收入为X元,求X的分布列;
(2)若该农户从2020年开始,连续三年种植该经济农作物,假设三年内各方面条件基本不变,求这三年中该农户种植该经济农作物一亩至少有两年的纯收入不少于16 000元的概率;
(3)2020年全国脱贫标准约为人均纯收入4 000元.假设该农户是一个四口之家,且该农户在2020年的家庭所有支出与其他收入正好相抵,能否凭这一亩经济农作物的纯收入,预测该农户在2020年底可以脱贫 并说明理由.
解 (1)由题意知1 200×20-1 000=23 000,1 200×15-1 000=17 000,
900×20-1 000=17 000,900×15-1 000=12 500,
所以X的所有可能取值为:23 000,17 000,12 500.
设A表示事件“作物产量为900 kg”,则P(A)=0.5;B表示事件“作物市场价格为15元/kg”,则P(B)=0.4.
X 23 000 17 000 12 500
P 0.3 0.5 0.2
(2)设C表示事件“种植该农作物一亩一年的纯收入不少于16 000元”,则P(C)=P(X>16 000)=P(X=23 000)+P(X=17 000)=0.3+0.5=0.8,设这三年中有Y年的纯收入不少于16 000元,则有Y~B(3,0.8),所以这三年中至少有两年的纯收入不少于16 000元的概率为
(3)由(1)知,2020年该农户种植该经济农作物一亩的预计纯收入为E(X)=23 000×0.3+17 000×0.5+12 500×0.2=17 900(元), >4 000,凭这一亩经济农作物的纯收入,该农户的人均纯收入超过了国家脱贫标准,所以能预测该农户在2020年底可以脱贫.
解题心得求复杂事件概率的2种方法
(1)直接法:正确分析复杂事件的构成,将复杂事件转化为几个彼此互斥事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少,则可利用其对立事件进行求解,对于“至少”“至多”等问题往往用这种方法求解.
【对点训练2】(2020江苏盐城模拟,18)为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费.(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量ξ,求ξ的分布列和数学期望E(ξ).
解 (1)根据题意,分别记“甲所付租车费0元、1元、2元”为事件A1,A2,A3,它们彼此互斥,且P(A1)=0.4,P(A2)=0.5,所以 P(A3)=1-0.4-0.5=0.1;分别记“乙所付租车费0元、1元、2元”为事件B1,B2,B3,它们彼此互斥,且P(B1)=0.5,
P(B2)=0.3,所以P(B3)=1-0.5-0.3=0.2.
由题知,A1,A2,A3与B1,B2,B3相互独立,记甲、乙两人所付租车费相同为事件M,则M=A1B1∪A2B2∪A3B3,所以P(M)=P(A1)P(B1)+P(A2)P(B2)+P(A3)P(B3)
=0.4×0.5+0.5×0.3+0.1×0.2=0.2+0.15+0.02=0.37.
(2)据题意,ξ的可能取值为0,1,2,3,4,P(ξ=0)=P(A1)P(B1)=0.2;
P(ξ=1)=P(A1)P(B2)+P(A2)P(B1)=0.4×0.3+0.5×0.5=0.37;
P(ξ=2)=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)
=0.4×0.2+0.5×0.3+0.1×0.5=0.28;
P(ξ=3)=P(A2)P(B3)+P(A3)P(B2)=0.5×0.2+0.1×0.3=0.13;
P(ξ=4)=P(A3)P(B3)=0.1×0.2=0.02.
所以ξ的分布列为:
ξ 0 1 2 3 4
P 0.2 0.37 0.28 0.13 0.02
数学期望E(ξ)=0×0.2+1×0.37+2×0.28+3×0.13+4×0.02=1.4.
2.超几何分布
【例3】(2020北京东城模拟,17)体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:℃)平均在36 ℃~37 ℃之间即为正常体温,超过37.1 ℃即为发热.发热状态下,不同体温可分成以下三种发热类型,低热:37.1≤T≤38;高热:3840.
某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温,记录如下:
(1)请你计算住院期间该患者体温不低于39 ℃的各天体温平均值;
(2)在19~23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“α项目”的检查,记X为高热体温下做“α项目”检查的天数,试求X的分布列与数学期望;
(3)抗生素治疗一般在服药后2~8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
抗生素 使用情况 没有使用 使用“抗生素A”治疗 使用“抗生素B”治疗
日期 12日 13日 14日 15日 16日 17日 18日 19日
体温(℃) 38.7 39.4 39.7 40.1 39.9 39.2 38.9 39.0
抗生素 使用情况 使用“抗生素C”治疗 没有使用
日期 20日 21日 22日 23日 24日 25日 26日
体温(℃) 38.4 38.0 37.6 37.1 36.8 36.6 36.3
所以,患者体温不低于39 ℃的各天体温平均值为39.55 ℃.
(2)X的所有可能取值为0,1,2.
则X的分布列为:
(3)说明“抗生素B”治疗效果最佳可使用如下理由:自使用“抗生素B”开始治疗后,体温才开始稳定下降,且使用“抗生素B”治疗当天共降温0.7 ℃,是单日降温效果最好的一天,故“抗生素B”治疗效果最佳.
说明“抗生素C”治疗效果最佳可使用如下理由:①“抗生素B”使用期间先连续两天降温1.0 ℃又回升0.1 ℃,“抗生素C”使用期间持续降温共计1.4 ℃,说明“抗生素C”降温效果最好,故“抗生素C”治疗效果最佳.
②“抗生素B”治疗期间,平均体温约为39.03 ℃,方差约为0.015 6;“抗生素C”治疗期间,平均体温约为38 ℃,方差约为0.106 7,“抗生素C”治疗期间体温离散程度大,说明存在某个时间节点降温效果明显,故“抗生素C”治疗效果最佳.
解题心得1.求超几何分布分布列的步骤
第一步,验证随机变量服从超几何分布,并确定参数N,M,n的值;
第二步,根据超几何分布的概率计算公式计算出随机变量取每一个值时的概率;
第三步,用表格的形式列出分布列.
2.本例第(3)问是一个开放性问题,答案不唯一,得出结论抗生素B或C降温效果最好都可以,只要说出合理的理由即可.
【对点训练3】(2020黑龙江大庆实验中学二模,19)2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100],例如:10点04分,记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1 000辆车通过该收费点,估计在9:46~10:22之间通过的车辆数(结果保留到整数).
参考数据:若T~N(μ,σ2),则①P(μ-σ②P(μ-2σ解 (1)这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为(30×0.005+50×0.015+70×0.020+90×0.010)×20=64,即10点04分.
(2)结合频率分布直方图和分层抽样的方法可知:抽取的10辆车中,
在10:00前通过的车辆数就是位于时间分组中在[20,60)这一区间内的车辆数,即(0.005+0.015)×20×10=4,所以X的可能取值为0,1,2,3,4.
所以X的分布列为
(3)由(1)可得μ=64,σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+
(90-64)2×0.2=324,所以σ=18,
估计在9:46~10:22这一时间段内通过的车辆数,也就是当463.二项分布
【例4】(2020北京朝阳一模,18)某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了80位患者和100位非患者,用该试剂盒分别对他们进行检测,结果如下:
非患者的检测结果 人数 患者的检测结果 人数
阳性 1 阳性 76
阴性 99 阴性 4
(1)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(2)从该地区患者中随机选取3人,各检测一次,假设每位患者的检测结果相互独立,以X表示检测结果为阳性的患者人数,利用(1)中所得概率,求X的分布列和数学期望;
(3)假设该地区有10万人,患病率为0.01.从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过0.5 并说明理由.
解 (1)由题意知,80位患者中有76位用该试剂盒检测一次,结果为阳性.
所以从该地区患者中随机选取一位,用该试剂盒检测一次,结果为阳性的概
所以X的分布列为
解题心得对于实际问题中的随机变量X,如果能够断定它服从二项分布B(n,p),那么其概率、期望与方差可直接利用公式P(X=k)= pk(1-p)n-k
(k=0,1,2,…,n),E(X)=np,D(X)=np(1-p)求得,因此,熟记二项分布的相关公式,可以避免烦琐的运算过程,提高运算速度和准确度.
【对点训练4】一年之计在于春,一天之计在于晨,春天是播种的季节,是希望的开端,某种植户对一块地的n(n∈N*)个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为 ,且每粒种子是否发芽相互独立,对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当n取何值时,有3个坑要补播种的概率最大 最大概率为多少
(2)当n=4时,用X表示要补播种的坑的个数,求X的分布列与数学期望.
所以X的分布列为
4.正态分布
【例5】(2020安徽池州三模,19)某市教学研究室为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三理科数学试卷的得分情况进行了调研.从全市参加考试的理科考生中随机抽取了100名考生的数学成绩(满分150分),将数据分成9组:[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差σ=20,以频率值作为概率估计值.
(1)根据频率分布直方图,求抽取的100名理科考生数学成绩的平均分 及众数y;
(2)用频率估计概率,从该市所有高三理科考生的数学成绩中随机抽取3个,记理科数学成绩位于区间[100,120)内的个数为Y,求Y的分布列及数学期望E(Y);
(3)从该市高三理科数学考试成绩中任意抽取一份,记其成绩为X,依据以下不等式评判(P表示对应事件的概率):①P(μ-σ评判规则:若至少满足以上两个不等式,则给予这套试卷好评,否则差评.试问这套试卷得到好评还是差评
∴Y的分布列为:
(3)记该市高三考生的理科数学成绩为X,由(1)可知,μ= =105,又σ=20,
则μ-σ=105-20=85,μ+σ=105+20=125,μ-2σ=105-2×20=65,
μ+2σ=105+2×20=145,μ-3σ=105-3×20=45,μ+3σ=105+3×20=165,
∴P(μ-σ=0.67<0.682 6,
P(μ-2σ0.954 4,
P(μ-3σ0.997 3,符合②③,不符合①,
∴这套试卷得到好评.
解题心得服从N(μ,σ2)的随机变量X在某个区间内取值的概率的求法
(1)利用P(μ-σ(2)充分利用正态曲线的对称性和曲线与x轴之间的面积为1这些特殊性质求解.
【对点训练5】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,
μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①试说明上述监控生产过程方法的合理性;
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
②下面是检验员在一天内抽取的16个零件的尺寸:
解 (1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 3,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 7,故X~B(16,0.002 7).因此P(X≥1)=1- P(X=0)=1-0.997 316≈0.042 3.X的数学期望为
E(X)=16×0.002 7=0.043 2.
(2)①如果生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有
0.002 7,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.042 3,发生的概率很小.因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.
6.4.2 随机变量及其分布
第三部分
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
1.超几何分布
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=
,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*.
2.二项分布
一般地,在n次独立重复试验中,事件A发生的次数为X,设每次试验中事件A发生的概率为p,则P(X=k)= pkqn-k,其中0
一般地,如果对于任何实数a,b(a
设离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,则称下表为离散型随机变量X的分布列.
X x1 x2 x3 … xi … xn
P p1 p2 p3 … pi … pn
关键能力 学案突破
热点一
依据频率求概率的综合问题
【例1】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 低于70分 70分到89分 不低于90分
满意度等级 不满意 满意 非常满意
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
解 (1)两地区用户满意度评分的茎叶图如图.通过茎叶图可以看出,A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值;A地区用户满意度评分比较集中,B地区用户满意度评分比较分散.
(2)记CA1表示事件:“A地区用户的满意度等级为满意或非常满意”;CA2表示事件:“A地区用户的满意度等级为非常满意”;CB1表示事件:“B地区用户的满意度等级为不满意”;CB2表示事件:“B地区用户的满意度等级为满意”,则CA1与CB1独立,CA2与CB2独立,CB1与CB2互斥,C=CB1CA1∪CB2CA2.
P(C)=P(CB1CA1∪CB2CA2)=P(CB1CA1)+P(CB2CA2)
=P(CB1)P(CA1)+P(CB2)P(CA2).由所给数据得CA1,CA2,CB1,CB2发生的频率分
解题心得频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,在实际问题中,常用事件发生的频率作为概率的估计值.频率本身是随机的,而概率是一个确定的数,是客观存在的,因此概率与每次试验无关.
(1)利用基本概念:①互斥事件不可能同时发生;②对立事件是互斥事件,且必须有一个要发生.
(2)利用集合的观点来判断:设事件A与B所含的结果组成的集合分别是A,B,全集为I.①事件A与B互斥,即集合A∩B= ;②事件A与B对立,即集合A∩B= ,且A∪B=I,也即A= IB或B= IA.
(3)对立事件是针对两个事件来说的,而互斥事件则可以是多个事件间的关系.
(4)如果A1,A2,…,An中任何两个都是互斥事件,那么我们就说A1,A2,…,An彼此互斥.
(5)若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
应用互斥事件的概率加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求其对立事件的概率.
(6)求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和;二是先求其对立事件的概率,然后再应用公式P(A)=1-P( )求解.
【对点训练1】(2019北京卷,理17)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付金额(元) 支付方式 (0,1 000] (1 000,2 000] 大于2 000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2 000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2 000 元的人数有变化 说明理由.
解 (1)由题意知,样本中仅使用A的学生有18+9+3=30人,仅使用B的学生有10+14+1=25人,A,B两种支付方式都不使用的学生有5人.故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.所以从全校学生中随机抽取1人,该学生上个月A,B两种支付方式都使用的概率估计为
(2)X的所有可能值为0,1,2.记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”.由题设知,事
所以X的分布列为
X 0 1 2
P 0.24 0.52 0.24
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.
(3)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2 000元”.
假设样本仅使用A的学生中,本月支付金额大于2 000 元的人数没有变化,
答案示例1:可以认为有变化.理由如下:P(E)比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2 000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,所以无法确定有没有变化.
热点二
离散型随机变量的分布列
1.相互独立事件、互斥事件的概率及分布列
【例2】(2020山东济宁三模,20)过去五年,我国的扶贫工作进入了“精准扶贫”阶段.目前“精准扶贫”覆盖了全部贫困人口,东部帮西部,全国一盘棋的扶贫格局逐渐形成.到2020年底全国830个贫困县都将脱贫摘帽,最后4 335万贫困人口将全部脱贫,这将超过全球其他国家过去30年脱贫人口的总和.2020年是我国打赢脱贫攻坚战收官之年,越是到关键时刻,更应该强调“精准”.为落实“精准扶贫”政策,某扶贫小组,为一家“对点帮扶”农户引种了一种新的经济农作物,并指导该农户于2020年初开始种植.已知该经济农作物每年每亩的种植成本为1 000元,根据前期各方面调查发现,该经济农作物的市场价格和亩产量均具有随机性,且两者互不影响,其具体情况如下表:
该经济农作物亩产量(kg) 900 1 200
概率 0.5 0.5
该经济农作物市场价格(元/kg) 15 20
概率 0.4 0.6
(1)设2020年该农户种植该经济农作物一亩的纯收入为X元,求X的分布列;
(2)若该农户从2020年开始,连续三年种植该经济农作物,假设三年内各方面条件基本不变,求这三年中该农户种植该经济农作物一亩至少有两年的纯收入不少于16 000元的概率;
(3)2020年全国脱贫标准约为人均纯收入4 000元.假设该农户是一个四口之家,且该农户在2020年的家庭所有支出与其他收入正好相抵,能否凭这一亩经济农作物的纯收入,预测该农户在2020年底可以脱贫 并说明理由.
解 (1)由题意知1 200×20-1 000=23 000,1 200×15-1 000=17 000,
900×20-1 000=17 000,900×15-1 000=12 500,
所以X的所有可能取值为:23 000,17 000,12 500.
设A表示事件“作物产量为900 kg”,则P(A)=0.5;B表示事件“作物市场价格为15元/kg”,则P(B)=0.4.
X 23 000 17 000 12 500
P 0.3 0.5 0.2
(2)设C表示事件“种植该农作物一亩一年的纯收入不少于16 000元”,则P(C)=P(X>16 000)=P(X=23 000)+P(X=17 000)=0.3+0.5=0.8,设这三年中有Y年的纯收入不少于16 000元,则有Y~B(3,0.8),所以这三年中至少有两年的纯收入不少于16 000元的概率为
(3)由(1)知,2020年该农户种植该经济农作物一亩的预计纯收入为E(X)=23 000×0.3+17 000×0.5+12 500×0.2=17 900(元), >4 000,凭这一亩经济农作物的纯收入,该农户的人均纯收入超过了国家脱贫标准,所以能预测该农户在2020年底可以脱贫.
解题心得求复杂事件概率的2种方法
(1)直接法:正确分析复杂事件的构成,将复杂事件转化为几个彼此互斥事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少,则可利用其对立事件进行求解,对于“至少”“至多”等问题往往用这种方法求解.
【对点训练2】(2020江苏盐城模拟,18)为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费.(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量ξ,求ξ的分布列和数学期望E(ξ).
解 (1)根据题意,分别记“甲所付租车费0元、1元、2元”为事件A1,A2,A3,它们彼此互斥,且P(A1)=0.4,P(A2)=0.5,所以 P(A3)=1-0.4-0.5=0.1;分别记“乙所付租车费0元、1元、2元”为事件B1,B2,B3,它们彼此互斥,且P(B1)=0.5,
P(B2)=0.3,所以P(B3)=1-0.5-0.3=0.2.
由题知,A1,A2,A3与B1,B2,B3相互独立,记甲、乙两人所付租车费相同为事件M,则M=A1B1∪A2B2∪A3B3,所以P(M)=P(A1)P(B1)+P(A2)P(B2)+P(A3)P(B3)
=0.4×0.5+0.5×0.3+0.1×0.2=0.2+0.15+0.02=0.37.
(2)据题意,ξ的可能取值为0,1,2,3,4,P(ξ=0)=P(A1)P(B1)=0.2;
P(ξ=1)=P(A1)P(B2)+P(A2)P(B1)=0.4×0.3+0.5×0.5=0.37;
P(ξ=2)=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)
=0.4×0.2+0.5×0.3+0.1×0.5=0.28;
P(ξ=3)=P(A2)P(B3)+P(A3)P(B2)=0.5×0.2+0.1×0.3=0.13;
P(ξ=4)=P(A3)P(B3)=0.1×0.2=0.02.
所以ξ的分布列为:
ξ 0 1 2 3 4
P 0.2 0.37 0.28 0.13 0.02
数学期望E(ξ)=0×0.2+1×0.37+2×0.28+3×0.13+4×0.02=1.4.
2.超几何分布
【例3】(2020北京东城模拟,17)体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:℃)平均在36 ℃~37 ℃之间即为正常体温,超过37.1 ℃即为发热.发热状态下,不同体温可分成以下三种发热类型,低热:37.1≤T≤38;高热:38
某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温,记录如下:
(1)请你计算住院期间该患者体温不低于39 ℃的各天体温平均值;
(2)在19~23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“α项目”的检查,记X为高热体温下做“α项目”检查的天数,试求X的分布列与数学期望;
(3)抗生素治疗一般在服药后2~8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
抗生素 使用情况 没有使用 使用“抗生素A”治疗 使用“抗生素B”治疗
日期 12日 13日 14日 15日 16日 17日 18日 19日
体温(℃) 38.7 39.4 39.7 40.1 39.9 39.2 38.9 39.0
抗生素 使用情况 使用“抗生素C”治疗 没有使用
日期 20日 21日 22日 23日 24日 25日 26日
体温(℃) 38.4 38.0 37.6 37.1 36.8 36.6 36.3
所以,患者体温不低于39 ℃的各天体温平均值为39.55 ℃.
(2)X的所有可能取值为0,1,2.
则X的分布列为:
(3)说明“抗生素B”治疗效果最佳可使用如下理由:自使用“抗生素B”开始治疗后,体温才开始稳定下降,且使用“抗生素B”治疗当天共降温0.7 ℃,是单日降温效果最好的一天,故“抗生素B”治疗效果最佳.
说明“抗生素C”治疗效果最佳可使用如下理由:①“抗生素B”使用期间先连续两天降温1.0 ℃又回升0.1 ℃,“抗生素C”使用期间持续降温共计1.4 ℃,说明“抗生素C”降温效果最好,故“抗生素C”治疗效果最佳.
②“抗生素B”治疗期间,平均体温约为39.03 ℃,方差约为0.015 6;“抗生素C”治疗期间,平均体温约为38 ℃,方差约为0.106 7,“抗生素C”治疗期间体温离散程度大,说明存在某个时间节点降温效果明显,故“抗生素C”治疗效果最佳.
解题心得1.求超几何分布分布列的步骤
第一步,验证随机变量服从超几何分布,并确定参数N,M,n的值;
第二步,根据超几何分布的概率计算公式计算出随机变量取每一个值时的概率;
第三步,用表格的形式列出分布列.
2.本例第(3)问是一个开放性问题,答案不唯一,得出结论抗生素B或C降温效果最好都可以,只要说出合理的理由即可.
【对点训练3】(2020黑龙江大庆实验中学二模,19)2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100],例如:10点04分,记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1 000辆车通过该收费点,估计在9:46~10:22之间通过的车辆数(结果保留到整数).
参考数据:若T~N(μ,σ2),则①P(μ-σ
(2)结合频率分布直方图和分层抽样的方法可知:抽取的10辆车中,
在10:00前通过的车辆数就是位于时间分组中在[20,60)这一区间内的车辆数,即(0.005+0.015)×20×10=4,所以X的可能取值为0,1,2,3,4.
所以X的分布列为
(3)由(1)可得μ=64,σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+
(90-64)2×0.2=324,所以σ=18,
估计在9:46~10:22这一时间段内通过的车辆数,也就是当46
【例4】(2020北京朝阳一模,18)某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了80位患者和100位非患者,用该试剂盒分别对他们进行检测,结果如下:
非患者的检测结果 人数 患者的检测结果 人数
阳性 1 阳性 76
阴性 99 阴性 4
(1)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(2)从该地区患者中随机选取3人,各检测一次,假设每位患者的检测结果相互独立,以X表示检测结果为阳性的患者人数,利用(1)中所得概率,求X的分布列和数学期望;
(3)假设该地区有10万人,患病率为0.01.从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过0.5 并说明理由.
解 (1)由题意知,80位患者中有76位用该试剂盒检测一次,结果为阳性.
所以从该地区患者中随机选取一位,用该试剂盒检测一次,结果为阳性的概
所以X的分布列为
解题心得对于实际问题中的随机变量X,如果能够断定它服从二项分布B(n,p),那么其概率、期望与方差可直接利用公式P(X=k)= pk(1-p)n-k
(k=0,1,2,…,n),E(X)=np,D(X)=np(1-p)求得,因此,熟记二项分布的相关公式,可以避免烦琐的运算过程,提高运算速度和准确度.
【对点训练4】一年之计在于春,一天之计在于晨,春天是播种的季节,是希望的开端,某种植户对一块地的n(n∈N*)个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为 ,且每粒种子是否发芽相互独立,对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当n取何值时,有3个坑要补播种的概率最大 最大概率为多少
(2)当n=4时,用X表示要补播种的坑的个数,求X的分布列与数学期望.
所以X的分布列为
4.正态分布
【例5】(2020安徽池州三模,19)某市教学研究室为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三理科数学试卷的得分情况进行了调研.从全市参加考试的理科考生中随机抽取了100名考生的数学成绩(满分150分),将数据分成9组:[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差σ=20,以频率值作为概率估计值.
(1)根据频率分布直方图,求抽取的100名理科考生数学成绩的平均分 及众数y;
(2)用频率估计概率,从该市所有高三理科考生的数学成绩中随机抽取3个,记理科数学成绩位于区间[100,120)内的个数为Y,求Y的分布列及数学期望E(Y);
(3)从该市高三理科数学考试成绩中任意抽取一份,记其成绩为X,依据以下不等式评判(P表示对应事件的概率):①P(μ-σ
∴Y的分布列为:
(3)记该市高三考生的理科数学成绩为X,由(1)可知,μ= =105,又σ=20,
则μ-σ=105-20=85,μ+σ=105+20=125,μ-2σ=105-2×20=65,
μ+2σ=105+2×20=145,μ-3σ=105-3×20=45,μ+3σ=105+3×20=165,
∴P(μ-σ
P(μ-2σ
P(μ-3σ
∴这套试卷得到好评.
解题心得服从N(μ,σ2)的随机变量X在某个区间内取值的概率的求法
(1)利用P(μ-σ
【对点训练5】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,
μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①试说明上述监控生产过程方法的合理性;
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
②下面是检验员在一天内抽取的16个零件的尺寸:
解 (1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 3,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 7,故X~B(16,0.002 7).因此P(X≥1)=1- P(X=0)=1-0.997 316≈0.042 3.X的数学期望为
E(X)=16×0.002 7=0.043 2.
(2)①如果生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有
0.002 7,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.042 3,发生的概率很小.因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.
同课章节目录
