第4练 函数的图象与性质 课件(共55张PPT)
文档属性
| 名称 | 第4练 函数的图象与性质 课件(共55张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 02:14:53 | ||
图片预览


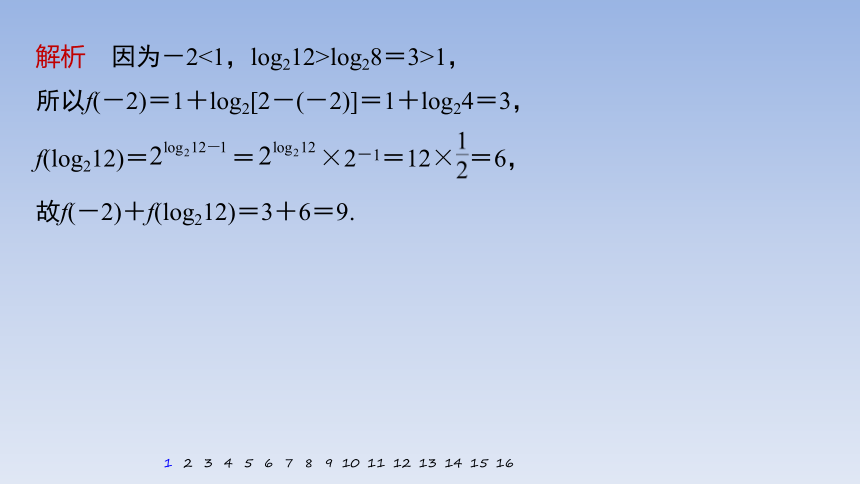








文档简介
(共55张PPT)
函数的图象与性质
第4练
专项典题精练
高考汇编
A.3 B.6 C.9 D.12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 因为-2<1,log212>log28=3>1,
所以f(-2)=1+log2[2-(-2)]=1+log24=3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
f(log212)= = ×2-1=12× =6,
故f(-2)+f(log212)=3+6=9.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)为奇函数,排除A;
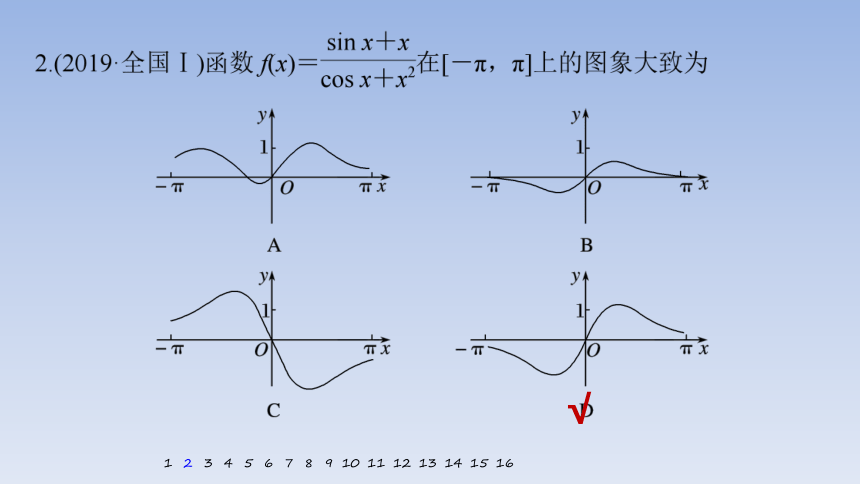
3.(2020·全国Ⅱ)设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),
∴f(x)为奇函数,故排除A,C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(2020·新高考全国Ⅰ)若定义在R上的奇函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是
A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为函数f(x)为定义在R上的奇函数,则f(0)=0.
又f(x)在(-∞,0)上单调递减,且f(2)=0,
画出函数f(x)的大致图象如图(1)所示,
则函数f(x-1)的大致图象如图(2)所示.
当x≤0时,要满足xf(x-1)≥0,则f(x-1)≤0,得-1≤x≤0.
当x>0时,要满足xf(x-1)≥0,则f(x-1)≥0,得1≤x≤3.
故满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2017·全国Ⅰ)已知函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是
A.[-2,2] B.[-1,1]
C.[0,4] D.[1,3]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x).
∵f(1)=-1,∴f(-1)=-f(1)=1.
故由-1≤f(x-2)≤1,
得f(1)≤f(x-2)≤f(-1).
又f(x)在(-∞,+∞)上单调递减,
∴-1≤x-2≤1,∴1≤x≤3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于f(x+1)为奇函数,所以函数f(x)的图象关于点(1,0)对称,
即有f(x)+f(2-x)=0,
所以f(1)+f(2-1)=0,
得f(1)=0,即a+b=0. ①
由于f(x+2)为偶函数,
所以函数f(x)的图象关于直线x=2对称,
即有f(x)-f(4-x)=0,
所以f(0)+f(3)=-f(2)+f(1)=-4a-b+a+b=-3a=6. ②
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
根据①②可得a=-2,b=2,
所以当x∈[1,2]时,f(x)=-2x2+2.
根据函数f(x)的图象关于直线x=2对称,且关于点(1,0)对称,
可得函数f(x)的周期为4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由函数f(x)满足f(x+4)=f(x)(x∈R),可知函数f(x)的周期是4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2021·新高考全国Ⅰ)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 方法一 (定义法)
因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-x)=f(x)对任意的x∈R恒成立,
所以(-x)3(a·2-x-2x)=x3(a·2x-2-x)对任意的x∈R恒成立,
所以x3(a-1)(2x+2-x)=0对任意的x∈R恒成立,
所以a=1.
方法二 (取特殊值检验法)
因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-1)=f(1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
方法三 (转化法)
由题意知f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数.
设g(x)=x3,h(x)=a·2x-2-x,
因为g(x)=x3为奇函数,所以h(x)=a·2x-2-x为奇函数,
所以h(0)=a·20-2-0=0,解得a=1,
经检验,f(x)=x3(2x-2-x)为偶函数,
所以a=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(-∞,-3)∪(-3,0]
B.(-∞,-3)∪(-3,1]
C.(-3,0]
D.(-3,1]
√
∴f(x)的定义域为(-3,0].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.(2021·哈尔滨模拟)已知函数f(x)为奇函数,当x>0时,f(x)=log2(x+1)+ax,且f(-3)=a,则f(7)等于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x),f(-3)=-f(3)=a,则f(3)=-a,
∵当x>0时,f(x)=log2(x+1)+ax,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·临川一中模拟)已知函数y=f(x)的图象如图所示,则此函数可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x≠±1,
即f(x)的定义域为{x|x≠±1},在区间(0,1)上,
e-x-ex<0,x2+2|x|-3<0,f(x)>0,与所给图象不符;
在区间(0,1)上,ex-e-x>0,x2+2|x|-3<0,f(x)<0,
在区间(1,+∞)上,ex-e-x>0,x2+2|x|-3>0,f(x)>0,与所给图象不矛盾;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x≠±1,
即f(x)的定义域为{x|x≠±1},
当x→+∞时,f(x)→0,与所给图象不符;
在区间(0,1)上,e|x|-1-e1-|x|<0,x5-x<0,f(x)>0,与所给图象不符.
故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(-4,0)∪(4,+∞)
B.(-∞,-4)∪(0,4)
C.(-4,0)∪(0,4)
D.(-∞,-4)∪(4,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 函数f(x)为奇函数,则f(-x)=-f(x),
因为f(-4)=0,f(x)在(0,+∞)上单调递增,
则f(x)在(-∞,0)上单调递增,
所以由f(x)>0得-4由题知f(x)在(0,+∞)上单调递增,所以由f(x)<0得01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
所以f(-x)=sin(-x)ln(e-x+ex)=-sin xln(ex+e-x)=-f(x),
即函数f(x)为奇函数,其图象关于原点对称,故排除D,
当且仅当x=0时取等号,所以ln(ex+e-x)≥ln 2>ln 1=0,
当x∈[0,π)时,sin x≥0,
当x∈[π,2π)时,sin x≤0,
所以当x∈[0,π)时,f(x)≥0,
当x∈[π,2π)时,f(x)≤0,故排除A,B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵f(x)是奇函数,∴f(x)在(-2,0)上单调递减,且f(x)>0,
又f(0)=0,∴f(x)在(-2,2)上单调递减.
由f(x)的图象关于点(2,0)对称,
得f(x)=f[2-(2-x)]=-f[2+(2-x)]=-f(4-x),
又f(x)是奇函数,f(x)=-f(-x),
∴-f(-x)=-f(4-x),f(-x)=f(4-x),
即f(x)=f(4+x),
∴f(x)是周期函数,周期为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(-2)=f(2),且f(-2)=-f(2),
∴f(2)=f(-2)=0,
∴f(2k)=0,k∈Z.
f(x)在(-2,2)上单调递减,
则f(x)在(2 018,2 022)上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(2021·临沂模拟)若函数f(x)满足:
(1)对于任意实数x1,x2,当01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
lg x
解析 根据题意,若函数f(x)满足(1),则函数f(x)在区间(0,+∞)上单调递增,
若函数f(x)满足(2),可以考虑f(x)为对数函数,则f(x)可以为lg x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 已知定义在R上的函数f(x)满足
f(x+1)=f(x-1),
则f(x)=f(x+2),
所以函数f(x)是周期为2的周期函数,
其中a∈R,b>0且b≠1.
由f(-1)=f(1),可得-a+1=0,解得a=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
以基本初等函数为载体,考查函数的定义域、最值、奇偶性、单调性、周期性、分段函数求值或分段函数中参数的求解以及函数图象的识别,多以选择题、填空题的形式考查,难度属中档及以上.
一、函数的概念与表示
核心提炼
1.复合函数的定义域
(1)若f(x)的定义域为[m,n],则在f(g(x))中,m≤g(x)≤n,从中解得x的范围即为f(g(x))的定义域.
(2)若f(g(x))的定义域为[m,n],则由m≤x≤n确定的g(x)的范围即为f(x)的定义域.
2.分段函数
分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数值域的并集.
题号 1 7 9
二、函数的性质
核心提炼
1.函数的奇偶性
(1)定义:若函数的定义域关于原点对称,则有
f(x)是偶函数 f(-x)=f(x)=f(|x|);
f(x)是奇函数 f(-x)=-f(x).
(2)判断方法:定义法、图象法、奇偶函数性质法(如奇函数×奇函数是偶函数).
2.函数单调性判断方法:定义法、图象法、导数法.
3.函数图象的对称中心和对称轴
(1)若函数f(x)满足关系式f(a+x)=2b-f(a-x),则函数y=f(x)的图象关于点(a,b)对称.
(2)若函数f(x)满足关系式f(a+x)=f(b-x),则函数y=f(x)的图象关于直线x= 对称.
题号 3 4 5 6 8 10 12 14 15 16
三、函数的图象
核心提炼
1.作函数图象有两种基本方法:一是描点法;二是图象变换法,其中图象变换有平移变换、伸缩变换、对称变换.
2.由函数的解析式判断其图象的主要方法是利用函数的性质,如定义域、奇偶性、单调性等,以及利用函数图象上的特殊点排除不符合要求的图象.
题号 2 11 13
易错对点精补
A.是奇函数,且在(0,+∞)上单调递增
B.是奇函数,且在(0,+∞)上单调递减
C.是偶函数,且在(0,+∞)上单调递增
D.是偶函数,且在(0,+∞)上单调递减
√
1
2
3
4
5
6
解析 方法一 函数f(x)的定义域为(-∞,0)∪(0,+∞),
1
2
3
4
5
6
所以f(x)是奇函数.
又因为y=x3在(0,+∞)上单调递增,
所以f(x)在(0,+∞)上单调递增.
方法二 同方法一得f(x)是奇函数.
又f′(x)=(x3-x-3)′=3x2+3x-4>0,
所以f(x)在(0,+∞)上单调递增.
1
2
3
4
5
6
2.[T11补偿](2021·青岛模拟)已知函数f(x)的部分图象如图所示,则f(x)可能为
1
2
3
4
5
6
√
解析 由题图,知函数的定义域为R,函数的图象关于y轴对称,则函数为偶函数,
1
2
3
4
5
6
1
2
3
4
5
6
3.[T4补偿](2021·辽阳模拟)已知函数f(x)的定义域为R,f(x+4)是偶函数,f(6)=3,f(x)在(-∞,4]上单调递减,则不等式f(2x-4)<3的解集为
A.(4,6) B.(-∞,4)∪(6,+∞)
C.(-∞,3)∪(5,+∞) D.(3,5)
√
1
2
3
4
5
6
解析 因为f(x+4)是偶函数,
所以函数f(x)的图象关于直线x=4对称,
则f(6)=f(2)=3.
因为f(x)在(-∞,4]上单调递减,
所以f(x)在[4,+∞)上单调递增,
故f(2x-4)<3等价于2<2x-4<6,解得31
2
3
4
5
6
√
1
2
3
4
5
6
解析 因为f(x+1)=-f(x),所以f(x)的周期为2,
因为定义在R上的偶函数f(x)在[0,1]上单调递减,
所以由f(π)=1,f(2π)=2,
可得f(4-π)=1,f(2π-6)=2,且4-π,2π-6∈[0,1],
由1≤x≤2,得0≤2-x≤1,
所以原不等式组的解集为[π-2,8-2π].
1
2
3
4
5
6
5.[T14补偿](2021·张家口模拟)已知f(x)是R上的奇函数,且对x∈R,有f(x+2)=-f(x),当x∈(0,1)时,f(x)=2x-1,则f(log241)=________.
1
2
3
4
5
6
解析 由题意知,f(x+2)=-f(x),
则f[(x+2)+2]=-f(x+2)=f(x),
即f(x)是周期为4的周期函数,
又由5得f(log241)=f(log241-4)
=-f(log241-6)=f(6-log241).
∵6-log241∈(0,1),
1
2
3
4
5
6
6.[T15补偿](2021·湖南六校联考)请写出满足条件“f(x)≤f(1)对任意的x∈[0,1]恒成立,且f(x)在[0,1]上不是增函数”的一个函数_____________
_____________.
1
2
3
4
5
6
(答案不唯一)
函数的图象与性质
第4练
专项典题精练
高考汇编
A.3 B.6 C.9 D.12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 因为-2<1,log212>log28=3>1,
所以f(-2)=1+log2[2-(-2)]=1+log24=3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
f(log212)= = ×2-1=12× =6,
故f(-2)+f(log212)=3+6=9.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)为奇函数,排除A;
3.(2020·全国Ⅱ)设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵f(-x)=ln|-2x+1|-ln|-2x-1|=ln|2x-1|-ln|2x+1|=-f(x),
∴f(x)为奇函数,故排除A,C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(2020·新高考全国Ⅰ)若定义在R上的奇函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是
A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为函数f(x)为定义在R上的奇函数,则f(0)=0.
又f(x)在(-∞,0)上单调递减,且f(2)=0,
画出函数f(x)的大致图象如图(1)所示,
则函数f(x-1)的大致图象如图(2)所示.
当x≤0时,要满足xf(x-1)≥0,则f(x-1)≤0,得-1≤x≤0.
当x>0时,要满足xf(x-1)≥0,则f(x-1)≥0,得1≤x≤3.
故满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2017·全国Ⅰ)已知函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是
A.[-2,2] B.[-1,1]
C.[0,4] D.[1,3]
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x).
∵f(1)=-1,∴f(-1)=-f(1)=1.
故由-1≤f(x-2)≤1,
得f(1)≤f(x-2)≤f(-1).
又f(x)在(-∞,+∞)上单调递减,
∴-1≤x-2≤1,∴1≤x≤3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于f(x+1)为奇函数,所以函数f(x)的图象关于点(1,0)对称,
即有f(x)+f(2-x)=0,
所以f(1)+f(2-1)=0,
得f(1)=0,即a+b=0. ①
由于f(x+2)为偶函数,
所以函数f(x)的图象关于直线x=2对称,
即有f(x)-f(4-x)=0,
所以f(0)+f(3)=-f(2)+f(1)=-4a-b+a+b=-3a=6. ②
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
根据①②可得a=-2,b=2,
所以当x∈[1,2]时,f(x)=-2x2+2.
根据函数f(x)的图象关于直线x=2对称,且关于点(1,0)对称,
可得函数f(x)的周期为4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由函数f(x)满足f(x+4)=f(x)(x∈R),可知函数f(x)的周期是4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2021·新高考全国Ⅰ)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 方法一 (定义法)
因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-x)=f(x)对任意的x∈R恒成立,
所以(-x)3(a·2-x-2x)=x3(a·2x-2-x)对任意的x∈R恒成立,
所以x3(a-1)(2x+2-x)=0对任意的x∈R恒成立,
所以a=1.
方法二 (取特殊值检验法)
因为f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数,
所以f(-1)=f(1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
经检验,f(x)=x3(2x-2-x)为偶函数,所以a=1.
方法三 (转化法)
由题意知f(x)=x3(a·2x-2-x)的定义域为R,且是偶函数.
设g(x)=x3,h(x)=a·2x-2-x,
因为g(x)=x3为奇函数,所以h(x)=a·2x-2-x为奇函数,
所以h(0)=a·20-2-0=0,解得a=1,
经检验,f(x)=x3(2x-2-x)为偶函数,
所以a=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(-∞,-3)∪(-3,0]
B.(-∞,-3)∪(-3,1]
C.(-3,0]
D.(-3,1]
√
∴f(x)的定义域为(-3,0].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.(2021·哈尔滨模拟)已知函数f(x)为奇函数,当x>0时,f(x)=log2(x+1)+ax,且f(-3)=a,则f(7)等于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x),f(-3)=-f(3)=a,则f(3)=-a,
∵当x>0时,f(x)=log2(x+1)+ax,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·临川一中模拟)已知函数y=f(x)的图象如图所示,则此函数可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x≠±1,
即f(x)的定义域为{x|x≠±1},在区间(0,1)上,
e-x-ex<0,x2+2|x|-3<0,f(x)>0,与所给图象不符;
在区间(0,1)上,ex-e-x>0,x2+2|x|-3<0,f(x)<0,
在区间(1,+∞)上,ex-e-x>0,x2+2|x|-3>0,f(x)>0,与所给图象不矛盾;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x≠±1,
即f(x)的定义域为{x|x≠±1},
当x→+∞时,f(x)→0,与所给图象不符;
在区间(0,1)上,e|x|-1-e1-|x|<0,x5-x<0,f(x)>0,与所给图象不符.
故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(-4,0)∪(4,+∞)
B.(-∞,-4)∪(0,4)
C.(-4,0)∪(0,4)
D.(-∞,-4)∪(4,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 函数f(x)为奇函数,则f(-x)=-f(x),
因为f(-4)=0,f(x)在(0,+∞)上单调递增,
则f(x)在(-∞,0)上单调递增,
所以由f(x)>0得-4
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
所以f(-x)=sin(-x)ln(e-x+ex)=-sin xln(ex+e-x)=-f(x),
即函数f(x)为奇函数,其图象关于原点对称,故排除D,
当且仅当x=0时取等号,所以ln(ex+e-x)≥ln 2>ln 1=0,
当x∈[0,π)时,sin x≥0,
当x∈[π,2π)时,sin x≤0,
所以当x∈[0,π)时,f(x)≥0,
当x∈[π,2π)时,f(x)≤0,故排除A,B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵f(x)是奇函数,∴f(x)在(-2,0)上单调递减,且f(x)>0,
又f(0)=0,∴f(x)在(-2,2)上单调递减.
由f(x)的图象关于点(2,0)对称,
得f(x)=f[2-(2-x)]=-f[2+(2-x)]=-f(4-x),
又f(x)是奇函数,f(x)=-f(-x),
∴-f(-x)=-f(4-x),f(-x)=f(4-x),
即f(x)=f(4+x),
∴f(x)是周期函数,周期为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(-2)=f(2),且f(-2)=-f(2),
∴f(2)=f(-2)=0,
∴f(2k)=0,k∈Z.
f(x)在(-2,2)上单调递减,
则f(x)在(2 018,2 022)上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(2021·临沂模拟)若函数f(x)满足:
(1)对于任意实数x1,x2,当0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
lg x
解析 根据题意,若函数f(x)满足(1),则函数f(x)在区间(0,+∞)上单调递增,
若函数f(x)满足(2),可以考虑f(x)为对数函数,则f(x)可以为lg x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 已知定义在R上的函数f(x)满足
f(x+1)=f(x-1),
则f(x)=f(x+2),
所以函数f(x)是周期为2的周期函数,
其中a∈R,b>0且b≠1.
由f(-1)=f(1),可得-a+1=0,解得a=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
以基本初等函数为载体,考查函数的定义域、最值、奇偶性、单调性、周期性、分段函数求值或分段函数中参数的求解以及函数图象的识别,多以选择题、填空题的形式考查,难度属中档及以上.
一、函数的概念与表示
核心提炼
1.复合函数的定义域
(1)若f(x)的定义域为[m,n],则在f(g(x))中,m≤g(x)≤n,从中解得x的范围即为f(g(x))的定义域.
(2)若f(g(x))的定义域为[m,n],则由m≤x≤n确定的g(x)的范围即为f(x)的定义域.
2.分段函数
分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数值域的并集.
题号 1 7 9
二、函数的性质
核心提炼
1.函数的奇偶性
(1)定义:若函数的定义域关于原点对称,则有
f(x)是偶函数 f(-x)=f(x)=f(|x|);
f(x)是奇函数 f(-x)=-f(x).
(2)判断方法:定义法、图象法、奇偶函数性质法(如奇函数×奇函数是偶函数).
2.函数单调性判断方法:定义法、图象法、导数法.
3.函数图象的对称中心和对称轴
(1)若函数f(x)满足关系式f(a+x)=2b-f(a-x),则函数y=f(x)的图象关于点(a,b)对称.
(2)若函数f(x)满足关系式f(a+x)=f(b-x),则函数y=f(x)的图象关于直线x= 对称.
题号 3 4 5 6 8 10 12 14 15 16
三、函数的图象
核心提炼
1.作函数图象有两种基本方法:一是描点法;二是图象变换法,其中图象变换有平移变换、伸缩变换、对称变换.
2.由函数的解析式判断其图象的主要方法是利用函数的性质,如定义域、奇偶性、单调性等,以及利用函数图象上的特殊点排除不符合要求的图象.
题号 2 11 13
易错对点精补
A.是奇函数,且在(0,+∞)上单调递增
B.是奇函数,且在(0,+∞)上单调递减
C.是偶函数,且在(0,+∞)上单调递增
D.是偶函数,且在(0,+∞)上单调递减
√
1
2
3
4
5
6
解析 方法一 函数f(x)的定义域为(-∞,0)∪(0,+∞),
1
2
3
4
5
6
所以f(x)是奇函数.
又因为y=x3在(0,+∞)上单调递增,
所以f(x)在(0,+∞)上单调递增.
方法二 同方法一得f(x)是奇函数.
又f′(x)=(x3-x-3)′=3x2+3x-4>0,
所以f(x)在(0,+∞)上单调递增.
1
2
3
4
5
6
2.[T11补偿](2021·青岛模拟)已知函数f(x)的部分图象如图所示,则f(x)可能为
1
2
3
4
5
6
√
解析 由题图,知函数的定义域为R,函数的图象关于y轴对称,则函数为偶函数,
1
2
3
4
5
6
1
2
3
4
5
6
3.[T4补偿](2021·辽阳模拟)已知函数f(x)的定义域为R,f(x+4)是偶函数,f(6)=3,f(x)在(-∞,4]上单调递减,则不等式f(2x-4)<3的解集为
A.(4,6) B.(-∞,4)∪(6,+∞)
C.(-∞,3)∪(5,+∞) D.(3,5)
√
1
2
3
4
5
6
解析 因为f(x+4)是偶函数,
所以函数f(x)的图象关于直线x=4对称,
则f(6)=f(2)=3.
因为f(x)在(-∞,4]上单调递减,
所以f(x)在[4,+∞)上单调递增,
故f(2x-4)<3等价于2<2x-4<6,解得3
2
3
4
5
6
√
1
2
3
4
5
6
解析 因为f(x+1)=-f(x),所以f(x)的周期为2,
因为定义在R上的偶函数f(x)在[0,1]上单调递减,
所以由f(π)=1,f(2π)=2,
可得f(4-π)=1,f(2π-6)=2,且4-π,2π-6∈[0,1],
由1≤x≤2,得0≤2-x≤1,
所以原不等式组的解集为[π-2,8-2π].
1
2
3
4
5
6
5.[T14补偿](2021·张家口模拟)已知f(x)是R上的奇函数,且对x∈R,有f(x+2)=-f(x),当x∈(0,1)时,f(x)=2x-1,则f(log241)=________.
1
2
3
4
5
6
解析 由题意知,f(x+2)=-f(x),
则f[(x+2)+2]=-f(x+2)=f(x),
即f(x)是周期为4的周期函数,
又由5
=-f(log241-6)=f(6-log241).
∵6-log241∈(0,1),
1
2
3
4
5
6
6.[T15补偿](2021·湖南六校联考)请写出满足条件“f(x)≤f(1)对任意的x∈[0,1]恒成立,且f(x)在[0,1]上不是增函数”的一个函数_____________
_____________.
1
2
3
4
5
6
(答案不唯一)
同课章节目录
