山东省聊城市某重点高中2012-2013学年下学期高一3月模块测试数学试题
文档属性
| 名称 | 山东省聊城市某重点高中2012-2013学年下学期高一3月模块测试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 204.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-11 21:30:49 | ||
图片预览



文档简介
聊城市某重点高中2012-2013学年下学期高一3月模块测试
数学试题
第I卷(选择题)
一、选择题
1.如果函数在区间上是减少的,那么实数的取值范围是 ( )
A. B. C. D.
2.已知平面向量的集合到的映射为,其中为常向量,若映射满足对任意恒成立,则用坐标可能是
A. B. C. D.
3.设,都是非零向量,命题P:,命题Q:的夹角为钝角。则P是Q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知集合,则
A. B. C. D.
5.平面内有定点A、B及动点P,设命题甲是“|PA|+|PB|是定值”,命题乙是“点P的轨迹是以A、B为焦点的椭圆”,那么甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知是定义在R上的函数,且对任意,都有,又,则等于( )
A. B. C. D.
7.设全集U是实数集R,M={x|x2>4},N={x|1图1
A.{x|-2≤x<1} B.{x|-2≤x≤2}
C.{x|1<x≤2} D.{x|x<2}
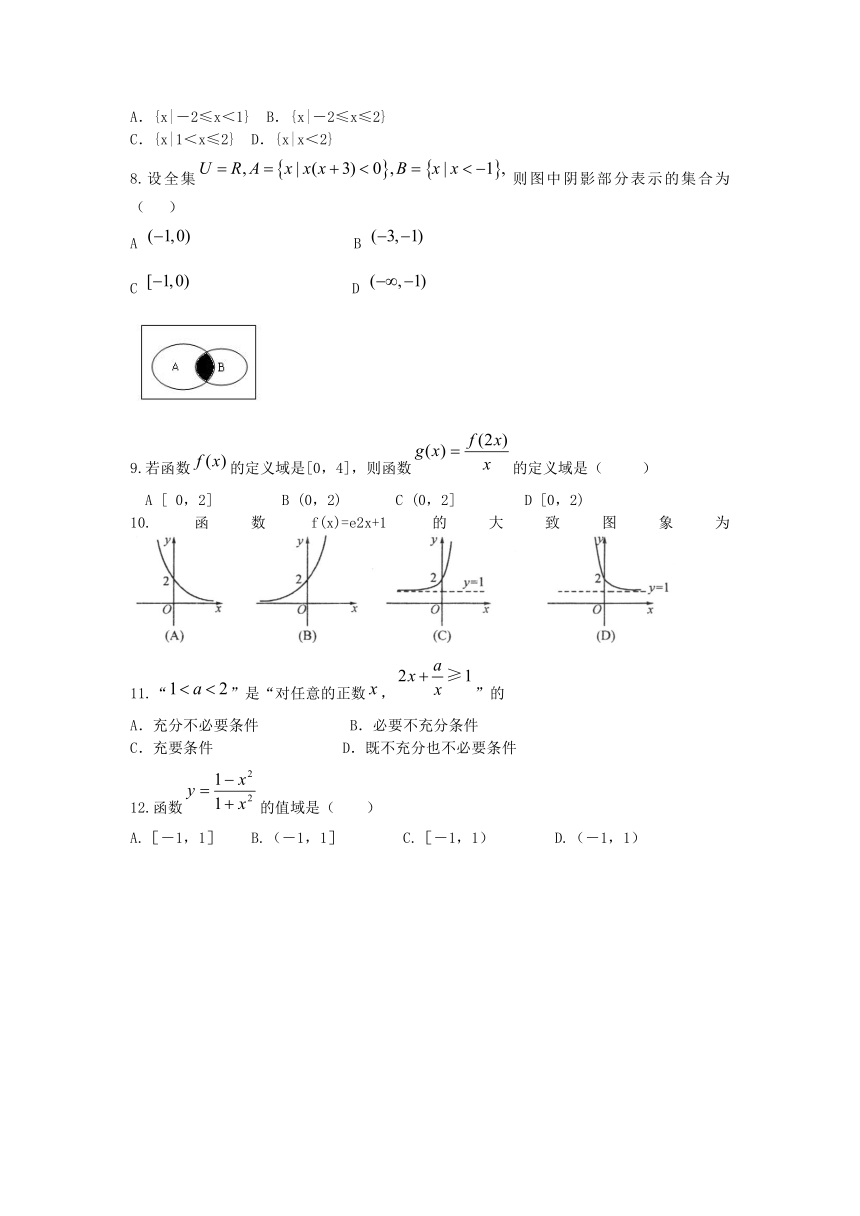
8.设全集则图中阴影部分表示的集合为( )
A B
C D
9.若函数的定义域是[0,4],则函数的定义域是( )
A [ 0,2] B (0,2) C (0,2] D [0,2)
10.函数f(x)=e2x+1的大致图象为
11.“”是“对任意的正数,”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.函数的值域是( )
A.[-1,1] B.(-1,1] C.[-1,1) D.(-1,1)
第II卷(非选择题)
二、填空题
13. 若奇函数在定义域上递减,且,则的取值范围是___________________
14.,则x=
15.已知集合A={1,2,3,4,5},集合B={1,2,4,6},则= ▲ .
16.函数y=的定义域是
三、解答题
17.(本小题满分12分)
已知函数处取得极值2。
(1)求函数的表达式;
(2)当满足什么条件时,函数在区间上单调递增?
(3)若为图象上任意一点,直线与的图象切于点P,求直线的斜率的取值范围。
18.(本小题满分12分)已知函数.
(1)写出的单调区间;(2)解不等式; (3)设,求在上的最大值.
19.(本小题满分16分)
已知函数在区间上的值域为
(Ⅰ)求的值;
(Ⅱ)若关于的函数在区间上为单调函数,求实数的取值范围.
20.(12分)设命题,命题,若“”为假命题,“”为真命题,求实数的取值范围
21.(本题满分16分)已知函数(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设,解关于x的不等式;.
22.本小题满分14分)已知函数,,其中R .(1)讨论的单调性;(2)若在其定义域内为增函数,求正实数的取值范围;(3)设函数, 当时,若存在,对于任意的,总有成立,求实数的取值范围.
高一数学试卷答案
1.B 2.D 3.B 4.D 5.B 6.C 7.C 8.B 9.C 10.C 11.A 12.B
13.
14.
15.{1,2,4}
16.
17.(1)因为 ····················2分
而函数在处取得极值2,
所以, 即 解得
所以即为所求 ····················4分
(2)由(1)知
令得:
则的增减性如下表:
(-∞,-1)
(-1,1)
(1,+∞)
负
正
负
可知,的单调增区间是[-1,1],
所以
所以当时,函数在区间上单调递增。 ·········9分
(3)由条件知,过的图象上一点P的切线的斜率为:
令,则,
此时,的图象性质知:
当时,;
当时,
所以,直线的斜率的取值范围是 ····················12分
18.解(1): ……………2
的单调递增区间是; 单调递减区间是. …4
解(2):
不等式的解集为 ………………………8
(3)解:(1)当时,是上的增函数,此时在上的最大值是 ………………………10
(2)当时,在上是增函数,在上是减函数,此时在上的最大值是;
综上,当时,在上的最大值是;当时,在上的最大值是。 ………………………12
19.解:(Ⅰ)∵a>0,∴所以抛物线开口向上且对称轴为x=1.
∴函数f(x)在[2,3]上单调递增.
由条件得
,即,解得a=1,b=0. ………………………6分
(Ⅱ)由(Ⅰ)知a=1,b=0.
∴f(x)=x2(2x+2,从而g(x)=x2((m+3)x+2. ………………………8分
若g(x)在[2,4]上递增,则对称轴,解得m≤1;……………………11分
若g(x)在[2,4]上递减,则对称轴,解得m≥5,……………………14分
故所求m的取值范围是m≥5或m≤1. …………………………………………………16分
20.:由,得,
因此,或,
由,得
因此或,
因为是的必要条件,所以,
即.
因此解得.
21.解:(1)将,得
8
(2)不等式即为,
即 10
①当 12
②当 14
③. 16
22.解:(Ⅰ)的定义域为,且, ………1分
①当时,,在上单调递增; ………2分
②当时,由,得;由,得;
故在上单调递减,在上单调递增. ………3分
(Ⅱ),的定义域为,
因为在其定义域内为增函数,所以,
………5分
而,当且仅当时取等号,所以 ………7分
(Ⅲ)当时,,
由得或,当时,;当时,.
所以在上, ………8分
而在上的最大值为
有……12分
所以实数的取值范围是 …………14分
数学试题
第I卷(选择题)
一、选择题
1.如果函数在区间上是减少的,那么实数的取值范围是 ( )
A. B. C. D.
2.已知平面向量的集合到的映射为,其中为常向量,若映射满足对任意恒成立,则用坐标可能是
A. B. C. D.
3.设,都是非零向量,命题P:,命题Q:的夹角为钝角。则P是Q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知集合,则
A. B. C. D.
5.平面内有定点A、B及动点P,设命题甲是“|PA|+|PB|是定值”,命题乙是“点P的轨迹是以A、B为焦点的椭圆”,那么甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知是定义在R上的函数,且对任意,都有,又,则等于( )
A. B. C. D.
7.设全集U是实数集R,M={x|x2>4},N={x|1
A.{x|-2≤x<1} B.{x|-2≤x≤2}
C.{x|1<x≤2} D.{x|x<2}
8.设全集则图中阴影部分表示的集合为( )
A B
C D
9.若函数的定义域是[0,4],则函数的定义域是( )
A [ 0,2] B (0,2) C (0,2] D [0,2)
10.函数f(x)=e2x+1的大致图象为
11.“”是“对任意的正数,”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.函数的值域是( )
A.[-1,1] B.(-1,1] C.[-1,1) D.(-1,1)
第II卷(非选择题)
二、填空题
13. 若奇函数在定义域上递减,且,则的取值范围是___________________
14.,则x=
15.已知集合A={1,2,3,4,5},集合B={1,2,4,6},则= ▲ .
16.函数y=的定义域是
三、解答题
17.(本小题满分12分)
已知函数处取得极值2。
(1)求函数的表达式;
(2)当满足什么条件时,函数在区间上单调递增?
(3)若为图象上任意一点,直线与的图象切于点P,求直线的斜率的取值范围。
18.(本小题满分12分)已知函数.
(1)写出的单调区间;(2)解不等式; (3)设,求在上的最大值.
19.(本小题满分16分)
已知函数在区间上的值域为
(Ⅰ)求的值;
(Ⅱ)若关于的函数在区间上为单调函数,求实数的取值范围.
20.(12分)设命题,命题,若“”为假命题,“”为真命题,求实数的取值范围
21.(本题满分16分)已知函数(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设,解关于x的不等式;.
22.本小题满分14分)已知函数,,其中R .(1)讨论的单调性;(2)若在其定义域内为增函数,求正实数的取值范围;(3)设函数, 当时,若存在,对于任意的,总有成立,求实数的取值范围.
高一数学试卷答案
1.B 2.D 3.B 4.D 5.B 6.C 7.C 8.B 9.C 10.C 11.A 12.B
13.
14.
15.{1,2,4}
16.
17.(1)因为 ····················2分
而函数在处取得极值2,
所以, 即 解得
所以即为所求 ····················4分
(2)由(1)知
令得:
则的增减性如下表:
(-∞,-1)
(-1,1)
(1,+∞)
负
正
负
可知,的单调增区间是[-1,1],
所以
所以当时,函数在区间上单调递增。 ·········9分
(3)由条件知,过的图象上一点P的切线的斜率为:
令,则,
此时,的图象性质知:
当时,;
当时,
所以,直线的斜率的取值范围是 ····················12分
18.解(1): ……………2
的单调递增区间是; 单调递减区间是. …4
解(2):
不等式的解集为 ………………………8
(3)解:(1)当时,是上的增函数,此时在上的最大值是 ………………………10
(2)当时,在上是增函数,在上是减函数,此时在上的最大值是;
综上,当时,在上的最大值是;当时,在上的最大值是。 ………………………12
19.解:(Ⅰ)∵a>0,∴所以抛物线开口向上且对称轴为x=1.
∴函数f(x)在[2,3]上单调递增.
由条件得
,即,解得a=1,b=0. ………………………6分
(Ⅱ)由(Ⅰ)知a=1,b=0.
∴f(x)=x2(2x+2,从而g(x)=x2((m+3)x+2. ………………………8分
若g(x)在[2,4]上递增,则对称轴,解得m≤1;……………………11分
若g(x)在[2,4]上递减,则对称轴,解得m≥5,……………………14分
故所求m的取值范围是m≥5或m≤1. …………………………………………………16分
20.:由,得,
因此,或,
由,得
因此或,
因为是的必要条件,所以,
即.
因此解得.
21.解:(1)将,得
8
(2)不等式即为,
即 10
①当 12
②当 14
③. 16
22.解:(Ⅰ)的定义域为,且, ………1分
①当时,,在上单调递增; ………2分
②当时,由,得;由,得;
故在上单调递减,在上单调递增. ………3分
(Ⅱ),的定义域为,
因为在其定义域内为增函数,所以,
………5分
而,当且仅当时取等号,所以 ………7分
(Ⅲ)当时,,
由得或,当时,;当时,.
所以在上, ………8分
而在上的最大值为
有……12分
所以实数的取值范围是 …………14分
同课章节目录
