第9练 导数与不等式证明 课件(共26张PPT)
文档属性
| 名称 | 第9练 导数与不等式证明 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:20:43 | ||
图片预览








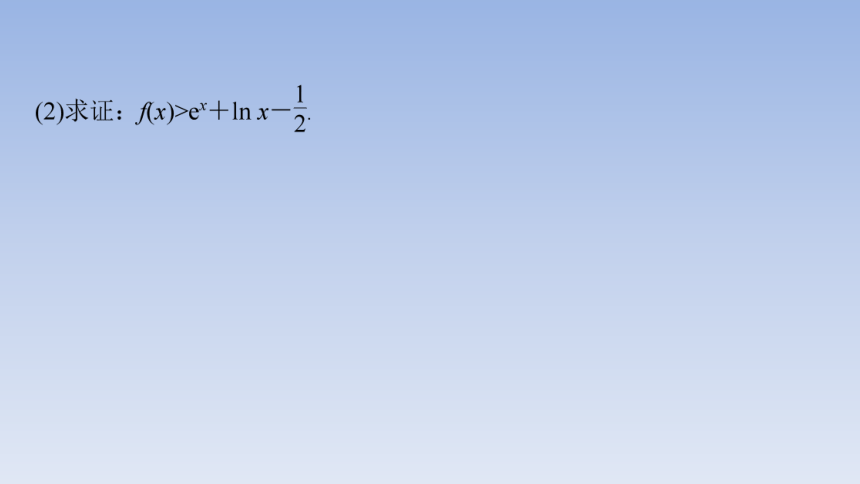
文档简介
(共26张PPT)
导数与不等式证明
第9练
考情分析
导数与不等式证明是高考考查的重点知识,在解答题中一般会考查函数的单调性、极值和最值的综合运用,试题难度较大,多次以压轴题出现.
一、单变量函数不等式的证明
例1 (2020·全国Ⅱ)已知函数f(x)=sin2xsin 2x.
(1)讨论f(x)在区间(0,π)的单调性;
解 f′(x)=2sin xcos xsin 2x+2sin2xcos 2x=2sin xsin 3x.
证明 因为f(0)=f(π)=0,
而f(x)是周期为π的周期函数,
证明 由于
=|sin3xsin32x…sin32nx|
=|sin x||sin2xsin32x…sin32n-1xsin 2nx||sin22nx|
=|sin x||f(x)f(2x)…f(2n-1x)||sin22nx|
≤|f(x)f(2x)…f(2n-1x)|,
规律方法 用导数证明不等式一般有以下的方法:
(1)构造函数法.
(2)由结论出发,通过对函数变形,证明不等式.
(3)分成两个函数进行研究.
(4)利用图象的特点证明不等式.
(5)利用放缩法证明不等式.
跟踪训练1 (2021·赣州模拟)已知函数f(x)=xex(其中e为自然对数的底数).
(1)求函数f(x)的最小值;
解 因为f(x)=xex,
所以f′(x)=(x+1)ex,
当x<-1时,f′(x)=(x+1)ex<0,f(x)单调递减,
当x>-1时,f′(x)=(x+1)ex>0,f(x)单调递增,
g′(1)=e-1>0,
例2 (2018·全国Ⅰ)已知函数f(x)= -x+aln x.
(1)讨论f(x)的单调性;
二、双变量函数不等式的证明
解 f(x)的定义域为(0,+∞),
①若a≤2,则f′(x)≤0,
当且仅当a=2,x=1时,f′(x)=0,
所以f(x)在(0,+∞)上单调递减.
②若a>2,令f′(x)=0,得
证明 由(1)知,f(x)存在两个极值点当且仅当a>2.
由于f(x)的两个极值点x1,x2满足x2-ax+1=0,
所以x1x2=1,不妨设x11.
由(1)知,g(x)在(0,+∞)上单调递减.
又g(1)=0,从而当x∈(1,+∞)时,g(x)<0.
规律方法 (1)含参不等式的证明方法:对于含参数的不等式,如果易分离参数、构造函数,直接转化为求函数的最值问题,否则应进行分类讨论,在解题过程中,必要时可作出函数图象(草图),利用数形结合求解.
(2)破解含双参不等式的证明的关键:一是转化,即由已知条件入手,寻找双参所满足的关系式,并把含双参的不等式转化为含单参的不等式;二是构造函数,借助导数,判断函数的单调性,从而求其值;三是回归含双参的不等式的证明,把所求的最值应用到含参的不等式中,即可证得结果.
跟踪训练2 (2021·盐城模拟)已知函数f(x)=x2- -a.
(1)若f(x)≥0,求实数a的取值范围;
所以函数r(x)=x3+ln x-1在(0,+∞)上单调递增.
又r(1)=0,列表如下:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ↘ 极小值 ↗
因为f(x)≥0,即1-a≥0,所以a≤1.
所以a的取值范围是(-∞,1].
(2)若函数f(x)有两个零点x1,x2,证明:x1x2<1.
证明 不妨设x1由(1)可得,函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
因为f(x1)=f(x2)=0,
导数与不等式证明
第9练
考情分析
导数与不等式证明是高考考查的重点知识,在解答题中一般会考查函数的单调性、极值和最值的综合运用,试题难度较大,多次以压轴题出现.
一、单变量函数不等式的证明
例1 (2020·全国Ⅱ)已知函数f(x)=sin2xsin 2x.
(1)讨论f(x)在区间(0,π)的单调性;
解 f′(x)=2sin xcos xsin 2x+2sin2xcos 2x=2sin xsin 3x.
证明 因为f(0)=f(π)=0,
而f(x)是周期为π的周期函数,
证明 由于
=|sin3xsin32x…sin32nx|
=|sin x||sin2xsin32x…sin32n-1xsin 2nx||sin22nx|
=|sin x||f(x)f(2x)…f(2n-1x)||sin22nx|
≤|f(x)f(2x)…f(2n-1x)|,
规律方法 用导数证明不等式一般有以下的方法:
(1)构造函数法.
(2)由结论出发,通过对函数变形,证明不等式.
(3)分成两个函数进行研究.
(4)利用图象的特点证明不等式.
(5)利用放缩法证明不等式.
跟踪训练1 (2021·赣州模拟)已知函数f(x)=xex(其中e为自然对数的底数).
(1)求函数f(x)的最小值;
解 因为f(x)=xex,
所以f′(x)=(x+1)ex,
当x<-1时,f′(x)=(x+1)ex<0,f(x)单调递减,
当x>-1时,f′(x)=(x+1)ex>0,f(x)单调递增,
g′(1)=e-1>0,
例2 (2018·全国Ⅰ)已知函数f(x)= -x+aln x.
(1)讨论f(x)的单调性;
二、双变量函数不等式的证明
解 f(x)的定义域为(0,+∞),
①若a≤2,则f′(x)≤0,
当且仅当a=2,x=1时,f′(x)=0,
所以f(x)在(0,+∞)上单调递减.
②若a>2,令f′(x)=0,得
证明 由(1)知,f(x)存在两个极值点当且仅当a>2.
由于f(x)的两个极值点x1,x2满足x2-ax+1=0,
所以x1x2=1,不妨设x1
由(1)知,g(x)在(0,+∞)上单调递减.
又g(1)=0,从而当x∈(1,+∞)时,g(x)<0.
规律方法 (1)含参不等式的证明方法:对于含参数的不等式,如果易分离参数、构造函数,直接转化为求函数的最值问题,否则应进行分类讨论,在解题过程中,必要时可作出函数图象(草图),利用数形结合求解.
(2)破解含双参不等式的证明的关键:一是转化,即由已知条件入手,寻找双参所满足的关系式,并把含双参的不等式转化为含单参的不等式;二是构造函数,借助导数,判断函数的单调性,从而求其值;三是回归含双参的不等式的证明,把所求的最值应用到含参的不等式中,即可证得结果.
跟踪训练2 (2021·盐城模拟)已知函数f(x)=x2- -a.
(1)若f(x)≥0,求实数a的取值范围;
所以函数r(x)=x3+ln x-1在(0,+∞)上单调递增.
又r(1)=0,列表如下:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ↘ 极小值 ↗
因为f(x)≥0,即1-a≥0,所以a≤1.
所以a的取值范围是(-∞,1].
(2)若函数f(x)有两个零点x1,x2,证明:x1x2<1.
证明 不妨设x1
因为f(x1)=f(x2)=0,
同课章节目录
