第13练 三角函数的图象与性质 课件(共69张PPT)
文档属性
| 名称 | 第13练 三角函数的图象与性质 课件(共69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:25:14 | ||
图片预览








文档简介
(共69张PPT)
三角函数的图象与性质
第13练
专项典题精练
高考汇编
A.f(x)=|cos 2x| B.f(x)=|sin 2x|
C.f(x)=cos|x| D.f(x)=sin|x|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
C中,函数f(x)=cos|x|=cos x的周期为2π,故C不正确;
在x≥0和x<0时,f(x)均以2π为周期,但在整个定义域上f(x)不是周期函数,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
再将所得曲线上所有点的横坐标扩大到原来的2倍,得到f(x)的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
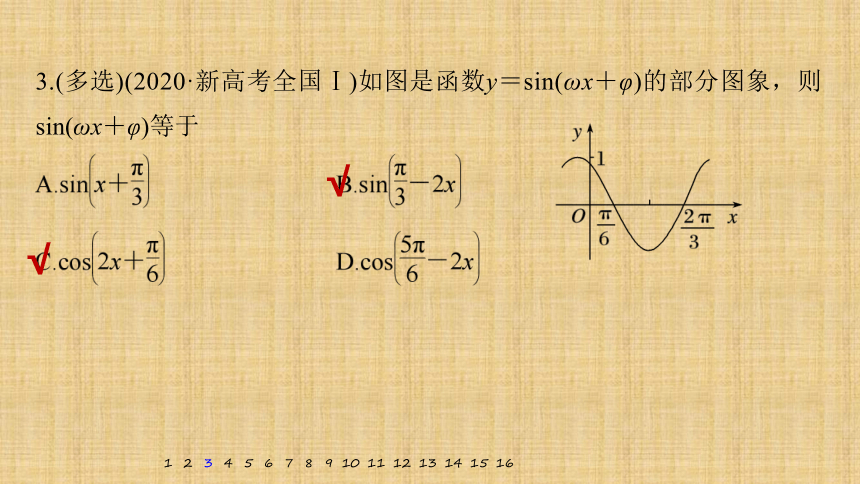
3.(多选)(2020·新高考全国Ⅰ)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
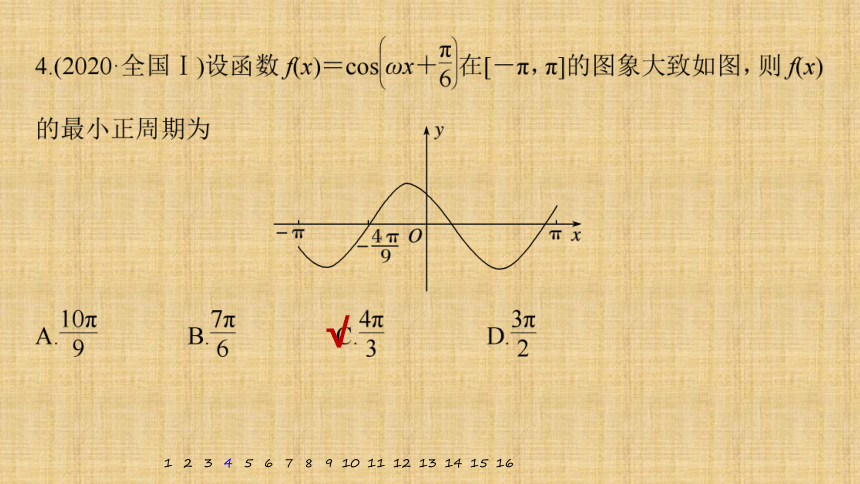
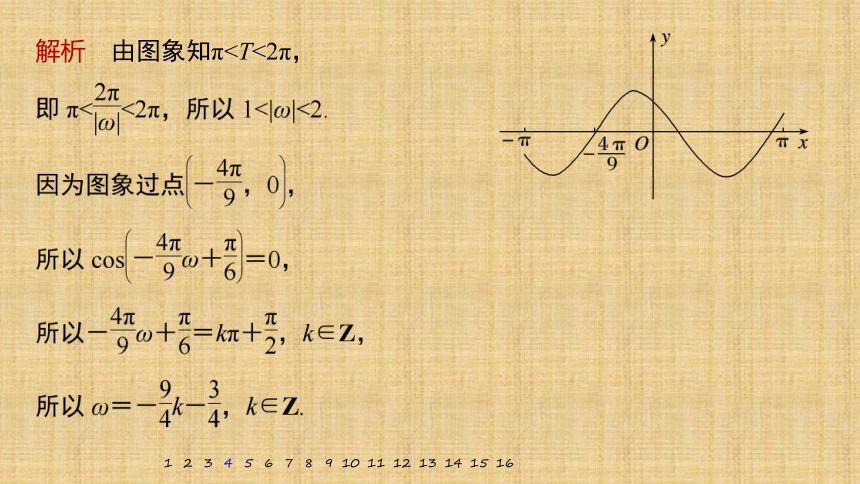
解析 由图象知π1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2018·全国Ⅱ)若f(x)=cos x-sin x在[-a,a]上是减函数,则a的最大值是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f(x)=cos x-sin x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①f(x)在(0,2π)上有且仅有3个极大值点;
②f(x)在(0,2π)上有且仅有2个极小值点;
其中所有正确结论的编号是
A.①④ B.②③ C.①②③ D.①③④
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,根据题意知,xA≤2π根据图象可知函数f(x)在(0,2π)有且仅有3个极大值点,所以①正确;
但可能会有3个极小值点,所以②错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
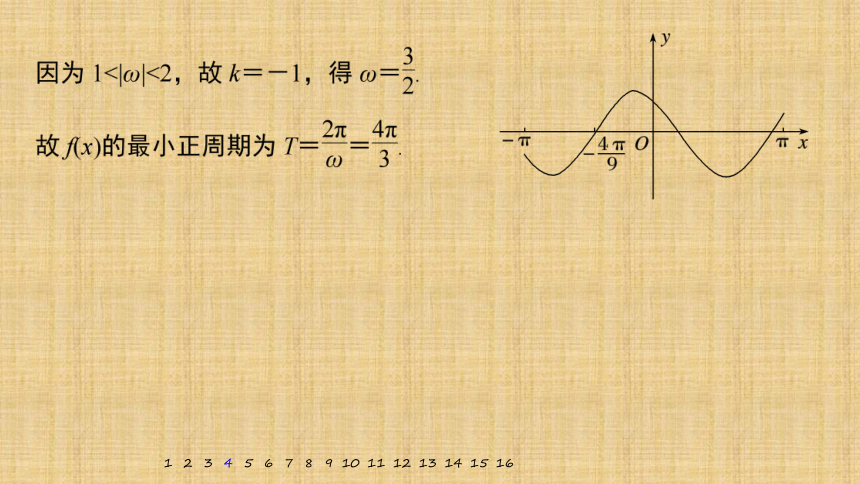
得T=π,所以ω=2,所以f(x)=2cos(2x+φ).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即[f(x)-1]·f(x)>0,可得f(x)>1或f(x)<0,
所以满足题意的最小正整数x为2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 函数f(x)=sin(2x+φ),其中φ∈(0,2π),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·南昌模拟)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,下列有关它的描述正确的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 根据f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(2021·哈尔滨模拟)已知函数f(x)=sin ωx+cos ωx(ω>0),若f(x)在(-π,π)上有且只有3个零点,则ω的取值范围为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若f(x)在(-π,π)上有且只有3个零点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故函数g(x)在该区间上先增后减,故A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.f(x)的周期为π
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D.f(2 020)+f(2 021)=0
√
√
√
则选项A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则选项D正确.
15.(2021·盐城模拟)若函数f(x)=sin(2x+φ)为偶函数,则φ的一个值为___.
(写出一个即可)
解析 依题意知,函数f(x)=sin(2x+φ)为偶函数,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
③f(x)在(0,2π)上有且仅有1个最小值点;
④f(x)的值域为[-1,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以π为函数f(x)的周期.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以函数f(x)在(0,2π)上有且只有1个最小值点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故③正确,④错误.
考情分析
练后疑难精讲
高考必考内容,重点考查三角函数的图象与性质及三角函数图象变换的正用、逆用,多以选择题和填空题的形式考查,也在解答题中出现,难度中等.
一、三角函数的图象及变换
核心提炼
图象变换
(先平移后伸缩)
y=Asin(ωx+φ).
(先伸缩后平移)
y=Asin(ωx+φ).
题号 2 11 13
二、三角函数的解析式
核心提炼
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
(3)求φ,常用的方法有:五点法、特殊点法.
题号 3 4 8 14
三、三角函数的性质
核心提炼
三角函数的常用结论
(1)y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数;
对称轴方程可由ωx+φ=kπ(k∈Z)求得.
(3)y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数.
题号 1 5 6 7 9 10 12 15 16
易错对点精补
1.[T1补偿](多选)(2021·锦州模拟)已知函数f(x)=|cos x|-sin|x|,则下列结论正确的是
A.f(x)是偶函数
B.f(x)是周期函数
1
2
3
4
5
6
D.f(x)的最大值为1
√
√
解析 对于A,f(x)的定义域为R,
且f(-x)=|cos(-x)|-sin|-x|=|cos x|-sin|x|=f(x),所以f(x)为偶函数,故A正确;
对于B,因为y=|cos x|是周期为π的周期函数,y=sin|x|关于y轴对称,不是周期函数,
所以f(x)=|cos x|-sin|x|不是周期函数,故B错误;
1
2
3
4
5
6
1
2
3
4
5
6
故f(x)的最大值不为1,故D错误.
1
2
3
4
5
6
√
解析 由题图可知,A=2,
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
√
1
2
3
4
5
6
解析 由x∈[0,2π],
f(x)在区间[0,2π]上有且仅有4个零点和1个极大值点,
作出y=Acos t的图象如图.
1
2
3
4
5
6
4.[T16补偿](多选)(2021·启东模拟)已知函数f(x)=|sin 2x|+cos 2x,则
A.f(x)=f(x+π)
√
1
2
3
4
5
6
√
解析 对于A,f(x+π)=|sin 2(x+π)|+cos 2(x+π)
=|sin 2x|+cos 2x,正确;
对于B,当sin 2x≥0时,
即2kπ≤2x≤π+2kπ,k∈Z,f(x)=sin 2x+cos 2x
因为2kπ≤2x≤π+2kπ,k∈Z,
1
2
3
4
5
6
当sin 2x<0时,即2kπ+π<2x<2π+2kπ,k∈Z,
f(x)=-sin 2x+cos 2x
因为2kπ+π<2x<2π+2kπ,k∈Z,
1
2
3
4
5
6
所以f(x)的最小值为-1,错误;
对于D,当sin 2x≥0时,即2kπ≤2x≤π+2kπ,k∈Z,
1
2
3
4
5
6
1
2
3
4
5
6
5.[T13补偿](2021·沈阳模拟)关于函数f(x)=2sin x+sin 2x有如下四个命题:
①f(x)的最小正周期为2π;
②f(x)在[0,2π]内有3个极值点;
③f(x)在[0,2π]内有3个零点;
1
2
3
4
5
6
其中所有真命题的序号为________.
①③
解析 由函数y=sin x的最小正周期为2π,函数y=sin 2x的最小正周期为π,
所以函数f(x)=2sin x+sin 2x的最小正周期为两个函数周期的最小公倍数,
所以函数f(x)的最小正周期为2π,所以①正确;
由f′(x)=2cos x+2cos 2x=2cos x+4cos2x-2
=2(2cos x-1)(cos x+1),x∈[0,2π],
因为cos x∈[-1,1],可得cos x+1≥0,
1
2
3
4
5
6
即f(x)在[0,2π]内有2个极值点,所以②不正确;
令f(x)=0,即2sin x+sin 2x=2sin x(1+cos x)=0,
解得sin x=0或cos x=-1,
因为x∈[0,2π],所以x=0,π,2π,
即f(x)在[0,2π]内有3个零点,所以③正确;
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
解析 f(x)=sin(ωx+φ)cos φ+cos(ωx+φ)sin φ=sin(ωx+2φ),
1
2
3
4
5
6
1
2
3
4
5
6
三角函数的图象与性质
第13练
专项典题精练
高考汇编
A.f(x)=|cos 2x| B.f(x)=|sin 2x|
C.f(x)=cos|x| D.f(x)=sin|x|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
C中,函数f(x)=cos|x|=cos x的周期为2π,故C不正确;
在x≥0和x<0时,f(x)均以2π为周期,但在整个定义域上f(x)不是周期函数,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
再将所得曲线上所有点的横坐标扩大到原来的2倍,得到f(x)的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(多选)(2020·新高考全国Ⅰ)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由图象知π
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2018·全国Ⅱ)若f(x)=cos x-sin x在[-a,a]上是减函数,则a的最大值是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f(x)=cos x-sin x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①f(x)在(0,2π)上有且仅有3个极大值点;
②f(x)在(0,2π)上有且仅有2个极小值点;
其中所有正确结论的编号是
A.①④ B.②③ C.①②③ D.①③④
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,根据题意知,xA≤2π
但可能会有3个极小值点,所以②错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
得T=π,所以ω=2,所以f(x)=2cos(2x+φ).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即[f(x)-1]·f(x)>0,可得f(x)>1或f(x)<0,
所以满足题意的最小正整数x为2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 函数f(x)=sin(2x+φ),其中φ∈(0,2π),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·南昌模拟)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,下列有关它的描述正确的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 根据f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(2021·哈尔滨模拟)已知函数f(x)=sin ωx+cos ωx(ω>0),若f(x)在(-π,π)上有且只有3个零点,则ω的取值范围为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若f(x)在(-π,π)上有且只有3个零点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故函数g(x)在该区间上先增后减,故A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.f(x)的周期为π
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D.f(2 020)+f(2 021)=0
√
√
√
则选项A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则选项D正确.
15.(2021·盐城模拟)若函数f(x)=sin(2x+φ)为偶函数,则φ的一个值为___.
(写出一个即可)
解析 依题意知,函数f(x)=sin(2x+φ)为偶函数,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
③f(x)在(0,2π)上有且仅有1个最小值点;
④f(x)的值域为[-1,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以π为函数f(x)的周期.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以函数f(x)在(0,2π)上有且只有1个最小值点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故③正确,④错误.
考情分析
练后疑难精讲
高考必考内容,重点考查三角函数的图象与性质及三角函数图象变换的正用、逆用,多以选择题和填空题的形式考查,也在解答题中出现,难度中等.
一、三角函数的图象及变换
核心提炼
图象变换
(先平移后伸缩)
y=Asin(ωx+φ).
(先伸缩后平移)
y=Asin(ωx+φ).
题号 2 11 13
二、三角函数的解析式
核心提炼
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
(3)求φ,常用的方法有:五点法、特殊点法.
题号 3 4 8 14
三、三角函数的性质
核心提炼
三角函数的常用结论
(1)y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数;
对称轴方程可由ωx+φ=kπ(k∈Z)求得.
(3)y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数.
题号 1 5 6 7 9 10 12 15 16
易错对点精补
1.[T1补偿](多选)(2021·锦州模拟)已知函数f(x)=|cos x|-sin|x|,则下列结论正确的是
A.f(x)是偶函数
B.f(x)是周期函数
1
2
3
4
5
6
D.f(x)的最大值为1
√
√
解析 对于A,f(x)的定义域为R,
且f(-x)=|cos(-x)|-sin|-x|=|cos x|-sin|x|=f(x),所以f(x)为偶函数,故A正确;
对于B,因为y=|cos x|是周期为π的周期函数,y=sin|x|关于y轴对称,不是周期函数,
所以f(x)=|cos x|-sin|x|不是周期函数,故B错误;
1
2
3
4
5
6
1
2
3
4
5
6
故f(x)的最大值不为1,故D错误.
1
2
3
4
5
6
√
解析 由题图可知,A=2,
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
√
1
2
3
4
5
6
解析 由x∈[0,2π],
f(x)在区间[0,2π]上有且仅有4个零点和1个极大值点,
作出y=Acos t的图象如图.
1
2
3
4
5
6
4.[T16补偿](多选)(2021·启东模拟)已知函数f(x)=|sin 2x|+cos 2x,则
A.f(x)=f(x+π)
√
1
2
3
4
5
6
√
解析 对于A,f(x+π)=|sin 2(x+π)|+cos 2(x+π)
=|sin 2x|+cos 2x,正确;
对于B,当sin 2x≥0时,
即2kπ≤2x≤π+2kπ,k∈Z,f(x)=sin 2x+cos 2x
因为2kπ≤2x≤π+2kπ,k∈Z,
1
2
3
4
5
6
当sin 2x<0时,即2kπ+π<2x<2π+2kπ,k∈Z,
f(x)=-sin 2x+cos 2x
因为2kπ+π<2x<2π+2kπ,k∈Z,
1
2
3
4
5
6
所以f(x)的最小值为-1,错误;
对于D,当sin 2x≥0时,即2kπ≤2x≤π+2kπ,k∈Z,
1
2
3
4
5
6
1
2
3
4
5
6
5.[T13补偿](2021·沈阳模拟)关于函数f(x)=2sin x+sin 2x有如下四个命题:
①f(x)的最小正周期为2π;
②f(x)在[0,2π]内有3个极值点;
③f(x)在[0,2π]内有3个零点;
1
2
3
4
5
6
其中所有真命题的序号为________.
①③
解析 由函数y=sin x的最小正周期为2π,函数y=sin 2x的最小正周期为π,
所以函数f(x)=2sin x+sin 2x的最小正周期为两个函数周期的最小公倍数,
所以函数f(x)的最小正周期为2π,所以①正确;
由f′(x)=2cos x+2cos 2x=2cos x+4cos2x-2
=2(2cos x-1)(cos x+1),x∈[0,2π],
因为cos x∈[-1,1],可得cos x+1≥0,
1
2
3
4
5
6
即f(x)在[0,2π]内有2个极值点,所以②不正确;
令f(x)=0,即2sin x+sin 2x=2sin x(1+cos x)=0,
解得sin x=0或cos x=-1,
因为x∈[0,2π],所以x=0,π,2π,
即f(x)在[0,2π]内有3个零点,所以③正确;
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
解析 f(x)=sin(ωx+φ)cos φ+cos(ωx+φ)sin φ=sin(ωx+2φ),
1
2
3
4
5
6
1
2
3
4
5
6
同课章节目录
