第14练 解三角形 课件(共61张PPT)
文档属性
| 名称 | 第14练 解三角形 课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:26:02 | ||
图片预览




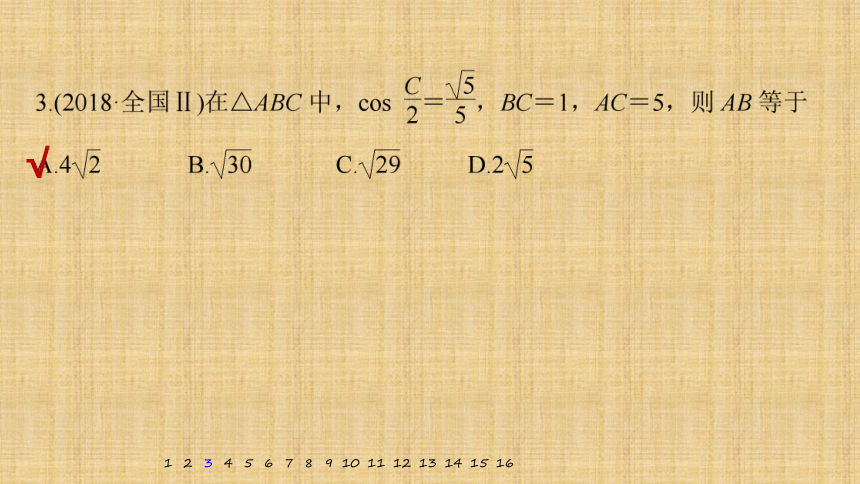





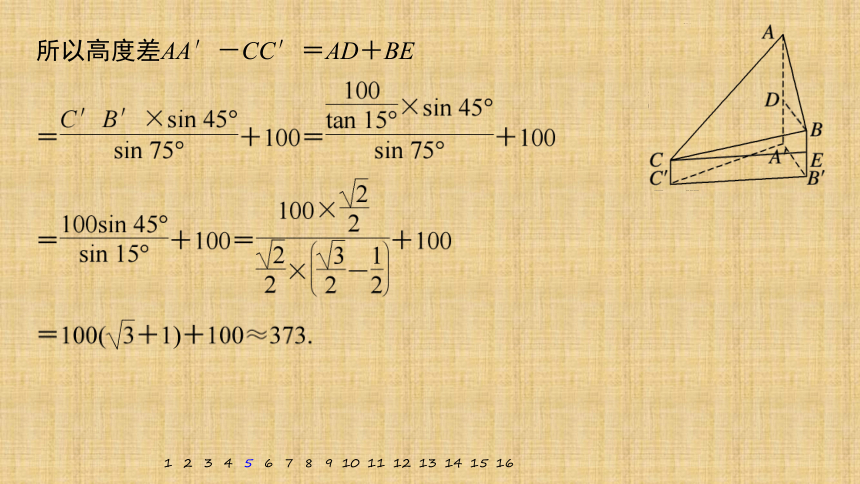
文档简介
(共61张PPT)
解三角形
第14练
专项典题精练
高考汇编
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由余弦定理得AB2=AC2+BC2-2AC·BCcos C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以AB=3,
√
∴sin C=cos C,即tan C=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在△ABC中,由余弦定理,
得AB2=AC2+BC2-2AC·BC·cos C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵asin A-bsin B=4csin C,
∴由正弦定理得a2-b2=4c2,
即a2=4c2+b2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,
C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100,由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为( ≈1.732)
A.346 B.373 C.446 D.473
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图所示,
根据题意过C作CE∥C′B′,交BB′于E,
过B作BD∥A′B′,交AA′于D,
在△A′B′C′中,
又在B点处测得A点的仰角为45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以高度差AA′-CC′=AD+BE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
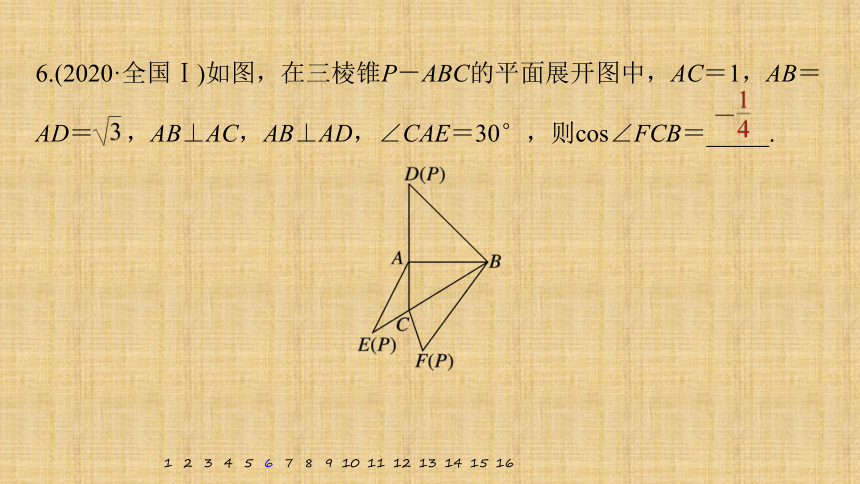
6.(2020·全国Ⅰ)如图,在三棱锥P-ABC的平面展开图中,AC=1,AB=AD= ,AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴CF=CE=1.
∴在△FCB中,由余弦定理得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.(2021·新高考全国Ⅰ)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asin C.
(1)证明:BD=b;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 因为BDsin∠ABC=asin C,
所以由正弦定理得,BD·b=ac,
又b2=ac,所以BD·b=b2,
又b>0,所以BD=b.
(2)若AD=2DC,求cos∠ABC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 如图所示,过点D作DE∥BC交AB于E,
因为AD=2DC,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为∠BED=π-∠ABC,
所以cos∠BED=-cos∠ABC,
化简得3c2+6a2-11ac=0,方程两边同时除以a2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
注:如果选择多个条件分别解答,按第一个解答计分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选条件①.
因此,选条件①时问题中的三角形存在,此时c=1.
选条件②.
选条件③.
因此,选条件③时问题中的三角形不存在.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即sin Acos B=2sin Ccos B-sin Bcos A,
得sin Acos B+cos Asin B=2sin Ccos B,
即sin(A+B)=2sin Ccos B,得sin C=2sin Ccos B,
∵C∈(0,π),∴sin C≠0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又∵a2=b2+c2-2bccos A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·哈尔滨三中模拟)某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面ABO的下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C
的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=30°,A地测得最高点H的仰角为∠OAH=45°,则该仪器的垂直弹射高度CH为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 在△ABC中,由余弦定理可得CB2=AC2+AB2-2AC·ABcos∠BAC,
由题意BA=100,CB=AC-40,∠BAC=60°,
整理可得,20AC=1002-402,解得AC=420,
在Rt△OAC中,∠OAC=30°,
在Rt△OAH中,∠OAH=45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(多选)(2021·重庆育才中学模拟)已知在△ABC中,角A,B,C所对的边分别为a,b,c,且A=60°,b=2,c= +1,则下列说法正确的是
A.C=75°或C=105°
B.B=45°
C.a=
D.该三角形的面积为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由余弦定理得a2=b2+c2-2bccos A
由于0°1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(2021·长郡中学月考)如图,某湖有一半径为100 m的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 m的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足AB=AC,∠BAC=90°.定义:四边形OACB及其内部区域为“直接监测覆盖区域”,设∠AOB=θ.则“直接监测覆盖区域”面积的最大值为____________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 在△OAB中,∵∠AOB=θ,OB=100,OA=200,
∴AB2=OB2+OA2-2OB·OA·cos∠AOB,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4
因为C∈(0,π),所以sin C≠0,
如图,S△ABC=S△ABD+S△ACD,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当c=b,bc=b+c,即c=b=2时等号成立,
所以b+c的最小值为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
注:如果选择多个条件分别解答,按第一个解答计分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 选条件①:
由余弦定理可得a2=b2+c2-bc=(b+c)2-3bc,解得bc=12,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选条件②:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由余弦定理可得a2=b2+c2-2bccos A=b2+c2+bc=(b+c)2-bc,
由已知可得bc=(b+c)2-a2=36,
∴不存在满足条件的△ABC;
选条件③:
由余弦二倍角公式可得2cos2A+3cos A-2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由余弦定理得a2=b2+c2-bc=(b+c)2-3bc,
解得bc=12,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.(2021·盐城模拟)在△ABC中,角A,B,C的对边分别为a,b,c,A=B+3C.
(1)求sin C的取值范围;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由A=B+3C及A+B+C=π,得2B+4C=π,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若c=6b,求sin C的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 因为c=6b,则由正弦定理得sin C=6sin B, ①
所以12sin2C+sin C-6=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
解三角形是高考考查的热点,三角恒等变换单独考查的题目较少,多以解三角形为背景,在用正弦定理、余弦定理的同时,经常应用三角恒等变换进行化简,综合性较强,难度中等.
一、正弦定理、余弦定理
核心提炼
1.正弦定理及其变形
2.余弦定理及其变形
在△ABC中,a2=b2+c2-2bccos A.
题号 1 2 3 4 10 12
二、解三角形在实际生活中的应用
核心提炼
求实际问题的注意事项
(1)选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知,则直接解;若有未知量,则把未知量放在另一确定的三角形中求解.
(2)确定用正弦定理还是余弦定理,如都可用,就选便于计算的定理.
题号 5 11 13
三、正弦定理、余弦定理的综合应用
核心提炼
以三角恒等变换、正弦定理、余弦定理为解题工具,常与三角函数、向量、基本不等式、平面几何等交汇命题.
题号 6 7 8 9 14 15 16
易错对点精补
√
1
2
3
4
5
所以c=3,由余弦定理可得,
a2=b2+c2-2bccos A=13,
1
2
3
4
5
2.[T11补偿](2021·南昌模拟)“欲穷千里目,更上一层楼”出自唐朝诗人王之涣的《登鹳雀楼》,鹳雀楼位于今山西永济市,该楼有三层,前对中条山,下临黄河,传说常有鹳雀在此停留,故有
1
2
3
4
5
此名.下面是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面D点看楼顶点A的仰角为30°,沿直线前进79米到达E点,此时看点C的仰角为45°,若BC=2AC,则楼高AB约为
A.65米 B.74米 C.83米 D.92米
√
解析 设AC的高度为x,
则由已知可得AB=3x,BC=BE=2x,
所以楼高AB≈3×24.7≈74(米).
1
2
3
4
5
1
2
3
4
5
9
解析 由正弦定理可得a2+c2-b2=ac,
因为b=3,所以a2+c2-9=ac,
即(a+c)2-9=3ac,
当且仅当a=c=3时,(a+c)max=6,
所以(a+b+c)max=9,
即△ABC的周长的最大值为9.
1
2
3
4
5
1
2
3
4
5
130
在△BFE中,由正弦定理,可得
1
2
3
4
5
1
2
3
4
5
5.[T16补偿](2021·贵阳模拟)已知△ABC的内角A,B,C所对的边分别为a,b,c,且sin2C-sin2A=sin Bsin C+cos2B-1.
(1)求A;
解 由已知,sin2C-sin2A=sin Bsin C-sin2B,
∴sin2B+sin2C-sin2A=sin Bsin C,
在△ABC中,由正弦定理得b2+c2-a2=bc,
1
2
3
4
5
(2)若△ABC为锐角三角形,且a=1,求△ABC周长的取值范围.
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
解三角形
第14练
专项典题精练
高考汇编
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由余弦定理得AB2=AC2+BC2-2AC·BCcos C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以AB=3,
√
∴sin C=cos C,即tan C=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在△ABC中,由余弦定理,
得AB2=AC2+BC2-2AC·BC·cos C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵asin A-bsin B=4csin C,
∴由正弦定理得a2-b2=4c2,
即a2=4c2+b2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,
C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100,由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为( ≈1.732)
A.346 B.373 C.446 D.473
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图所示,
根据题意过C作CE∥C′B′,交BB′于E,
过B作BD∥A′B′,交AA′于D,
在△A′B′C′中,
又在B点处测得A点的仰角为45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以高度差AA′-CC′=AD+BE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(2020·全国Ⅰ)如图,在三棱锥P-ABC的平面展开图中,AC=1,AB=AD= ,AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴CF=CE=1.
∴在△FCB中,由余弦定理得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.(2021·新高考全国Ⅰ)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asin C.
(1)证明:BD=b;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 因为BDsin∠ABC=asin C,
所以由正弦定理得,BD·b=ac,
又b2=ac,所以BD·b=b2,
又b>0,所以BD=b.
(2)若AD=2DC,求cos∠ABC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 如图所示,过点D作DE∥BC交AB于E,
因为AD=2DC,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为∠BED=π-∠ABC,
所以cos∠BED=-cos∠ABC,
化简得3c2+6a2-11ac=0,方程两边同时除以a2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
注:如果选择多个条件分别解答,按第一个解答计分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选条件①.
因此,选条件①时问题中的三角形存在,此时c=1.
选条件②.
选条件③.
因此,选条件③时问题中的三角形不存在.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即sin Acos B=2sin Ccos B-sin Bcos A,
得sin Acos B+cos Asin B=2sin Ccos B,
即sin(A+B)=2sin Ccos B,得sin C=2sin Ccos B,
∵C∈(0,π),∴sin C≠0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又∵a2=b2+c2-2bccos A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·哈尔滨三中模拟)某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面ABO的下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C
的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=30°,A地测得最高点H的仰角为∠OAH=45°,则该仪器的垂直弹射高度CH为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 在△ABC中,由余弦定理可得CB2=AC2+AB2-2AC·ABcos∠BAC,
由题意BA=100,CB=AC-40,∠BAC=60°,
整理可得,20AC=1002-402,解得AC=420,
在Rt△OAC中,∠OAC=30°,
在Rt△OAH中,∠OAH=45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(多选)(2021·重庆育才中学模拟)已知在△ABC中,角A,B,C所对的边分别为a,b,c,且A=60°,b=2,c= +1,则下列说法正确的是
A.C=75°或C=105°
B.B=45°
C.a=
D.该三角形的面积为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由余弦定理得a2=b2+c2-2bccos A
由于0°
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(2021·长郡中学月考)如图,某湖有一半径为100 m的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 m的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足AB=AC,∠BAC=90°.定义:四边形OACB及其内部区域为“直接监测覆盖区域”,设∠AOB=θ.则“直接监测覆盖区域”面积的最大值为____________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 在△OAB中,∵∠AOB=θ,OB=100,OA=200,
∴AB2=OB2+OA2-2OB·OA·cos∠AOB,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4
因为C∈(0,π),所以sin C≠0,
如图,S△ABC=S△ABD+S△ACD,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当c=b,bc=b+c,即c=b=2时等号成立,
所以b+c的最小值为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
注:如果选择多个条件分别解答,按第一个解答计分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 选条件①:
由余弦定理可得a2=b2+c2-bc=(b+c)2-3bc,解得bc=12,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选条件②:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由余弦定理可得a2=b2+c2-2bccos A=b2+c2+bc=(b+c)2-bc,
由已知可得bc=(b+c)2-a2=36,
∴不存在满足条件的△ABC;
选条件③:
由余弦二倍角公式可得2cos2A+3cos A-2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由余弦定理得a2=b2+c2-bc=(b+c)2-3bc,
解得bc=12,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.(2021·盐城模拟)在△ABC中,角A,B,C的对边分别为a,b,c,A=B+3C.
(1)求sin C的取值范围;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由A=B+3C及A+B+C=π,得2B+4C=π,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若c=6b,求sin C的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 因为c=6b,则由正弦定理得sin C=6sin B, ①
所以12sin2C+sin C-6=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
解三角形是高考考查的热点,三角恒等变换单独考查的题目较少,多以解三角形为背景,在用正弦定理、余弦定理的同时,经常应用三角恒等变换进行化简,综合性较强,难度中等.
一、正弦定理、余弦定理
核心提炼
1.正弦定理及其变形
2.余弦定理及其变形
在△ABC中,a2=b2+c2-2bccos A.
题号 1 2 3 4 10 12
二、解三角形在实际生活中的应用
核心提炼
求实际问题的注意事项
(1)选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知,则直接解;若有未知量,则把未知量放在另一确定的三角形中求解.
(2)确定用正弦定理还是余弦定理,如都可用,就选便于计算的定理.
题号 5 11 13
三、正弦定理、余弦定理的综合应用
核心提炼
以三角恒等变换、正弦定理、余弦定理为解题工具,常与三角函数、向量、基本不等式、平面几何等交汇命题.
题号 6 7 8 9 14 15 16
易错对点精补
√
1
2
3
4
5
所以c=3,由余弦定理可得,
a2=b2+c2-2bccos A=13,
1
2
3
4
5
2.[T11补偿](2021·南昌模拟)“欲穷千里目,更上一层楼”出自唐朝诗人王之涣的《登鹳雀楼》,鹳雀楼位于今山西永济市,该楼有三层,前对中条山,下临黄河,传说常有鹳雀在此停留,故有
1
2
3
4
5
此名.下面是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面D点看楼顶点A的仰角为30°,沿直线前进79米到达E点,此时看点C的仰角为45°,若BC=2AC,则楼高AB约为
A.65米 B.74米 C.83米 D.92米
√
解析 设AC的高度为x,
则由已知可得AB=3x,BC=BE=2x,
所以楼高AB≈3×24.7≈74(米).
1
2
3
4
5
1
2
3
4
5
9
解析 由正弦定理可得a2+c2-b2=ac,
因为b=3,所以a2+c2-9=ac,
即(a+c)2-9=3ac,
当且仅当a=c=3时,(a+c)max=6,
所以(a+b+c)max=9,
即△ABC的周长的最大值为9.
1
2
3
4
5
1
2
3
4
5
130
在△BFE中,由正弦定理,可得
1
2
3
4
5
1
2
3
4
5
5.[T16补偿](2021·贵阳模拟)已知△ABC的内角A,B,C所对的边分别为a,b,c,且sin2C-sin2A=sin Bsin C+cos2B-1.
(1)求A;
解 由已知,sin2C-sin2A=sin Bsin C-sin2B,
∴sin2B+sin2C-sin2A=sin Bsin C,
在△ABC中,由正弦定理得b2+c2-a2=bc,
1
2
3
4
5
(2)若△ABC为锐角三角形,且a=1,求△ABC周长的取值范围.
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
同课章节目录
