第21练 随机变量及其分布 课件(共63张PPT)
文档属性
| 名称 | 第21练 随机变量及其分布 课件(共63张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:42:47 | ||
图片预览







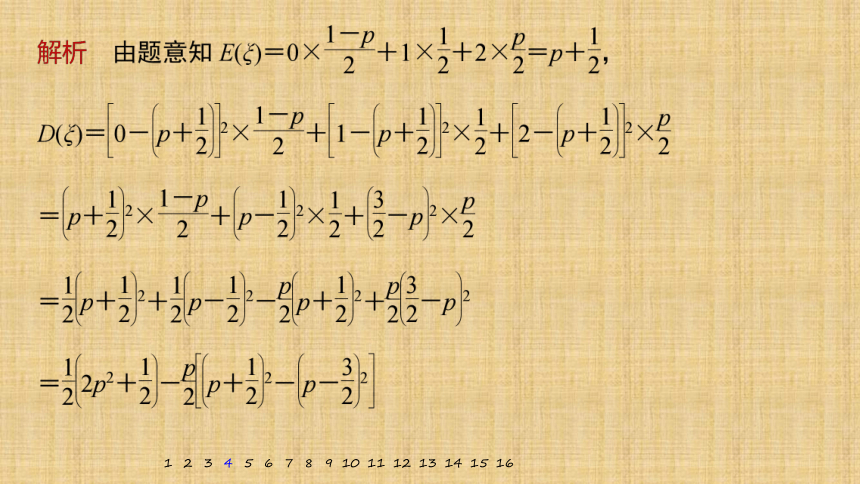




文档简介
(共63张PPT)
随机变量及其分布
第21练
专项典题精练
高考汇编
1.(2018·全国Ⅲ)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,D(X)=2.4,P(X=4)A.0.7 B.0.6
C.0.4 D.0.3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意可知,10位成员中使用移动支付的人数X服从二项分布,
即X~B(10,p),
所以D(X)=10p(1-p)=2.4,
所以p=0.4或0.6.
又因为P(X=4)所以p>0.5,
所以p=0.6.
所以当a在(0,1)内增大时,D(X)先减小后增大.
2.(2019·浙江)设0则当a在(0,1)内增大时,
A.D(X)增大
B.D(X)减小
C.D(X)先增大后减小
D.D(X)先减小后增大
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 a 1
P
√
3.(2021·新高考全国Ⅱ)某物理量的测量结果服从正态分布N(10,σ2),下列结论中不正确的是
A.σ越小,该物理量在一次测量中在(9.9,10.1)的概率越大
B.σ越小,该物理量在一次测量中大于10的概率为0.5
C.σ越小,该物理量在一次测量中小于9.99与大于10.01的概率相等
D.σ越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 对于A,σ2为数据的方差,所以σ越小,数据在μ=10附近越集中,所以测量结果落在(9.9,10.1)内的概率越大,故A正确;
对于B,由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,故B正确;
对于C,由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,故C正确;
对于D,因为该物理量一次测量结果落在(9.9,10.0)的概率与落在(10.2,10.3)的概率不同,所以一次测量结果落在(9.9,10.2)的概率与落在(10,10.3)的概率不同,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(2018·浙江)设01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ξ 0 1 2
P
则当p在(0,1)内增大时,
A.D(ξ)减小 B.D(ξ)增大
C.D(ξ)先减小后增大 D.D(ξ)先增大后减小
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即当p在(0,1)内增大时,D(ξ)先增大后减小.
5.(2017·全国Ⅱ)一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则D(X)=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.96
解析 由题意得X~B(100,0.02),
∴D(X)=100×0.02×(1-0.02)=1.96.
6.(2021·浙江)袋中有4个红球,m个黄球,n个绿球,现从中任取两个球,记取出的红球数为ξ,若取出的两个球都是红球的概率为 ,一红一黄的
概率为 ,则m-n=__,E(ξ)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简得(m+n)2+7(m+n)-60=0,得m+n=5,
解得m=3,故n=2.
所以m-n=1,易知ξ的所有可能取值为0,1,2,
7.(2017·全国Ⅲ)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
解 由题意知,X所有的可能取值为200,300,500,
由表格数据知,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
则X的分布列为
X 200 300 500
P 0.2 0.4 0.4
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的均值达到最大值?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
解 由题意知,这种酸奶一天的需求量至多为500,至少为200,
因此只需考虑200≤n≤500.
当300≤n≤500时,
若最高气温不低于25,则Y=6n-4n=2n;
若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1 200-2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,
因此E(Y)=2n×0.4+(1 200-2n)×0.4+(800-2n)×0.2=640-0.4n.
当200≤n<300时,
若最高气温不低于20,则Y=6n-4n=2n;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,
因此E(Y)=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n.
所以当n=300时,Y的均值达到最大值,最大值为520元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2021·新高考全国Ⅰ)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意得,X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 20 100
P 0.2 0.32 0.48
(2)为使累计得分的均值最大,小明应选择先回答哪类问题?并说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当小明先回答A类问题时,
由(1)可得E(X)=0×0.2+20×0.32+100×0.48=54.4.
当小明先回答B类问题时,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100,
P(Y=0)=1-0.6=0.4,
P(Y=80)=0.6×(1-0.8)=0.12,
P(Y=100)=0.6×0.8=0.48,
所以Y的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Y 0 80 100
P 0.4 0.12 0.48
E(Y)=0×0.4+80×0.12+100×0.48=57.6.
因为57.6>54.4,即E(Y)>E(X),
所以为使累计得分的均值最大,小明应选择先回答B类问题.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.(2021·杭州模拟)已知随机变量ξ满足P(ξ=x)=ax+b(x=-1,0,1),其中a,b∈R.若E(ξ)= ,则D(ξ)等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
解析 根据题意可得分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ξ -1 0 1
P b-a b a+b
10.(2021·常州模拟)俄国著名飞机设计师埃格·西科斯基设计了世界上第一架四引擎飞机和第一种投入生产的直升机,当代著名的“黑鹰”直升机就是由西科斯基公司生产的.1992年,为了远程性和安全性上与美国波音747竞争,欧洲空中客车公司设计并制造了A340,是一种有四台发动机的远程双过道宽体客机,取代只有两台发动机的A310.假设每一架飞机的引擎在飞行中出现故障率为1-p,且各引擎是否有故障是独立的,已知A340飞机至少有3个引擎正常运行,飞机就可成功飞行;A310飞机需要2个引擎全部正常运行,飞机才能成功飞行.若要使A340飞机比A310飞机更安全,则飞机引擎的故障率应控制的范围是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得,飞机引擎正常运行的概率为p,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令-3p4+4p3>p2,即-3p2+4p>1,
11.(多选)(2021·肇庆模拟)已知两种不同型号的电子元件的使用寿命(分别记为X,Y)均服从正态分布, 这两个正态分布密度曲线如图所示,下列选项正确的是
参考数据:若Z~N(μ,σ2),则P(μ-σZ≤μ+2σ)≈0.954 5.
A.P(μ1-σ1≤X≤μ1+2σ1)≈0.818 6
B.P(Y≥μ2)C.P(X≤σ2)D.对于任意的正数t,有P(X≤t)>P(Y≤t)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,由正态分布密度曲线,可知μ1<μ2,所以P(Y≥μ2)对于C,由正态分布密度曲线,可知σ1<σ2,所以P(X≤σ2)>P(X≤σ1),C选项错误;
对于D,对于任意的正数t,由图象知P(X≤t)
表示的面积始终大于P(Y≤t)表示的面积,所
以P(X≤t)>P(Y≤t),D选项正确.
12.(多选)(2021·唐山模拟)下列说法正确的是
A.某投掷类游戏闯关规则是参加游戏者最多投掷5次,只要有一次投中,
即闯关成功,并停止投掷,已知每次投中的概率为 ,则闯关成功的
概率为
B.从10名男生、5名女生中选取4人,则其中至少有一名女生的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
D.若随机变量η~N(2,σ2),且δ=3η+1,则P(η<2)=0.5,E(δ)=6
√
选项B,从10名男生、5名女生中选取4人,
则其中至少有一名女生分为1名女生3名男生、2名女生2名男生、3名女生1名男生和4名都是女生四种情况.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选项D,由随机变量η~N(2,σ2),
则P(η<2)=0.5,E(η)=2,
所以E(δ)=E(3η+1)=3E(η)+1=7,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(2021·嘉兴模拟)甲、乙两人进行5局球赛,甲每局获胜的概率为
,且各局的比赛相互独立,已知甲胜一局的奖金为8元,设甲所获的奖金总额为X元,则甲所获奖金总额的方差D(X)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
60
解析 设甲获胜的局数为Y,
14.(2021·杭州二中模拟)有3个人在一楼进入电梯,楼上共有4层,设每个人在任何一层出电梯的概率相等,并且各层楼无人再进电梯,设电梯中
的人走空时电梯需停的次数为ξ,则E(ξ)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意知,大楼共5层,
则ξi的分布列为
ξi 0 1
P
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(2021·肇庆模拟)为落实中央“坚持五育并举,全面发展素质教育,强化体育锻炼”的指示精神,小明和小亮两名同学每天利用课余时间进行羽毛球比赛.规定每一局比赛中获胜方记2分,失败方记0分,没有平局,
谁先获得10分就获胜,比赛结束.假设每局比赛小明获胜的概率都是
(1)求比赛结束时恰好打了7局的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若现在是小明6∶2的比分领先,记X表示结束比赛还需打的局数,求X的分布列及均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 X的可能取值为2,3,4,5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 2 3 4 5
P
16.(2021·兰州一中模拟)2021年五一期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握五一期间车辆出行的高峰情况,在某高速公路收费点记录了5月1日上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100].例如:10点04分,记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费
点的时刻的平均值(同一组中的数据用该组区间的中点值
代表);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意,得这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为(30×0.005+50×0.015+70×0.020+90×0.010)×20=64,即10点04分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与均值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 结合频率分布直方图和分层抽样的方法可知,抽取的10辆车中,在10:00前通过的车辆数就是位于时间分组中在[20,60)这一区间内的车辆数,
即(0.005+0.015)×20×10=4,
所以X的可能取值为0,1,2,3,4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以X的分布列为
X 0 1 2 3 4
P
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知5月5日全天共有1 000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若T~N(μ,σ2),则P(μ-σ≈0.682 7,P(μ-2σ3σ1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由(1)可得μ=64,
σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+(90-64)2×0.2=324,
所以σ=18.
估计在9:46~10:40这一时间段内通过的车辆数,
也就是46由T~N(μ,σ2),得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以估计在9:46~10:40这一时间段内通过的车辆数为1 000×0.818 6≈
819(辆).
考情分析
练后疑难精讲
高考常考内容,考查离散型随机变量的分布列、均值和方差,以及利用分布列、均值、方差进行决策或分析,多与概率结合考查综合题型,试题阅读量大,常以解答题的形式出现,难度中档偏上.
一、分布列的性质及应用
核心提炼
1.离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
离散型随机变量X的分布列具有两个性质:
(1)pi≥0,i=1,2,…,n;
D(X)=(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-E(X))2·pn=
3.均值、方差的性质
(1)E(aX+b)=aE(X)+b,D(aX+b)=a2D(X).
(2)X~B(n,p),则E(X)=np,D(X)=np(1-p).
(3)X服从两点分布,则E(X)=p,D(X)=p(1-p).
题号 2 4 9
二、随机变量的分布列
核心提炼
1.n次独立重复试验与二项分布
题号 1 5 6 7 8 10 12 13 14 15 16
2.超几何分布
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则X的分布列为P(X=k)= ,k=0,1,2,…,m.
其中n,N,M∈N*,M≤N,n≤N,m=min{n,M}.
三、正态分布
核心提炼
正态曲线的特点
(1)曲线位于x轴上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称,曲线在x=μ处达到峰值
(3)曲线与x轴之间的面积为1.
(4)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
(5)当μ一定时,曲线的形状由σ确定.σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.
题号 3 11
1
2
3
4
5
易错对点精补
1.[T10补偿](2021·新乡模拟)某同学上学的路上有4个红绿灯路口,假如他走到每个红绿灯路口遇到绿灯的概率为 ,则该同学在上学的路上至少遇到2次绿灯的概率为
√
2.[T3补偿](2021·广州模拟)在某次数学测试中,学生成绩ξ服从正态分布(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.6,则任意选取两名学生的成绩,恰有一名学生成绩不高于80的概率为
A.0.16 B.0.24
C.0.32 D.0.48
√
1
2
3
4
5
解析 ∵ξ服从正态分布N(100,σ2),
∴曲线的对称轴是直线x=100,
∵ξ在(80,120)内取值的概率为0.6,
∴ξ在(80,100)内取值的概率为0.3,
∴ξ在(0,80)内取值的概率为0.5-0.3=0.2.
1
2
3
4
5
1
2
3
4
5
3.[T6补偿](2021·绍兴模拟)袋中装有大小相同的1个白球和2个黑球,现分两步从中摸球:第一步从袋中随机摸取2个球后全部放回袋中(若摸得白球则涂成黑球,若摸得黑球则不变色);第二步再从袋中随机摸取2个球,
记第二步所摸取的2个球中白球的个数为ξ,则P(ξ=0)=___,E(ξ)=___.
解析 ξ所有可能结果为1,0,
4.[T13补偿](2021·苏州模拟)在“学习强国”APP中,“争上游”的答题规则为:首局胜利得3分,第二局胜利得2分,失败均得1分.如果甲每局
胜利的概率为 ,且答题相互独立,那么甲作答两局的得分均值为____.
1
2
3
4
5
解析 根据题意,该人参加两局答题活动得分为ξ,
则ξ可取的值为2,3,4,5,
若ξ=2,即该人两局都失败了,
1
2
3
4
5
若ξ=3,即该人第一局失败了,而第二局胜利,
若ξ=4,即该人第一局胜利,而第二局失败,
若ξ=5,即该人两局都胜利了,
1
2
3
4
5
5.[T15补偿](2021·太原模拟)已知6只小白鼠中有且仅有2只患有某种疾病,需要通过化验血液来确定患病的小白鼠.血液化验呈阳性即为患病,阴性为不患病,现将6只小白鼠随机排序并化验血液,每次测1只,且得到前一只小白鼠的血液化验结果之后才化验下一只小白鼠的血液,直到能确定哪两只小白鼠患病为止,并用X表示化验总次数.
(1)在第一只小白鼠验血结果为阳性的条件下,求X=3的概率;
1
2
3
4
5
若A1发生,则需从2只患病小白鼠中选择1只排在第一位,其他位置可随意排,
1
2
3
4
5
若A1与X=3同时发生,则2只患病小白鼠一定排在第一、第三两个位置,
(2)求X的分布列与均值.
1
2
3
4
5
解 随机变量X的可能取值为2,3,4,5,
1
2
3
4
5
故X的分布列是
1
2
3
4
5
X 2 3 4 5
P
随机变量及其分布
第21练
专项典题精练
高考汇编
1.(2018·全国Ⅲ)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,D(X)=2.4,P(X=4)
C.0.4 D.0.3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意可知,10位成员中使用移动支付的人数X服从二项分布,
即X~B(10,p),
所以D(X)=10p(1-p)=2.4,
所以p=0.4或0.6.
又因为P(X=4)
所以p=0.6.
所以当a在(0,1)内增大时,D(X)先减小后增大.
2.(2019·浙江)设0
A.D(X)增大
B.D(X)减小
C.D(X)先增大后减小
D.D(X)先减小后增大
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 a 1
P
√
3.(2021·新高考全国Ⅱ)某物理量的测量结果服从正态分布N(10,σ2),下列结论中不正确的是
A.σ越小,该物理量在一次测量中在(9.9,10.1)的概率越大
B.σ越小,该物理量在一次测量中大于10的概率为0.5
C.σ越小,该物理量在一次测量中小于9.99与大于10.01的概率相等
D.σ越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 对于A,σ2为数据的方差,所以σ越小,数据在μ=10附近越集中,所以测量结果落在(9.9,10.1)内的概率越大,故A正确;
对于B,由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,故B正确;
对于C,由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,故C正确;
对于D,因为该物理量一次测量结果落在(9.9,10.0)的概率与落在(10.2,10.3)的概率不同,所以一次测量结果落在(9.9,10.2)的概率与落在(10,10.3)的概率不同,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(2018·浙江)设0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ξ 0 1 2
P
则当p在(0,1)内增大时,
A.D(ξ)减小 B.D(ξ)增大
C.D(ξ)先减小后增大 D.D(ξ)先增大后减小
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即当p在(0,1)内增大时,D(ξ)先增大后减小.
5.(2017·全国Ⅱ)一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则D(X)=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.96
解析 由题意得X~B(100,0.02),
∴D(X)=100×0.02×(1-0.02)=1.96.
6.(2021·浙江)袋中有4个红球,m个黄球,n个绿球,现从中任取两个球,记取出的红球数为ξ,若取出的两个球都是红球的概率为 ,一红一黄的
概率为 ,则m-n=__,E(ξ)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简得(m+n)2+7(m+n)-60=0,得m+n=5,
解得m=3,故n=2.
所以m-n=1,易知ξ的所有可能取值为0,1,2,
7.(2017·全国Ⅲ)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
解 由题意知,X所有的可能取值为200,300,500,
由表格数据知,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
则X的分布列为
X 200 300 500
P 0.2 0.4 0.4
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的均值达到最大值?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)
天数 2 16 36 25 7 4
解 由题意知,这种酸奶一天的需求量至多为500,至少为200,
因此只需考虑200≤n≤500.
当300≤n≤500时,
若最高气温不低于25,则Y=6n-4n=2n;
若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1 200-2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,
因此E(Y)=2n×0.4+(1 200-2n)×0.4+(800-2n)×0.2=640-0.4n.
当200≤n<300时,
若最高气温不低于20,则Y=6n-4n=2n;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,
因此E(Y)=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n.
所以当n=300时,Y的均值达到最大值,最大值为520元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2021·新高考全国Ⅰ)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意得,X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 20 100
P 0.2 0.32 0.48
(2)为使累计得分的均值最大,小明应选择先回答哪类问题?并说明理由.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当小明先回答A类问题时,
由(1)可得E(X)=0×0.2+20×0.32+100×0.48=54.4.
当小明先回答B类问题时,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100,
P(Y=0)=1-0.6=0.4,
P(Y=80)=0.6×(1-0.8)=0.12,
P(Y=100)=0.6×0.8=0.48,
所以Y的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Y 0 80 100
P 0.4 0.12 0.48
E(Y)=0×0.4+80×0.12+100×0.48=57.6.
因为57.6>54.4,即E(Y)>E(X),
所以为使累计得分的均值最大,小明应选择先回答B类问题.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.(2021·杭州模拟)已知随机变量ξ满足P(ξ=x)=ax+b(x=-1,0,1),其中a,b∈R.若E(ξ)= ,则D(ξ)等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
解析 根据题意可得分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ξ -1 0 1
P b-a b a+b
10.(2021·常州模拟)俄国著名飞机设计师埃格·西科斯基设计了世界上第一架四引擎飞机和第一种投入生产的直升机,当代著名的“黑鹰”直升机就是由西科斯基公司生产的.1992年,为了远程性和安全性上与美国波音747竞争,欧洲空中客车公司设计并制造了A340,是一种有四台发动机的远程双过道宽体客机,取代只有两台发动机的A310.假设每一架飞机的引擎在飞行中出现故障率为1-p,且各引擎是否有故障是独立的,已知A340飞机至少有3个引擎正常运行,飞机就可成功飞行;A310飞机需要2个引擎全部正常运行,飞机才能成功飞行.若要使A340飞机比A310飞机更安全,则飞机引擎的故障率应控制的范围是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得,飞机引擎正常运行的概率为p,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令-3p4+4p3>p2,即-3p2+4p>1,
11.(多选)(2021·肇庆模拟)已知两种不同型号的电子元件的使用寿命(分别记为X,Y)均服从正态分布, 这两个正态分布密度曲线如图所示,下列选项正确的是
参考数据:若Z~N(μ,σ2),则P(μ-σ
A.P(μ1-σ1≤X≤μ1+2σ1)≈0.818 6
B.P(Y≥μ2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,由正态分布密度曲线,可知μ1<μ2,所以P(Y≥μ2)
对于D,对于任意的正数t,由图象知P(X≤t)
表示的面积始终大于P(Y≤t)表示的面积,所
以P(X≤t)>P(Y≤t),D选项正确.
12.(多选)(2021·唐山模拟)下列说法正确的是
A.某投掷类游戏闯关规则是参加游戏者最多投掷5次,只要有一次投中,
即闯关成功,并停止投掷,已知每次投中的概率为 ,则闯关成功的
概率为
B.从10名男生、5名女生中选取4人,则其中至少有一名女生的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
D.若随机变量η~N(2,σ2),且δ=3η+1,则P(η<2)=0.5,E(δ)=6
√
选项B,从10名男生、5名女生中选取4人,
则其中至少有一名女生分为1名女生3名男生、2名女生2名男生、3名女生1名男生和4名都是女生四种情况.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
选项D,由随机变量η~N(2,σ2),
则P(η<2)=0.5,E(η)=2,
所以E(δ)=E(3η+1)=3E(η)+1=7,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(2021·嘉兴模拟)甲、乙两人进行5局球赛,甲每局获胜的概率为
,且各局的比赛相互独立,已知甲胜一局的奖金为8元,设甲所获的奖金总额为X元,则甲所获奖金总额的方差D(X)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
60
解析 设甲获胜的局数为Y,
14.(2021·杭州二中模拟)有3个人在一楼进入电梯,楼上共有4层,设每个人在任何一层出电梯的概率相等,并且各层楼无人再进电梯,设电梯中
的人走空时电梯需停的次数为ξ,则E(ξ)=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意知,大楼共5层,
则ξi的分布列为
ξi 0 1
P
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(2021·肇庆模拟)为落实中央“坚持五育并举,全面发展素质教育,强化体育锻炼”的指示精神,小明和小亮两名同学每天利用课余时间进行羽毛球比赛.规定每一局比赛中获胜方记2分,失败方记0分,没有平局,
谁先获得10分就获胜,比赛结束.假设每局比赛小明获胜的概率都是
(1)求比赛结束时恰好打了7局的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若现在是小明6∶2的比分领先,记X表示结束比赛还需打的局数,求X的分布列及均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 X的可能取值为2,3,4,5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 2 3 4 5
P
16.(2021·兰州一中模拟)2021年五一期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握五一期间车辆出行的高峰情况,在某高速公路收费点记录了5月1日上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100].例如:10点04分,记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费
点的时刻的平均值(同一组中的数据用该组区间的中点值
代表);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意,得这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为(30×0.005+50×0.015+70×0.020+90×0.010)×20=64,即10点04分.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与均值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 结合频率分布直方图和分层抽样的方法可知,抽取的10辆车中,在10:00前通过的车辆数就是位于时间分组中在[20,60)这一区间内的车辆数,
即(0.005+0.015)×20×10=4,
所以X的可能取值为0,1,2,3,4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以X的分布列为
X 0 1 2 3 4
P
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知5月5日全天共有1 000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若T~N(μ,σ2),则P(μ-σ
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由(1)可得μ=64,
σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+(90-64)2×0.2=324,
所以σ=18.
估计在9:46~10:40这一时间段内通过的车辆数,
也就是46
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以估计在9:46~10:40这一时间段内通过的车辆数为1 000×0.818 6≈
819(辆).
考情分析
练后疑难精讲
高考常考内容,考查离散型随机变量的分布列、均值和方差,以及利用分布列、均值、方差进行决策或分析,多与概率结合考查综合题型,试题阅读量大,常以解答题的形式出现,难度中档偏上.
一、分布列的性质及应用
核心提炼
1.离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
离散型随机变量X的分布列具有两个性质:
(1)pi≥0,i=1,2,…,n;
D(X)=(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-E(X))2·pn=
3.均值、方差的性质
(1)E(aX+b)=aE(X)+b,D(aX+b)=a2D(X).
(2)X~B(n,p),则E(X)=np,D(X)=np(1-p).
(3)X服从两点分布,则E(X)=p,D(X)=p(1-p).
题号 2 4 9
二、随机变量的分布列
核心提炼
1.n次独立重复试验与二项分布
题号 1 5 6 7 8 10 12 13 14 15 16
2.超几何分布
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则X的分布列为P(X=k)= ,k=0,1,2,…,m.
其中n,N,M∈N*,M≤N,n≤N,m=min{n,M}.
三、正态分布
核心提炼
正态曲线的特点
(1)曲线位于x轴上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称,曲线在x=μ处达到峰值
(3)曲线与x轴之间的面积为1.
(4)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
(5)当μ一定时,曲线的形状由σ确定.σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.
题号 3 11
1
2
3
4
5
易错对点精补
1.[T10补偿](2021·新乡模拟)某同学上学的路上有4个红绿灯路口,假如他走到每个红绿灯路口遇到绿灯的概率为 ,则该同学在上学的路上至少遇到2次绿灯的概率为
√
2.[T3补偿](2021·广州模拟)在某次数学测试中,学生成绩ξ服从正态分布(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.6,则任意选取两名学生的成绩,恰有一名学生成绩不高于80的概率为
A.0.16 B.0.24
C.0.32 D.0.48
√
1
2
3
4
5
解析 ∵ξ服从正态分布N(100,σ2),
∴曲线的对称轴是直线x=100,
∵ξ在(80,120)内取值的概率为0.6,
∴ξ在(80,100)内取值的概率为0.3,
∴ξ在(0,80)内取值的概率为0.5-0.3=0.2.
1
2
3
4
5
1
2
3
4
5
3.[T6补偿](2021·绍兴模拟)袋中装有大小相同的1个白球和2个黑球,现分两步从中摸球:第一步从袋中随机摸取2个球后全部放回袋中(若摸得白球则涂成黑球,若摸得黑球则不变色);第二步再从袋中随机摸取2个球,
记第二步所摸取的2个球中白球的个数为ξ,则P(ξ=0)=___,E(ξ)=___.
解析 ξ所有可能结果为1,0,
4.[T13补偿](2021·苏州模拟)在“学习强国”APP中,“争上游”的答题规则为:首局胜利得3分,第二局胜利得2分,失败均得1分.如果甲每局
胜利的概率为 ,且答题相互独立,那么甲作答两局的得分均值为____.
1
2
3
4
5
解析 根据题意,该人参加两局答题活动得分为ξ,
则ξ可取的值为2,3,4,5,
若ξ=2,即该人两局都失败了,
1
2
3
4
5
若ξ=3,即该人第一局失败了,而第二局胜利,
若ξ=4,即该人第一局胜利,而第二局失败,
若ξ=5,即该人两局都胜利了,
1
2
3
4
5
5.[T15补偿](2021·太原模拟)已知6只小白鼠中有且仅有2只患有某种疾病,需要通过化验血液来确定患病的小白鼠.血液化验呈阳性即为患病,阴性为不患病,现将6只小白鼠随机排序并化验血液,每次测1只,且得到前一只小白鼠的血液化验结果之后才化验下一只小白鼠的血液,直到能确定哪两只小白鼠患病为止,并用X表示化验总次数.
(1)在第一只小白鼠验血结果为阳性的条件下,求X=3的概率;
1
2
3
4
5
若A1发生,则需从2只患病小白鼠中选择1只排在第一位,其他位置可随意排,
1
2
3
4
5
若A1与X=3同时发生,则2只患病小白鼠一定排在第一、第三两个位置,
(2)求X的分布列与均值.
1
2
3
4
5
解 随机变量X的可能取值为2,3,4,5,
1
2
3
4
5
故X的分布列是
1
2
3
4
5
X 2 3 4 5
P
同课章节目录
