第27练 定点、定值问题 课件(共26张PPT)
文档属性
| 名称 | 第27练 定点、定值问题 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:46:48 | ||
图片预览





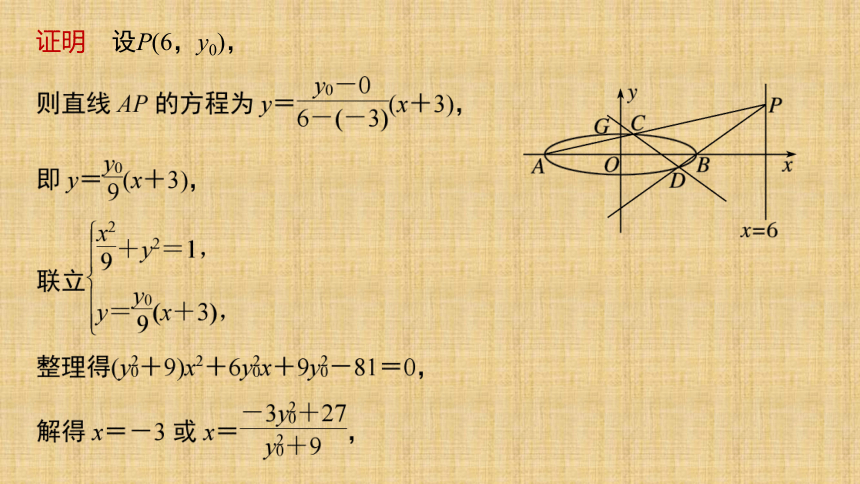

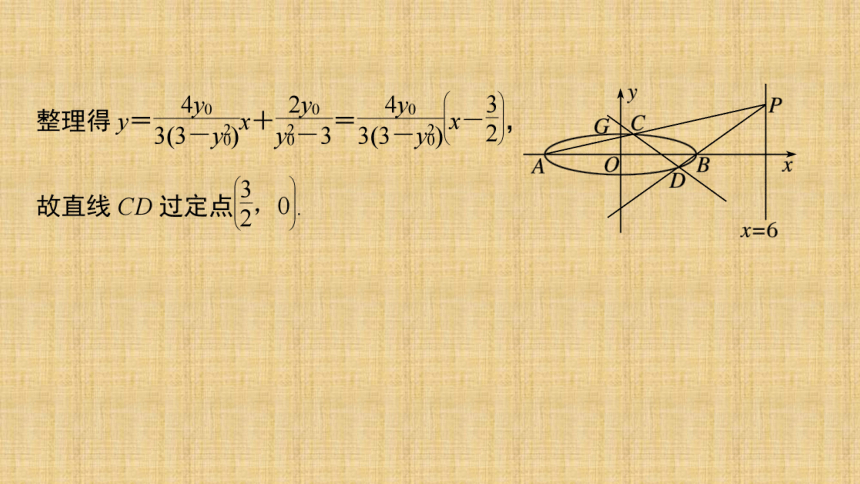

文档简介
(共26张PPT)
定点、定值问题
第27练
考情分析
解析几何是数形结合的典范,是高中数学的主要知识模块,定点和定值问题是高考考查的重点知识,在解答题中一般会综合考查直线、圆、圆锥曲线等,试题难度较大,多次以压轴题出现.
一、定点问题
例1 (2020·全国Ⅰ)已知A,B分别为椭圆E: (a>1)的左、右顶点,
G为E的上顶点, =8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
解 依据题意作图,如图所示.
可得A(-a,0),B(a,0),G(0,1),
解得a=3或a=-3(舍去),
(2)证明:直线CD过定点.
证明 设P(6,y0),
规律方法 求解定点问题常用的方法
(1)“特殊探路,一般证明”,即先通过特殊情况确定定点,再转化为有方向、有目标的一般性证明.
(2)“一般推理,特殊求解”,即先由题设条件得出曲线的方程,再根据参数的任意性得到定点坐标.
(3)求证直线过定点(x0,y0),常利用直线的点斜式方程y-y0=k(x-x0)来证明.
跟踪训练1 (2021·晋中模拟)设椭圆C: (a>b>0),O为原点,点
A(4,0)是x轴上一定点,已知椭圆的长轴长等于|OA|,离心率为
(1)求椭圆C的方程;
所以b2=a2-c2=1,
(2)直线l:y=kx+t与椭圆C交于两个不同点M,N,已知M关于y轴的对称点为M′,N关于原点O的对称点为N′,若M′,N′满足
+ (λ+μ=1),求证:直线l经过定点.
证明 设M(x1,y1),N(x2,y2),
则M′(-x1,y1),N′(-x2,-y2),
可得A,M′,N′三点共线,
所以kAM′=kAN′,即kAN′-kAM′=0,
整理得2kx1x2+(t+4k)(x1+x2)+8t=0. ①
可得(1+4k2)x2+8ktx+4t2-4=0,
整理得t=k,满足Δ>0,
所以直线l的方程为y=kx+k,即y=k(x+1),
即直线l恒过定点(-1,0).
二、定值问题
例2 (2020·新高考全国Ⅰ)已知椭圆C: (a>b>0)的离心率为
,且过点A(2,1).
(1)求C的方程;
解得a2=6,b2=3.
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
证明 设M(x1,y1),N(x2,y2).
若直线MN与x轴不垂直,
得(1+2k2)x2+4kmx+2m2-6=0.
故(x1-2)(x2-2)+(y1-1)(y2-1)=0,
整理得(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0.
整理得(2k+3m+1)(2k+m-1)=0.
因为A(2,1)不在直线MN上,
所以2k+m-1≠0,所以2k+3m+1=0,k≠1.
若直线MN与x轴垂直,可得N(x1,-y1).
得(x1-2)(x1-2)+(y1-1)(-y1-1)=0.
若D与P不重合,则由题设知AP是Rt△ADP的斜边,
规律方法 求圆锥曲线中定值问题常用的方法
(1)引出变量法:其解题流程为
(2)特例法:从特殊入手,求出定值,再证明这个值与变量无关.
(1)求椭圆C的标准方程;
又a2=b2+c2,
解得a=2,b=1,
(2)过定点M(1,0)的直线l与椭圆C相交于A,B两点,已知点 ,设直
线AN,BN的斜率分别为k1,k2,判断k1+k2是否为定值?若是,求出此定值;若不是,说明理由.
解 方法一 ①若AB的斜率不存在,
②若AB的斜率存在,设A(x1,y1),B(x2,y2),
设AB的方程为y=k(x-1),
∴k1+k2=1.
方法二 当直线AB的斜率为0时,A(-2,0),B(2,0),
∴k1+k2=1,
直线AB的斜率不为0时,设直线AB为x=my+1,
设A(x1,y1),B(x2,y2),
∴k1+k2=1.
定点、定值问题
第27练
考情分析
解析几何是数形结合的典范,是高中数学的主要知识模块,定点和定值问题是高考考查的重点知识,在解答题中一般会综合考查直线、圆、圆锥曲线等,试题难度较大,多次以压轴题出现.
一、定点问题
例1 (2020·全国Ⅰ)已知A,B分别为椭圆E: (a>1)的左、右顶点,
G为E的上顶点, =8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
解 依据题意作图,如图所示.
可得A(-a,0),B(a,0),G(0,1),
解得a=3或a=-3(舍去),
(2)证明:直线CD过定点.
证明 设P(6,y0),
规律方法 求解定点问题常用的方法
(1)“特殊探路,一般证明”,即先通过特殊情况确定定点,再转化为有方向、有目标的一般性证明.
(2)“一般推理,特殊求解”,即先由题设条件得出曲线的方程,再根据参数的任意性得到定点坐标.
(3)求证直线过定点(x0,y0),常利用直线的点斜式方程y-y0=k(x-x0)来证明.
跟踪训练1 (2021·晋中模拟)设椭圆C: (a>b>0),O为原点,点
A(4,0)是x轴上一定点,已知椭圆的长轴长等于|OA|,离心率为
(1)求椭圆C的方程;
所以b2=a2-c2=1,
(2)直线l:y=kx+t与椭圆C交于两个不同点M,N,已知M关于y轴的对称点为M′,N关于原点O的对称点为N′,若M′,N′满足
+ (λ+μ=1),求证:直线l经过定点.
证明 设M(x1,y1),N(x2,y2),
则M′(-x1,y1),N′(-x2,-y2),
可得A,M′,N′三点共线,
所以kAM′=kAN′,即kAN′-kAM′=0,
整理得2kx1x2+(t+4k)(x1+x2)+8t=0. ①
可得(1+4k2)x2+8ktx+4t2-4=0,
整理得t=k,满足Δ>0,
所以直线l的方程为y=kx+k,即y=k(x+1),
即直线l恒过定点(-1,0).
二、定值问题
例2 (2020·新高考全国Ⅰ)已知椭圆C: (a>b>0)的离心率为
,且过点A(2,1).
(1)求C的方程;
解得a2=6,b2=3.
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
证明 设M(x1,y1),N(x2,y2).
若直线MN与x轴不垂直,
得(1+2k2)x2+4kmx+2m2-6=0.
故(x1-2)(x2-2)+(y1-1)(y2-1)=0,
整理得(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0.
整理得(2k+3m+1)(2k+m-1)=0.
因为A(2,1)不在直线MN上,
所以2k+m-1≠0,所以2k+3m+1=0,k≠1.
若直线MN与x轴垂直,可得N(x1,-y1).
得(x1-2)(x1-2)+(y1-1)(-y1-1)=0.
若D与P不重合,则由题设知AP是Rt△ADP的斜边,
规律方法 求圆锥曲线中定值问题常用的方法
(1)引出变量法:其解题流程为
(2)特例法:从特殊入手,求出定值,再证明这个值与变量无关.
(1)求椭圆C的标准方程;
又a2=b2+c2,
解得a=2,b=1,
(2)过定点M(1,0)的直线l与椭圆C相交于A,B两点,已知点 ,设直
线AN,BN的斜率分别为k1,k2,判断k1+k2是否为定值?若是,求出此定值;若不是,说明理由.
解 方法一 ①若AB的斜率不存在,
②若AB的斜率存在,设A(x1,y1),B(x2,y2),
设AB的方程为y=k(x-1),
∴k1+k2=1.
方法二 当直线AB的斜率为0时,A(-2,0),B(2,0),
∴k1+k2=1,
直线AB的斜率不为0时,设直线AB为x=my+1,
设A(x1,y1),B(x2,y2),
∴k1+k2=1.
同课章节目录
