第25练 直线与圆锥曲线的位置关系 课件(共77张PPT)
文档属性
| 名称 | 第25练 直线与圆锥曲线的位置关系 课件(共77张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:47:34 | ||
图片预览








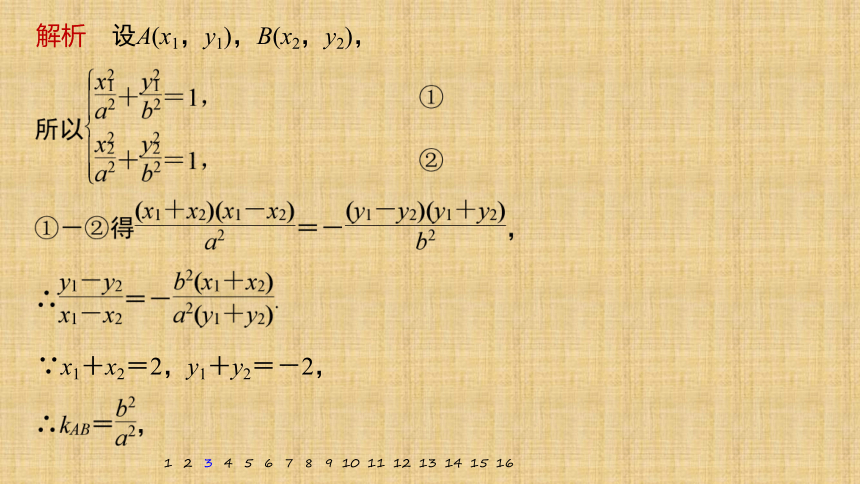
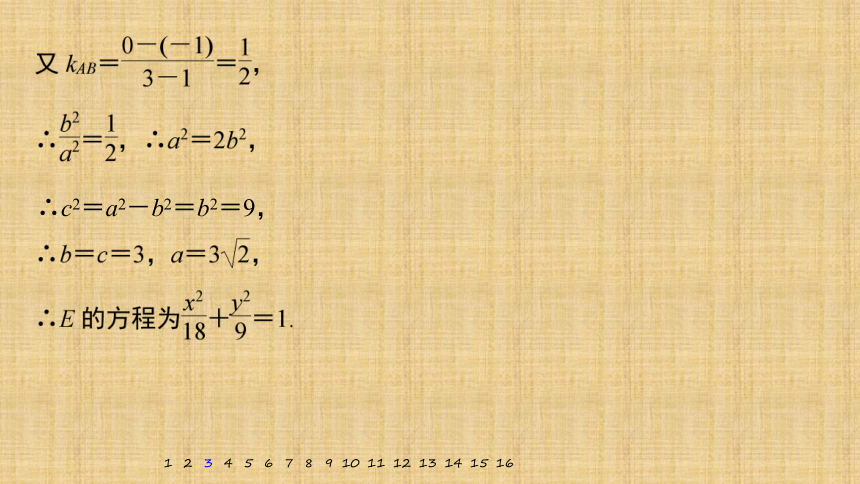


文档简介
(共77张PPT)
直线与圆锥曲线的位置关系
第25练
专项典题精练
高考汇编
1.(2020·全国Ⅰ)设F1,F2是双曲线C: =1的两个焦点,O为坐标原点,
点P在C上且|OP|=2,则△PF1F2的面积为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图,因为|OF1|=|OF2|=|OP|=2,
所以点P在以F1F2为直径的圆上,
故PF1⊥PF2,
则|PF1|2+|PF2|2=(2c)2=16.
由双曲线的定义知||PF1|-|PF2||=2a=2,
所以|PF1|2+|PF2|2-2|PF1||PF2|=4,
所以|PF1||PF2|=6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 由双曲线的方程可知,双曲线的焦点F1,F2在x轴上,
设点P的坐标为(x0,y0),
2.(2014·全国Ⅱ)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(2013·全国Ⅰ)已知椭圆E: (a>b>0)的右焦点为F(3,0),过点F
的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 设A(x1,y1),B(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵x1+x2=2,y1+y2=-2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴c2=a2-b2=b2=9,
4.(2017·全国Ⅰ)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 因为F为y2=4x的焦点,
所以F(1,0).
由题意知直线l1,l2的斜率均存在,且不为0,
设l1的斜率为k,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设A(x1,y1),B(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同理可得|DE|=4(1+k2).
5.(2020·新高考全国Ⅰ)斜率为 的直线过抛物线C:y2=4x的焦点,且与
C交于A,B两点,则|AB|=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,由题意得,抛物线焦点为F(1,0),
得3x2-10x+3=0.
设A(x1,y1),B(x2,y2),
6.(2015·全国Ⅰ)已知F是双曲线C: 的右焦点,P是C的左支上一
点,A .当△APF周长最小时,该三角形的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设左焦点为F1,|PF|-|PF1|=2a=2,
∴|PF|=2+|PF1|,△APF的周长为|AF|+|AP|+|PF|=|AF|+|AP|+2+|PF1|,△APF周长最小即为|AP|+|PF1|最小,
当A,P,F1在一条直线时最小,
7.(2019·全国Ⅰ)已知抛物线C:y2=3x的焦点为F,斜率为 的直线l与C的交点为A,B,与x轴的交点为P.
(1)若|AF|+|BF|=4,求l的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得9x2+12(t-1)x+4t2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以y1+y2=2,从而-3y2+y2=2,
故y2=-1,y1=3,
8.(2020·全国Ⅲ)已知椭圆C: (0分别为C的左、右顶点.
(1)求C的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设P(xP,yP),Q(6,yQ),
根据对称性可设yQ>0,由题意知yP>0.
由已知可得B(5,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为|BP|=|BQ|,所以yP=1.
将yP=1代入C的方程,解得xP=3或xP=-3.
由直线BP的方程得yQ=2或yQ=8,
所以点P,Q的坐标分别为P1(3,1),Q1(6,2);P2(-3,1),Q2(6,8).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知椭圆C: =1,过点P(1,1)的直线l与椭圆C交于A,B两点,若
点P恰为弦AB的中点,则直线l的斜率是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 设A(x1,y1),B(x2,y2),
则x1+x2=2,y1+y2=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由A(a,0),F1(-c,0),F2(c,0),
可得a+c=2(c-a),即c=3a,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 对于A,由椭圆的定义,知2a=|PF1|+|PF2|=6,解得a=3.
∵PF1⊥F1F2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴b2=a2-c2=4,
∴Q在以线段F1F2为直径的圆上,
由c>b知,以线段F1F2为直径的圆与椭圆有4个交点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于D,由题意知点M(-2,1)为弦AB的中点,
设A(x1,y1),B(x2,y2),
∵x1+x2=-4,y1+y2=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即8x-9y+25=0,D正确.
12.(多选)(2021·南京模拟)在平面直角坐标系xOy中,过抛物线x2=2y的焦点的直线l与该抛物线的两个交点为A(x1,y1),B(x2,y2),则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D.经过点B与x轴垂直的直线与直线OA的交点一定在定直线上
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以x1+x2=2k,x1x2=-1,
y1+y2=k(x1+x2)+1=2k2+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故D正确.
13.(2021·深圳模拟)设F为抛物线C:y2=2px(p>0)的焦点,过F作倾斜角为60°的直线交C于A,B两点,若|AF|-|BF|=4,则|AB|=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8
解析 设A(x1,y1),B(x2,y2)(x1>0,x2>0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为p>0,
所以p=3,
14.(2021·宜春模拟)过抛物线C:y2=2px(p>0)的焦点F的直线l与C相交于A,B两点,且A,B两点在准线上的射影分别为M,N,△AFM的面积与△BFN的面积互为倒数,则△MFN的面积为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设|AF|=a,|BF|=b,
由抛物线定义可得|AM|=a,|BN|=b,
且180°-2∠AFM+180°-2∠BFN=180°,
故∠AFM+∠BFN=90°,
故∠MFO+∠NFO=90°,即MF⊥NF.
设∠MAF=θ,
则由余弦定理得|MF|2=2a2(1-cos θ),|NF|2=2b2(1+cos θ),
因为△AFM的面积与△BFN的面积互为倒数,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即a2b2sin2θ=4,
所以△MFN的面积为2.
15.已知曲线C: ,D为直线y= 上的动点,过D作C的两条切线,
切点分别为A,B.
(1)证明:直线AB过定点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为y′=x,所以切线DA的斜率为x1,
整理得2tx1-2y1+1=0.
设B(x2,y2),同理可得2tx2-2y2+1=0.
故直线AB的方程为2tx-2y+1=0.
(2)若以 为圆心的圆与直线AB相切,且切点为线段AB的中点,求
四边形ADBE的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Δ=4t2+4>0,
于是x1+x2=2t,x1x2=-1,
y1+y2=t(x1+x2)+1=2t2+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设d1,d2分别为点D,E到直线AB的距离,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以t+(t2-2)t=0,解得t=0或t=±1.
(1)求椭圆C的标准方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)设过F2的直线l与C交于A,B两点,若|AF1|·|BF1|= ,求|AB|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故直线l的斜率存在,
设直线l:y=k(x-1),A(x1,y1),B(x2,y2).
消去y并整理得(2k2+1)x2-4k2x+2k2-2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得k2=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
直线与圆锥曲线的位置关系是命题的热点,尤其是有关弦长计算及存在性问题,运算量大,能力要求高,突出方程思想、转化化归与分类讨论思想方法的考查,难度为高档.
一、弦长、面积问题
核心提炼
判断方法:通过解直线方程与圆锥曲线方程联立得到的方程组进行判断.
题号 4 6 8 10 14 15 16
二、中点弦问题
核心提炼
解决圆锥曲线“中点弦”问题的方法
1.根与系数的关系法:联立直线与圆锥曲线的方程得到方程组,消元得到一元二次方程后,由根与系数的关系及中点坐标公式求解.
2.点差法:设直线与圆锥曲线的交点(弦的端点)坐标为A(x1,y1),B(x2,y2),将这两点坐标代入圆锥曲线的方程,并对所得两式作差,得到一个与弦AB的中点和直线AB的斜率有关的式子,可以大大减少计算量.
题号 3 9 11
三、圆锥曲线中二级结论的应用
核心提炼
3.抛物线的有关性质:已知抛物线y2=2px(p>0)的焦点为F,直线l过点F且与抛物线交于两点A(x1,y1),B(x2,y2),则
题号 1 2 5 7 12 13
(2)以AB为直径的圆与抛物线的准线相切.
1
2
3
4
5
易错对点精补
1.[T3补偿]已知椭圆M: (a>b>0),过M的右焦点F(3,0)作直线交
椭圆于A,B两点,若AB中点坐标为(2,1),则椭圆M的方程为
√
解析 设A(x1,y1),B(x2,y2),AB的中点P(2,1),
1
2
3
4
5
1
2
3
4
5
2.[T6补偿]已知双曲线C: 的左焦点为F,点M在双曲线C的右支
上,A(0,4),当△MAF的周长最小时,△MAF的面积为
A.12 B.8 C.6 D.4
√
1
2
3
4
5
解析 如图所示,设双曲线C的右焦点为F′,
1
2
3
4
5
所以F(-4,0),F′(4,0),
即当M在M′处时,△MAF的周长最小,
此时直线AF′的方程为y=-x+4,
1
2
3
4
5
整理得y-1=0,则yM′=1,
1
2
3
4
5
1
2
3
4
5
设P(x1,y1),Q(x2,y2),
因为P,Q在椭圆上,
1
2
3
4
5
4.[T14补偿](2021·苏州模拟)已知抛物线C:y2=2px(p>0)的焦点为F,点P是抛物线C上一点,以F为圆心,半径为p的圆与PF交于点Q,过点P作圆
F的切线,切点为A,若|PA|= ,且△OPQ的面积为 ,则p=____.
1
2
3
4
5
2
因为|FQ|=p,
所以Q是线段PF的中点,
1
2
3
4
5
1
2
3
4
5
(1)求椭圆的标准方程;
1
2
3
4
5
又∵a2=b2+c2,
∴a2=6,b2=2,
(2)过椭圆右焦点F的动直线l交椭圆于A,B两点,P为直线x=3上的一点,是否存在直线l与点P,使得△ABP恰好为等边三角形,若存在,求出△ABP的面积;若不存在,请说明理由.
1
2
3
4
5
解 当直线l的斜率不存在时,等边△ABP不存在,故直线l的斜率存在.
设直线l:y=k(x-2),
联立椭圆方程整理得(3k2+1)x2-12k2x+12k2-6=0,
记A(x1,y1),B(x2,y2),
1
2
3
4
5
记AB中点为M(x0,y0),
1
2
3
4
5
∴k=±1,经检验k=±1均符合题意.
直线与圆锥曲线的位置关系
第25练
专项典题精练
高考汇编
1.(2020·全国Ⅰ)设F1,F2是双曲线C: =1的两个焦点,O为坐标原点,
点P在C上且|OP|=2,则△PF1F2的面积为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图,因为|OF1|=|OF2|=|OP|=2,
所以点P在以F1F2为直径的圆上,
故PF1⊥PF2,
则|PF1|2+|PF2|2=(2c)2=16.
由双曲线的定义知||PF1|-|PF2||=2a=2,
所以|PF1|2+|PF2|2-2|PF1||PF2|=4,
所以|PF1||PF2|=6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 由双曲线的方程可知,双曲线的焦点F1,F2在x轴上,
设点P的坐标为(x0,y0),
2.(2014·全国Ⅱ)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(2013·全国Ⅰ)已知椭圆E: (a>b>0)的右焦点为F(3,0),过点F
的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 设A(x1,y1),B(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵x1+x2=2,y1+y2=-2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴c2=a2-b2=b2=9,
4.(2017·全国Ⅰ)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 因为F为y2=4x的焦点,
所以F(1,0).
由题意知直线l1,l2的斜率均存在,且不为0,
设l1的斜率为k,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设A(x1,y1),B(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同理可得|DE|=4(1+k2).
5.(2020·新高考全国Ⅰ)斜率为 的直线过抛物线C:y2=4x的焦点,且与
C交于A,B两点,则|AB|=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,由题意得,抛物线焦点为F(1,0),
得3x2-10x+3=0.
设A(x1,y1),B(x2,y2),
6.(2015·全国Ⅰ)已知F是双曲线C: 的右焦点,P是C的左支上一
点,A .当△APF周长最小时,该三角形的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设左焦点为F1,|PF|-|PF1|=2a=2,
∴|PF|=2+|PF1|,△APF的周长为|AF|+|AP|+|PF|=|AF|+|AP|+2+|PF1|,△APF周长最小即为|AP|+|PF1|最小,
当A,P,F1在一条直线时最小,
7.(2019·全国Ⅰ)已知抛物线C:y2=3x的焦点为F,斜率为 的直线l与C的交点为A,B,与x轴的交点为P.
(1)若|AF|+|BF|=4,求l的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得9x2+12(t-1)x+4t2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以y1+y2=2,从而-3y2+y2=2,
故y2=-1,y1=3,
8.(2020·全国Ⅲ)已知椭圆C: (0
(1)求C的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设P(xP,yP),Q(6,yQ),
根据对称性可设yQ>0,由题意知yP>0.
由已知可得B(5,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为|BP|=|BQ|,所以yP=1.
将yP=1代入C的方程,解得xP=3或xP=-3.
由直线BP的方程得yQ=2或yQ=8,
所以点P,Q的坐标分别为P1(3,1),Q1(6,2);P2(-3,1),Q2(6,8).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知椭圆C: =1,过点P(1,1)的直线l与椭圆C交于A,B两点,若
点P恰为弦AB的中点,则直线l的斜率是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 设A(x1,y1),B(x2,y2),
则x1+x2=2,y1+y2=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由A(a,0),F1(-c,0),F2(c,0),
可得a+c=2(c-a),即c=3a,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 对于A,由椭圆的定义,知2a=|PF1|+|PF2|=6,解得a=3.
∵PF1⊥F1F2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴b2=a2-c2=4,
∴Q在以线段F1F2为直径的圆上,
由c>b知,以线段F1F2为直径的圆与椭圆有4个交点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于D,由题意知点M(-2,1)为弦AB的中点,
设A(x1,y1),B(x2,y2),
∵x1+x2=-4,y1+y2=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即8x-9y+25=0,D正确.
12.(多选)(2021·南京模拟)在平面直角坐标系xOy中,过抛物线x2=2y的焦点的直线l与该抛物线的两个交点为A(x1,y1),B(x2,y2),则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D.经过点B与x轴垂直的直线与直线OA的交点一定在定直线上
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以x1+x2=2k,x1x2=-1,
y1+y2=k(x1+x2)+1=2k2+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故D正确.
13.(2021·深圳模拟)设F为抛物线C:y2=2px(p>0)的焦点,过F作倾斜角为60°的直线交C于A,B两点,若|AF|-|BF|=4,则|AB|=___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8
解析 设A(x1,y1),B(x2,y2)(x1>0,x2>0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为p>0,
所以p=3,
14.(2021·宜春模拟)过抛物线C:y2=2px(p>0)的焦点F的直线l与C相交于A,B两点,且A,B两点在准线上的射影分别为M,N,△AFM的面积与△BFN的面积互为倒数,则△MFN的面积为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设|AF|=a,|BF|=b,
由抛物线定义可得|AM|=a,|BN|=b,
且180°-2∠AFM+180°-2∠BFN=180°,
故∠AFM+∠BFN=90°,
故∠MFO+∠NFO=90°,即MF⊥NF.
设∠MAF=θ,
则由余弦定理得|MF|2=2a2(1-cos θ),|NF|2=2b2(1+cos θ),
因为△AFM的面积与△BFN的面积互为倒数,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即a2b2sin2θ=4,
所以△MFN的面积为2.
15.已知曲线C: ,D为直线y= 上的动点,过D作C的两条切线,
切点分别为A,B.
(1)证明:直线AB过定点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为y′=x,所以切线DA的斜率为x1,
整理得2tx1-2y1+1=0.
设B(x2,y2),同理可得2tx2-2y2+1=0.
故直线AB的方程为2tx-2y+1=0.
(2)若以 为圆心的圆与直线AB相切,且切点为线段AB的中点,求
四边形ADBE的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Δ=4t2+4>0,
于是x1+x2=2t,x1x2=-1,
y1+y2=t(x1+x2)+1=2t2+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设d1,d2分别为点D,E到直线AB的距离,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以t+(t2-2)t=0,解得t=0或t=±1.
(1)求椭圆C的标准方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)设过F2的直线l与C交于A,B两点,若|AF1|·|BF1|= ,求|AB|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故直线l的斜率存在,
设直线l:y=k(x-1),A(x1,y1),B(x2,y2).
消去y并整理得(2k2+1)x2-4k2x+2k2-2=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得k2=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
考情分析
练后疑难精讲
直线与圆锥曲线的位置关系是命题的热点,尤其是有关弦长计算及存在性问题,运算量大,能力要求高,突出方程思想、转化化归与分类讨论思想方法的考查,难度为高档.
一、弦长、面积问题
核心提炼
判断方法:通过解直线方程与圆锥曲线方程联立得到的方程组进行判断.
题号 4 6 8 10 14 15 16
二、中点弦问题
核心提炼
解决圆锥曲线“中点弦”问题的方法
1.根与系数的关系法:联立直线与圆锥曲线的方程得到方程组,消元得到一元二次方程后,由根与系数的关系及中点坐标公式求解.
2.点差法:设直线与圆锥曲线的交点(弦的端点)坐标为A(x1,y1),B(x2,y2),将这两点坐标代入圆锥曲线的方程,并对所得两式作差,得到一个与弦AB的中点和直线AB的斜率有关的式子,可以大大减少计算量.
题号 3 9 11
三、圆锥曲线中二级结论的应用
核心提炼
3.抛物线的有关性质:已知抛物线y2=2px(p>0)的焦点为F,直线l过点F且与抛物线交于两点A(x1,y1),B(x2,y2),则
题号 1 2 5 7 12 13
(2)以AB为直径的圆与抛物线的准线相切.
1
2
3
4
5
易错对点精补
1.[T3补偿]已知椭圆M: (a>b>0),过M的右焦点F(3,0)作直线交
椭圆于A,B两点,若AB中点坐标为(2,1),则椭圆M的方程为
√
解析 设A(x1,y1),B(x2,y2),AB的中点P(2,1),
1
2
3
4
5
1
2
3
4
5
2.[T6补偿]已知双曲线C: 的左焦点为F,点M在双曲线C的右支
上,A(0,4),当△MAF的周长最小时,△MAF的面积为
A.12 B.8 C.6 D.4
√
1
2
3
4
5
解析 如图所示,设双曲线C的右焦点为F′,
1
2
3
4
5
所以F(-4,0),F′(4,0),
即当M在M′处时,△MAF的周长最小,
此时直线AF′的方程为y=-x+4,
1
2
3
4
5
整理得y-1=0,则yM′=1,
1
2
3
4
5
1
2
3
4
5
设P(x1,y1),Q(x2,y2),
因为P,Q在椭圆上,
1
2
3
4
5
4.[T14补偿](2021·苏州模拟)已知抛物线C:y2=2px(p>0)的焦点为F,点P是抛物线C上一点,以F为圆心,半径为p的圆与PF交于点Q,过点P作圆
F的切线,切点为A,若|PA|= ,且△OPQ的面积为 ,则p=____.
1
2
3
4
5
2
因为|FQ|=p,
所以Q是线段PF的中点,
1
2
3
4
5
1
2
3
4
5
(1)求椭圆的标准方程;
1
2
3
4
5
又∵a2=b2+c2,
∴a2=6,b2=2,
(2)过椭圆右焦点F的动直线l交椭圆于A,B两点,P为直线x=3上的一点,是否存在直线l与点P,使得△ABP恰好为等边三角形,若存在,求出△ABP的面积;若不存在,请说明理由.
1
2
3
4
5
解 当直线l的斜率不存在时,等边△ABP不存在,故直线l的斜率存在.
设直线l:y=k(x-2),
联立椭圆方程整理得(3k2+1)x2-12k2x+12k2-6=0,
记A(x1,y1),B(x2,y2),
1
2
3
4
5
记AB中点为M(x0,y0),
1
2
3
4
5
∴k=±1,经检验k=±1均符合题意.
同课章节目录
