第31练 分类讨论思想 课件(共64张PPT)
文档属性
| 名称 | 第31练 分类讨论思想 课件(共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 17:00:37 | ||
图片预览











文档简介
(共64张PPT)
分类讨论思想
第31练
专项典题精练
高考汇编
1.(2020·浙江)已知空间中不过同一点的三条直线l,m,n,“l,m,n共面”是“l,m,n两两相交”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,直线l,m,n不过同一点,且l,m,n共面有三种情况:
①同一平面内三线平行;
②两平行线与另一线相交;
③三线两两相交.
因此,“l,m,n两两相交”是“l,m,n共面”的一种情况,
即“l,m,n共面”是“l,m,n两两相交”的必要不充分条件.
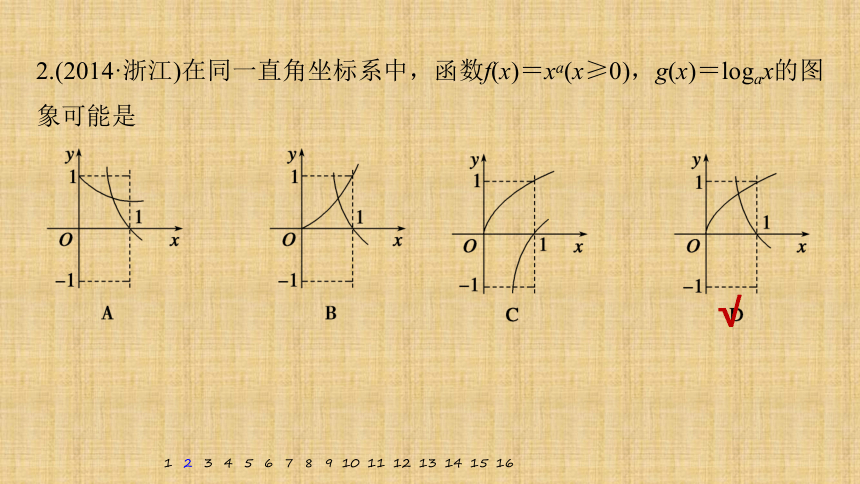
2.(2014·浙江)在同一直角坐标系中,函数f(x)=xa(x≥0),g(x)=logax的图象可能是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 当a>1时,y=xa与y=logax均为增函数,但y=xa递增较快,排除C;
当0方法二 幂函数f(x)=xa的图象不过(0,1)点,排除A;
B项中由对数函数f(x)=logax的图象知0C项中由对数函数f(x)=logax的图象知a>1,而此时幂函数f(x)=xa的图象应是增长越来越快的变化趋势,故C错.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(2015·山东)设函数f(x)= 则满足f(f(a))=2f(a)的a的取值范围是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由f(f(a))=2f(a)得,f(a)≥1.
当a<1时,有3a-1≥1,
当a≥1时,有2a≥1,∴a≥0,∴a≥1.
4.(2017·全国Ⅰ)设A,B是椭圆C: 长轴的两个端点.若C上存在点
M满足∠AMB=120°,则m的取值范围是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 设焦点在x轴上,点M(x,y).
过点M作x轴的垂线,交x轴于点N,
则N(x,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于焦点在y轴上的情况,同理亦可得m≥9.
则m的取值范围是(0,1]∪[9,+∞).
方法二 当0要使C上存在点M满足∠AMB=120°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得0当m>3时,焦点在y轴上,
要使C上存在点M满足∠AMB=120°,
故m的取值范围为(0,1]∪[9,+∞).
5.(2018·全国Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.已知bsin C
+csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 △ABC的内角A,B,C的对边分别为a,b,c,
bsin C+csin B=4asin Bsin C,
利用正弦定理可得sin Bsin C+sin Csin B=4sin Asin Bsin C,
由于0所以sin Bsin C≠0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于b2+c2-a2=8,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 ∵bsin C+csin B=4asin Bsin C,
∴由正弦定理得sin Bsin C+sin Csin B=4sin Asin Bsin C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(2014·福建)函数f(x)= 的零点个数是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
所以在(-∞,0]上有一个零点.
所以f(x)在(0,+∞)上单调递增.
又因为f(2)=-2+ln 2<0,f(3)=ln 3>0,f(2)·f(3)<0,
所以f(x)在(2,3)内有一个零点.
综上,函数f(x)的零点个数为2.
7.(2017·全国Ⅰ)已知函数f(x)=ex(ex-a)-a2x.
(1)讨论f(x)的单调性;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 函数f(x)的定义域为(-∞,+∞),
f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).
①若a=0,则f(x)=e2x在(-∞,+∞)上单调递增.
②若a>0,则由f′(x)=0,得x=ln a.
当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
故f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若f(x)≥0,求a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ①若a=0,则f(x)=e2x,所以f(x)>0,符合题意.
②若a>0,则由(1)知,当x=ln a时,f(x)取得最小值,
最小值为f(ln a)=-a2ln a,
从而当且仅当-a2ln a≥0,即01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即 ≤a<0时,f(x)≥0.
综上,a的取值范围是[ ,1].
8.(2018·全国Ⅰ)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线BM的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当l与x轴垂直时,l的方程为x=2,可得点M的坐标为(2,2)或(2,-2).
即x-2y+2=0或x+2y+2=0.
(2)证明:∠ABM=∠ABN.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 当l与x轴垂直时,AB为MN的垂直平分线,
所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为y=k(x-2)(k≠0),
M(x1,y1),N(x2,y2),则x1>0,x2>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以kBM+kBN=0,可知BM,BN的倾斜角互补,
所以∠ABM=∠ABN.
综上,∠ABM=∠ABN.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 由m是1和9的等比中项,可得m=±3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
该曲线为焦点在y轴上的椭圆,
该曲线为焦点在x轴上的双曲线,
10.(2021·遂宁模拟)已知过点(0,2)的直线l与圆心为C的圆(x-2)2+(y-1)2=10相交于A,B两点,若CA⊥CB,则直线l的方程为
A.2x-y+2=0
B.2x-y+2=0或2x+y-2=0
C.x=0
D.x=0或2x+y-2=0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以△ABC是以∠ACB为直角的等腰直角三角形,
若直线l的斜率不存在,则直线l的方程为x=0,
此时点C到直线l的距离为2,不符合题意;
若直线l的斜率存在,设直线l的方程为y=kx+2,即kx-y+2=0,
整理得(k-2)2=0,解得k=2,
所以直线l的方程为y=2x+2,即2x-y+2=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.若不等式(a-2)x2+2(a-2)x-4<0对任意实数x均成立,则实数a的取值范围是
A.(-2,2) B.[-2,2]
C.(2,+∞) D.(-2,2]
√
解析 当a-2=0,即a=2时,此时-4<0恒成立,满足条件;
当a-2≠0时,因为(a-2)x2+2(a-2)x-4<0对任意实数x都成立,
解得a∈(-2,2),综上可知,a∈(-2,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由已知得f′(x)=a(sin x+xcos x),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又函数图象是连续不断的,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又函数图象是连续不断的,
13.已知集合A={x|-2≤x≤7},B={x|m+11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(-∞,4]
解析 当B= 时,有m+1≥2m-1,则m≤2;
当B≠ 时,若B A,如图.
综上,m的取值范围为(-∞,4].
14.(2021·杭州模拟)一排有11个座位,现安排2人就座,规定中间的3个座位不能坐,且2人不相邻,则不同排法的种数是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
44
解析 根据两人在三个空位同侧与异侧进行分类,
即共6+6+32=44(种).
15.(2021·柳州模拟)已知数列{an}的前n项和是Sn,且满足Sn=2an-1,n∈N*.
(1)求数列{an}的通项公式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 依题意得,当n=1时,有S1=2a1-1,
又S1=a1,故a1=1,
又Sn=2an-1, ①
当n≥2时,有Sn-1=2an-1-1, ②
①-②得Sn-Sn-1=an=2an-2an-1,
化简得an=2an-1,
∴{an}是以1为首项,2为公比的等比数列,
∴an=2n-1.
(2)若bn=2n-1,且数列{cn}由a1,b1,a2,b2,a3,b3,…,an,bn,…组成,求{cn}的前n项和Tn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当n为偶数时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tn=a1+b1+a2+b2+a3+b3+…+
=a1+a2+a3+…+ +b1+b2+b3+…+
=
=
=
当n为奇数时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tn=a1+b1+a2+b2+a3+b3+…+
=a1+a2+a3+…+ +b1+b2+b3+…+
=
=
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=
∴Tn=
16.(2021·丰台区模拟)已知椭圆C: ,过点(-1,0)的直线l交椭圆C于点A,B.
(1)当直线l与x轴垂直时,求|AB|;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当直线l与x轴垂直时,其方程为x=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①当直线l斜率存在时,
设直线l的方程为y=k(x+1),A(x1,y1),B(x2,y2),
得(1+3k2)x2+6k2x+3k2-3=0.显然Δ>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=x1x2-m(x1+x2)+m2+k2(x1+1)(x2+1)
=x1x2-m(x1+x2)+m2+k2x1x2+k2(x1+x2)+k2
=(k2-m)(x1+x2)+(k2+1)x1x2+k2+m2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②当直线l与x轴垂直时,
考情分析
练后疑难精讲
分类讨论思想是当问题的对象不能进行统一研究时,就需要对研究的对象按某个标准进行分类,然后对每一类分别研究,给出每一类的结论,最终综合各类结果得到整个问题的解答.实质上分类讨论就是“化整为零,各个击破,再集零为整”的数学思想.
一、由概念、法则、公式、性质引起的分类讨论
核心提炼
解决由概念、法则、公式引起的分类讨论问题的步骤
第一步:确定需分类的目标与对象.即确定需要分类的目标,一般把需要用到公式、定理解决问题的对象作为分类目标.
第二步:根据公式、定理确定分类标准.运用公式、定理对分类对象进行区分.
第三步:分类解决“分目标”问题.对分类出来的“分目标”分别进行处理.
第四步:汇总“分目标”.将“分目标”问题进行汇总,并作进一步处理.
题号 1 5 6 10 13 14 15
二、由参数变化引起的分类讨论
核心提炼
含有参数的分类讨论问题主要包括:(1)含有参数的不等式的求解;(2)含有参数的方程的求解;(3)函数解析式中含参数的最值与单调性问题;(4)二元二次方程表示曲线类型的判定等.求解这类问题的一般思路是:结合参数的意义及参数对结果的影响进行分类讨论.讨论时,应全面分析参数变化引起结论的变化情况,参数有几何意义时还要考虑适当地运用数形结合思想.
题号 3 4 7 11 12
三、由图形位置或形状引起的分类讨论
核心提炼
1.一般由图形的位置或形状变动引发的讨论包括:二次函数对称轴位置的变动;函数问题中区间的变动;函数图象形状的变动;直线由斜率引起的位置变动;圆锥曲线由焦点引起的位置变动或由离心率引起的形状变动;立体几何中点、线、面的位置变动等.
2.圆锥曲线形状不确定时,常按椭圆、双曲线来分类讨论,求圆锥曲线的方程时,常按焦点的位置不同来分类讨论.
3.相关计算中,涉及图形问题时,也常按图形的位置不同、大小差异等来分类讨论.
题号 2 8 9 16
1
2
3
4
5
易错对点精补
1.[T1补偿](2021·房山区模拟)“a2=1”是“直线x+ay=1与ax+y=1平行”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
1
2
3
4
5
解析 因为直线x+ay=1与ax+y=1平行,
解得a=±1;
而当a=1时,直线x+ay=1为x+y=1,
同时ax+y=1为x+y=1,两直线重合不满足题意;
当a=-1时,x-y=1与-x+y=1平行,满足题意;
故a=-1,根据小范围推大范围可得,
a2=1是a=-1的必要不充分条件.
1
2
3
4
5
√
1
2
3
4
5
1
2
3
4
5
3.[T6补偿]已知λ∈R,函数f(x)= 当λ=2时,不等式f(x)<0
的解集是_____.若函数f(x)恰有2个零点,则λ的取值范围是_______________.
(1,4)
(1,3]∪(4,+∞)
1
2
3
4
5
所以2≤x<4或1即1当λ>4时,f(x)=x-4>0,
此时令f(x)=x2-4x+3=0,解得x=1或x=3,
即在(-∞,λ)上有两个零点,满足题意;
当λ≤4时,令f(x)=x-4=0,解得x=4,
由f(x)=x2-4x+3在(-∞,λ)上只能有一个零点得1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
4.[T12补偿]若函数f(x)=mx2-x+ln x存在单调递减区间,则实数m的取
值范围是__________.
1
2
3
4
5
1
2
3
4
5
即2mx2-x+1<0在(0,+∞)上有解.
当m≤0时显然成立;当m>0时,
5.[T7补偿](2021·洛阳模拟)已知函数f(x)=ax-x2-ln x(a∈R).
(1)求函数f(x)的单调区间;
1
2
3
4
5
1
2
3
4
5
由f′(x)>0得x1由f′(x)<0得0x2,
1
2
3
4
5
函数f(x)的单调递减区间为(0,+∞),无单调递增区间;
(2)若函数f(x)存在极值,且这些极值的和大于5+ln 2,求实数a的取值范围.
1
2
3
4
5
1
2
3
4
5
此时方程2x2-ax+1=0有两个不相等的正根x1,x2,
=a(x1+x2)-[(x1+x2)2-2x1x2]-ln(x1x2)
1
2
3
4
5
∴a的取值范围是(4,+∞).
分类讨论思想
第31练
专项典题精练
高考汇编
1.(2020·浙江)已知空间中不过同一点的三条直线l,m,n,“l,m,n共面”是“l,m,n两两相交”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,直线l,m,n不过同一点,且l,m,n共面有三种情况:
①同一平面内三线平行;
②两平行线与另一线相交;
③三线两两相交.
因此,“l,m,n两两相交”是“l,m,n共面”的一种情况,
即“l,m,n共面”是“l,m,n两两相交”的必要不充分条件.
2.(2014·浙江)在同一直角坐标系中,函数f(x)=xa(x≥0),g(x)=logax的图象可能是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 当a>1时,y=xa与y=logax均为增函数,但y=xa递增较快,排除C;
当0
B项中由对数函数f(x)=logax的图象知0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(2015·山东)设函数f(x)= 则满足f(f(a))=2f(a)的a的取值范围是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由f(f(a))=2f(a)得,f(a)≥1.
当a<1时,有3a-1≥1,
当a≥1时,有2a≥1,∴a≥0,∴a≥1.
4.(2017·全国Ⅰ)设A,B是椭圆C: 长轴的两个端点.若C上存在点
M满足∠AMB=120°,则m的取值范围是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 设焦点在x轴上,点M(x,y).
过点M作x轴的垂线,交x轴于点N,
则N(x,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于焦点在y轴上的情况,同理亦可得m≥9.
则m的取值范围是(0,1]∪[9,+∞).
方法二 当0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得0
要使C上存在点M满足∠AMB=120°,
故m的取值范围为(0,1]∪[9,+∞).
5.(2018·全国Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.已知bsin C
+csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 △ABC的内角A,B,C的对边分别为a,b,c,
bsin C+csin B=4asin Bsin C,
利用正弦定理可得sin Bsin C+sin Csin B=4sin Asin Bsin C,
由于0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于b2+c2-a2=8,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 ∵bsin C+csin B=4asin Bsin C,
∴由正弦定理得sin Bsin C+sin Csin B=4sin Asin Bsin C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(2014·福建)函数f(x)= 的零点个数是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
所以在(-∞,0]上有一个零点.
所以f(x)在(0,+∞)上单调递增.
又因为f(2)=-2+ln 2<0,f(3)=ln 3>0,f(2)·f(3)<0,
所以f(x)在(2,3)内有一个零点.
综上,函数f(x)的零点个数为2.
7.(2017·全国Ⅰ)已知函数f(x)=ex(ex-a)-a2x.
(1)讨论f(x)的单调性;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 函数f(x)的定义域为(-∞,+∞),
f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).
①若a=0,则f(x)=e2x在(-∞,+∞)上单调递增.
②若a>0,则由f′(x)=0,得x=ln a.
当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
故f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若f(x)≥0,求a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ①若a=0,则f(x)=e2x,所以f(x)>0,符合题意.
②若a>0,则由(1)知,当x=ln a时,f(x)取得最小值,
最小值为f(ln a)=-a2ln a,
从而当且仅当-a2ln a≥0,即0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即 ≤a<0时,f(x)≥0.
综上,a的取值范围是[ ,1].
8.(2018·全国Ⅰ)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线BM的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当l与x轴垂直时,l的方程为x=2,可得点M的坐标为(2,2)或(2,-2).
即x-2y+2=0或x+2y+2=0.
(2)证明:∠ABM=∠ABN.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 当l与x轴垂直时,AB为MN的垂直平分线,
所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为y=k(x-2)(k≠0),
M(x1,y1),N(x2,y2),则x1>0,x2>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以kBM+kBN=0,可知BM,BN的倾斜角互补,
所以∠ABM=∠ABN.
综上,∠ABM=∠ABN.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 由m是1和9的等比中项,可得m=±3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
该曲线为焦点在y轴上的椭圆,
该曲线为焦点在x轴上的双曲线,
10.(2021·遂宁模拟)已知过点(0,2)的直线l与圆心为C的圆(x-2)2+(y-1)2=10相交于A,B两点,若CA⊥CB,则直线l的方程为
A.2x-y+2=0
B.2x-y+2=0或2x+y-2=0
C.x=0
D.x=0或2x+y-2=0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以△ABC是以∠ACB为直角的等腰直角三角形,
若直线l的斜率不存在,则直线l的方程为x=0,
此时点C到直线l的距离为2,不符合题意;
若直线l的斜率存在,设直线l的方程为y=kx+2,即kx-y+2=0,
整理得(k-2)2=0,解得k=2,
所以直线l的方程为y=2x+2,即2x-y+2=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.若不等式(a-2)x2+2(a-2)x-4<0对任意实数x均成立,则实数a的取值范围是
A.(-2,2) B.[-2,2]
C.(2,+∞) D.(-2,2]
√
解析 当a-2=0,即a=2时,此时-4<0恒成立,满足条件;
当a-2≠0时,因为(a-2)x2+2(a-2)x-4<0对任意实数x都成立,
解得a∈(-2,2),综上可知,a∈(-2,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由已知得f′(x)=a(sin x+xcos x),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又函数图象是连续不断的,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又函数图象是连续不断的,
13.已知集合A={x|-2≤x≤7},B={x|m+1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(-∞,4]
解析 当B= 时,有m+1≥2m-1,则m≤2;
当B≠ 时,若B A,如图.
综上,m的取值范围为(-∞,4].
14.(2021·杭州模拟)一排有11个座位,现安排2人就座,规定中间的3个座位不能坐,且2人不相邻,则不同排法的种数是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
44
解析 根据两人在三个空位同侧与异侧进行分类,
即共6+6+32=44(种).
15.(2021·柳州模拟)已知数列{an}的前n项和是Sn,且满足Sn=2an-1,n∈N*.
(1)求数列{an}的通项公式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 依题意得,当n=1时,有S1=2a1-1,
又S1=a1,故a1=1,
又Sn=2an-1, ①
当n≥2时,有Sn-1=2an-1-1, ②
①-②得Sn-Sn-1=an=2an-2an-1,
化简得an=2an-1,
∴{an}是以1为首项,2为公比的等比数列,
∴an=2n-1.
(2)若bn=2n-1,且数列{cn}由a1,b1,a2,b2,a3,b3,…,an,bn,…组成,求{cn}的前n项和Tn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当n为偶数时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tn=a1+b1+a2+b2+a3+b3+…+
=a1+a2+a3+…+ +b1+b2+b3+…+
=
=
=
当n为奇数时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tn=a1+b1+a2+b2+a3+b3+…+
=a1+a2+a3+…+ +b1+b2+b3+…+
=
=
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=
∴Tn=
16.(2021·丰台区模拟)已知椭圆C: ,过点(-1,0)的直线l交椭圆C于点A,B.
(1)当直线l与x轴垂直时,求|AB|;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当直线l与x轴垂直时,其方程为x=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①当直线l斜率存在时,
设直线l的方程为y=k(x+1),A(x1,y1),B(x2,y2),
得(1+3k2)x2+6k2x+3k2-3=0.显然Δ>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=x1x2-m(x1+x2)+m2+k2(x1+1)(x2+1)
=x1x2-m(x1+x2)+m2+k2x1x2+k2(x1+x2)+k2
=(k2-m)(x1+x2)+(k2+1)x1x2+k2+m2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②当直线l与x轴垂直时,
考情分析
练后疑难精讲
分类讨论思想是当问题的对象不能进行统一研究时,就需要对研究的对象按某个标准进行分类,然后对每一类分别研究,给出每一类的结论,最终综合各类结果得到整个问题的解答.实质上分类讨论就是“化整为零,各个击破,再集零为整”的数学思想.
一、由概念、法则、公式、性质引起的分类讨论
核心提炼
解决由概念、法则、公式引起的分类讨论问题的步骤
第一步:确定需分类的目标与对象.即确定需要分类的目标,一般把需要用到公式、定理解决问题的对象作为分类目标.
第二步:根据公式、定理确定分类标准.运用公式、定理对分类对象进行区分.
第三步:分类解决“分目标”问题.对分类出来的“分目标”分别进行处理.
第四步:汇总“分目标”.将“分目标”问题进行汇总,并作进一步处理.
题号 1 5 6 10 13 14 15
二、由参数变化引起的分类讨论
核心提炼
含有参数的分类讨论问题主要包括:(1)含有参数的不等式的求解;(2)含有参数的方程的求解;(3)函数解析式中含参数的最值与单调性问题;(4)二元二次方程表示曲线类型的判定等.求解这类问题的一般思路是:结合参数的意义及参数对结果的影响进行分类讨论.讨论时,应全面分析参数变化引起结论的变化情况,参数有几何意义时还要考虑适当地运用数形结合思想.
题号 3 4 7 11 12
三、由图形位置或形状引起的分类讨论
核心提炼
1.一般由图形的位置或形状变动引发的讨论包括:二次函数对称轴位置的变动;函数问题中区间的变动;函数图象形状的变动;直线由斜率引起的位置变动;圆锥曲线由焦点引起的位置变动或由离心率引起的形状变动;立体几何中点、线、面的位置变动等.
2.圆锥曲线形状不确定时,常按椭圆、双曲线来分类讨论,求圆锥曲线的方程时,常按焦点的位置不同来分类讨论.
3.相关计算中,涉及图形问题时,也常按图形的位置不同、大小差异等来分类讨论.
题号 2 8 9 16
1
2
3
4
5
易错对点精补
1.[T1补偿](2021·房山区模拟)“a2=1”是“直线x+ay=1与ax+y=1平行”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
√
1
2
3
4
5
解析 因为直线x+ay=1与ax+y=1平行,
解得a=±1;
而当a=1时,直线x+ay=1为x+y=1,
同时ax+y=1为x+y=1,两直线重合不满足题意;
当a=-1时,x-y=1与-x+y=1平行,满足题意;
故a=-1,根据小范围推大范围可得,
a2=1是a=-1的必要不充分条件.
1
2
3
4
5
√
1
2
3
4
5
1
2
3
4
5
3.[T6补偿]已知λ∈R,函数f(x)= 当λ=2时,不等式f(x)<0
的解集是_____.若函数f(x)恰有2个零点,则λ的取值范围是_______________.
(1,4)
(1,3]∪(4,+∞)
1
2
3
4
5
所以2≤x<4或1
此时令f(x)=x2-4x+3=0,解得x=1或x=3,
即在(-∞,λ)上有两个零点,满足题意;
当λ≤4时,令f(x)=x-4=0,解得x=4,
由f(x)=x2-4x+3在(-∞,λ)上只能有一个零点得1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
4.[T12补偿]若函数f(x)=mx2-x+ln x存在单调递减区间,则实数m的取
值范围是__________.
1
2
3
4
5
1
2
3
4
5
即2mx2-x+1<0在(0,+∞)上有解.
当m≤0时显然成立;当m>0时,
5.[T7补偿](2021·洛阳模拟)已知函数f(x)=ax-x2-ln x(a∈R).
(1)求函数f(x)的单调区间;
1
2
3
4
5
1
2
3
4
5
由f′(x)>0得x1
1
2
3
4
5
函数f(x)的单调递减区间为(0,+∞),无单调递增区间;
(2)若函数f(x)存在极值,且这些极值的和大于5+ln 2,求实数a的取值范围.
1
2
3
4
5
1
2
3
4
5
此时方程2x2-ax+1=0有两个不相等的正根x1,x2,
=a(x1+x2)-[(x1+x2)2-2x1x2]-ln(x1x2)
1
2
3
4
5
∴a的取值范围是(4,+∞).
同课章节目录
