第32练 转化与化归思想 课件(共58张PPT)
文档属性
| 名称 | 第32练 转化与化归思想 课件(共58张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 17:01:24 | ||
图片预览




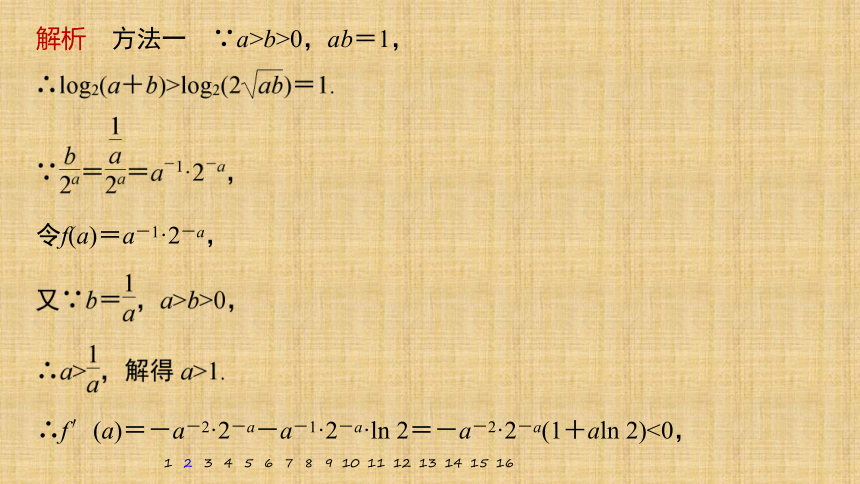







文档简介
(共58张PPT)
转化与化归思想
第32练
专项典题精练
高考汇编
1.(2021·浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R),若f(s-t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)=ax2+b,
所以f(s-t)=a(s-t)2+b,f(s)=as2+b,f(s+t)=a(s+t)2+b.
因为f(s-t),f(s),f(s+t)成等比数列,
所以f2(s)=f(s-t)f(s+t),
即(as2+b)2=[a(s-t)2+b]·[a(s+t)2+b],
化简得-2a2s2t2+a2t4+2abt2=0,
得t=0或2as2-at2=2b,
易知点(s,t)的轨迹为一条直线和一条双曲线.
2.(2017·山东)若a>b>0,且ab=1,则下列不等式成立的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 ∵a>b>0,ab=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f(a)=a-1·2-a,
∴f′(a)=-a-2·2-a-a-1·2-a·ln 2=-a-2·2-a(1+aln 2)<0,
∴f(a)在(1,+∞)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 ∵a>b>0,ab=1,
3.(2015·全国Ⅱ)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为
A.36π B.64π C.144π D.256π
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图,要使三棱锥O-ABC即C-OAB的体积最大,当且仅当点C到平面OAB的距离,
即三棱锥C-OAB底面OAB上的高最大,其最大值为球O的半径R,
所以R=6,得S球O=4πR2=4π×62=144π.
4.(2019·浙江)设a,b∈R,函数f(x)= 若函数y=f(x)-ax-b恰有3个零点,则
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由题意可得,当x≥0时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f(x)-ax-b=0,
因为对任意的x∈R,f(x)-ax-b=0有3个不同的实数根,
所以要使满足条件,则当x≥0时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以b<0.
5.(2019·江苏)从3名男同学和2名女同学中任选2名同学参加志愿者服务,
则选出的2名同学中至少有1名女同学的概率是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 从3名男同学和2名女同学中任选2名同学参加志愿者服务,
6.(2019·北京)设函数f(x)=ex+ae-x(a为常数).若f(x)为奇函数,则a=____;若f(x)是R上的增函数,则a的取值范围是__________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-1
(-∞,0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x),e-x+aex=-ex-ae-x,
∴(1+a)e-x+(1+a)ex=0,
∴a=-1;
∵f(x)在R上单调递增,
∴e2x-a≥0,a≤0,故a的取值范围是(-∞,0].
(1)求f(x)的定义域与最小正周期;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)讨论f(x)在区间 上的单调性.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2019·全国Ⅰ)已知函数f(x)=2sin x-xcos x-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)上存在唯一零点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故g(x)在(0,π)上存在唯一零点.
所以f′(x)在区间(0,π)上存在唯一零点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 设g(x)=f′(x),
则g(x)=cos x+xsin x-1,g′(x)=xcos x.
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题设知f(π)≥aπ,f(π)=0,可得a≤0.
由(1)知,f′(x)在(0,π)上只有一个零点,
设为x0,且当x∈(0,x0)时,f′(x)>0;
当x∈(x0,π)时,f′(x)<0,
所以f(x)在(0,x0)上单调递增,在(x0,π)上单调递减.
又f(0)=0,f(π)=0,
所以当x∈[0,π]时,f(x)≥0.
又当a≤0,x∈[0,π]时,ax≤0,故f(x)≥ax.
因此,a的取值范围是(-∞,0].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
9.(2021·烟台模拟)已知f(x)是定义在R上的奇函数,f(2-x)=f(x),当x∈
[0,1]时,f(x)=x3,则
A.f(2 021)=0
B.2是f(x)的一个周期
C.当x∈(1,3)时,f(x)=(1-x)3
D.f(x)>0的解集为(4k,4k+2)(k∈Z)
√
解析 因为f(x)是定义在R上的奇函数,
所以f(2-x)=f(x)=-f(-x),
所以f(2+x)=-f(x),
所以f(4+x)=-f(2+x)=f(x),
所以f(x)的最小正周期是4,故B错误.
f(2 021)=f(1)=1,故A错误.
因为当x∈[0,1]时,f(x)=x3,f(x)是定义在R上的奇函数,
所以当x∈[-1,1]时,f(x)=x3,
当x∈(1,3)时,2-x∈(-1,1),f(x)=f(2-x)=(2-x)3,故C错误.
因为当x∈(0,2)时,f(x)>0,f(x)的最小正周期是4,
所以f(x)>0的解集为(4k,4k+2)(k∈Z),故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.(2021·晋中模拟)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为
A.12π B.20π C.24π D.32π
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 将三棱锥P-ABC放入长方体中,如图,
三棱锥P-ABC的外接球就是长方体的外接球.
因为PA=AB=2,AC=4,△ABC为直角三角形,
设外接球的半径为R,
依题意可得(2R)2=4+4+12=20,
故R2=5,
则球O的表面积为S=4πR2=20π.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·郑州模拟)在矩形ABCD中,AB=4,AD=3,M,N分别是AB,AD上的动点,且满足2AM+AN=1,设 ,则2x+3y的最小值为
A.48 B.49 C.50 D.51
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,建立平面直角坐标系,
则A(0,0),B(4,0),C(4,3),D(0,3),
设M(m,0),N(0,n),因为2AM+AN=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(多选)(2021·汕头模拟)已知定义在R上的奇函数,满足f(2-x)+f(x)=0,当x∈(0,1]时,f(x)=-log2x,若函数F(x)=f(x)-tan πx,在区间[-1,m]上有10个零点,则m的取值可以是
A.3.8 B.3.9 C.4 D.4.1
√
√
解析 f(x)是奇函数,则f(-x)=-f(x),
又f(2-x)+f(x)=0,f(2-x)=-f(x)=f(-x),
令t=-x得f(t)=f(t+2),即f(x)=f(x+2),
所以f(x)是周期函数,周期为2,
又f(x)是R上的奇函数,
所以f(0)=f(2)=f(4)=…=0,f(1)=0,
所以f(n)=0,n∈Z,
作出y=f(x)和y=tan πx的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图,由图可知x≥-1时,从点A(-1,0),10个交点依次为A,B,O,C,D,E,F,G,H,I,点J是第11个交点,J(4,0),
设C点横坐标为x0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即3.5所以m可取3.8,3.9,m≥4时至少有11个零点.
13.(2021·沈阳模拟)若“ x∈ ,使得2x2-λx-1<0成立”是假命题,
则实数λ的取值范围为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
λ≤-1
14.已知球O是三棱锥P-ABC的外接球,PA=AB=PB=AC=2,CP=
,点D是PB的中点,且CD= ,则球O的表面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得CP2=PA2+AC2,所以PA⊥AC,
由点D是PB的中点,且PA=AB=PB=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得CD2=AD2+AC2,所以AD⊥AC,
又AD∩AP=A且AD,AP 平面PAB,
所以AC⊥平面PAB,
以△PAB为底面,AC为侧棱补成一个直三棱柱,如图所示,
则三棱锥P-ABC的外接球即为该三棱柱的外接球,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为0.1,0.2,0.3,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设“部件1需要调整”为事件A,“部件2需要调整”为事件B,“部件3需要调整”为事件C,
由题意可知,P(A)=0.1,P(B)=0.2,P(C)=0.3.
部件1,2中至少有1个需要调整的概率为
1-[1-P(A)][1-P(B)]=1-0.9×0.8=1-0.72=0.28.
(2)记设备在一天的运转中需要调整的部件个数为X,求X的分布列及均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意可知X的可能取值为0,1,2,3.
且P(X=0)=[1-P(A)][1-P(B)][1-P(C)]=(1-0.1)×(1-0.2)×(1-0.3)=0.504,
P(X=1)=P(A)[1-P(B)][1-P(C)]+[1-P(A)]·P(B)[1-P(C)]+[1-P(A)][1-P(B)]P(C)
=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398,
P(X=2)=P(A)P(B)[1-P(C)]+P(A)[1-P(B)]·P(C)+[1-P(A)]P(C)P(B)
=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092.
P(X=3)=P(A)P(B)P(C)=0.1×0.2×0.3=0.006,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 1 2 3
P 0.504 0.398 0.092 0.006
其均值E(X)=0.504×0+0.398×1+0.092×2+0.006×3=0.6.
16.(2021·渭南模拟)已知函数f(x)=aln x+x(a≠0),g(x)=ex+bx2(b∈R).
(1)记h(x)=f(x)+x2,试讨论函数h(x)的单调性;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
记φ(x)=2x2+x+a(x>0),
当a>0时,h′(x)>0,h(x)在(0,+∞)上单调递增,
当a<0时,Δ=1-8a>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若曲线y=f(x)与曲线y=g(x)在x=1处的切线都过点(0,1).求证:当x>0
时,f(x)+ ≥e-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f′(1)=a+1,f(x)在x=1处的切线方程为y-1=(a+1)(x-1),过点(0,1)得a=-1,
g′(1)=e+2b,g(x)在x=1处的切线方程为y-e-b=(e+2b)(x-1),过点(0,1)得b=-1,
∴f(x)=-ln x+x,g(x)=ex-x2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵当x>0时,ex-1>0,
∴当x∈(0,1)时,K′(x)<0,K(x)在(0,1)上单调递减,
∴当x∈(1,+∞)时,K′(x)>0,K(x)在(1,+∞)上单调递增,
∴K(x)≥K(1)=0,故原不等式成立.
考情分析
练后疑难精讲
转化和化归思想一般是将复杂的问题通过变换转化为简单的问题,将难解的问题通过变换转化为容易求解的问题,将未解决的问题通过变换转化为已解决的问题.转化和化归思想在高考中起到十分重要的作用,数学问题的解决,总离不开转化和化归,它几乎可以渗透到所有的数学内容和解题过程中.
一、特殊与一般的转化
核心提炼
化一般为特殊的应用要点
把一般问题特殊化,解答选择题、填空题常能起到事半功倍的效果,既准确又迅速.常用的特例有特殊值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等,要注意恰当利用所学知识、恰当选择特殊量.
题号 2 3 10 14
二、正与反、常量与变量的转化
核心提炼
正与反的转化,体现“正难则反”的原则,先从正面求解,再取正面答案的补集即可.一般地,题目若出现多种成立的情形,则不成立的情形相对很少,从反面考虑较简单.因此,间接法多用于含有“至多”“至少”及否定性命题情形的问题中.
题号 5 13 15
三、函数、方程、不等式之间的转化
核心提炼
函数、方程与不等式就像“一胞三兄弟”,解决方程、不等式的问题需要函数帮助,解决函数的问题需要方程、不等式的帮助,因此借助于函数、方程、不等式进行转化与化归可以将问题化繁为简,一般可将不等式关系转化为最值(值域)问题,从而求出参变量的范围.
题号 1 4 6 7 8 9 11 12 16
1
2
3
4
5
易错对点精补
1.[T2补偿]在△ABC中,三边长a,b,c满足a+c=3b,则 的
值为
√
解析 令a=4,c=5,b=3,则符合题意.
1
2
3
4
5
2.[T10补偿](2021·南昌模拟)已知在三棱锥A-BCD中,侧面ABC⊥底面BCD,△ABC是边长为3的正三角形,△BCD是直角三角形,且∠BCD=90°,CD=2,则此三棱锥外接球的体积等于
√
1
2
3
4
5
解析 在三棱锥A-BCD中,侧面ABC⊥底面BCD,把该三棱锥放入长方体中,如图所示.
设三棱锥外接球的球心为O,取BC的中点M,BD的中点N,△ABC的重心G,连接OG,
1
2
3
4
5
3.[T5补偿](2021·天津模拟)甲、乙两名同学进行篮球投篮练习,甲同学一
次投篮命中的概率为 ,乙同学一次投篮命中的概率为 ,假设两人投篮
命中与否互不影响,则甲、乙两人各投篮一次,至少有一人命中的概率
是___.
4.[T13补偿]已知命题p: x∈[0,2],x2+ax-1≤0是假命题,则实数a的
取值范围为____________.
1
2
3
4
5
1
2
3
4
5
解析 由条件可知命题p的否定: x∈[0,2],x2+ax-1>0是真命题,
当x=0时,-1>0不成立;
(1)求函数f(x)的最小正周期和单调递减区间;
1
2
3
4
5
1
2
3
4
5
(2)若对任意的m∈(-2,2),方程f(x)=m(其中x∈[0,a))始终有两个不同的根x1,x2.
①求实数a的值;
1
2
3
4
5
②求x1+x2的值.
1
2
3
4
5
解 根据三角函数图象的对称性,
转化与化归思想
第32练
专项典题精练
高考汇编
1.(2021·浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R),若f(s-t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)=ax2+b,
所以f(s-t)=a(s-t)2+b,f(s)=as2+b,f(s+t)=a(s+t)2+b.
因为f(s-t),f(s),f(s+t)成等比数列,
所以f2(s)=f(s-t)f(s+t),
即(as2+b)2=[a(s-t)2+b]·[a(s+t)2+b],
化简得-2a2s2t2+a2t4+2abt2=0,
得t=0或2as2-at2=2b,
易知点(s,t)的轨迹为一条直线和一条双曲线.
2.(2017·山东)若a>b>0,且ab=1,则下列不等式成立的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 方法一 ∵a>b>0,ab=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f(a)=a-1·2-a,
∴f′(a)=-a-2·2-a-a-1·2-a·ln 2=-a-2·2-a(1+aln 2)<0,
∴f(a)在(1,+∞)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 ∵a>b>0,ab=1,
3.(2015·全国Ⅱ)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为
A.36π B.64π C.144π D.256π
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图,要使三棱锥O-ABC即C-OAB的体积最大,当且仅当点C到平面OAB的距离,
即三棱锥C-OAB底面OAB上的高最大,其最大值为球O的半径R,
所以R=6,得S球O=4πR2=4π×62=144π.
4.(2019·浙江)设a,b∈R,函数f(x)= 若函数y=f(x)-ax-b恰有3个零点,则
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由题意可得,当x≥0时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f(x)-ax-b=0,
因为对任意的x∈R,f(x)-ax-b=0有3个不同的实数根,
所以要使满足条件,则当x≥0时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以b<0.
5.(2019·江苏)从3名男同学和2名女同学中任选2名同学参加志愿者服务,
则选出的2名同学中至少有1名女同学的概率是____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 从3名男同学和2名女同学中任选2名同学参加志愿者服务,
6.(2019·北京)设函数f(x)=ex+ae-x(a为常数).若f(x)为奇函数,则a=____;若f(x)是R上的增函数,则a的取值范围是__________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-1
(-∞,0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f(x)为奇函数,
∴f(-x)=-f(x),e-x+aex=-ex-ae-x,
∴(1+a)e-x+(1+a)ex=0,
∴a=-1;
∵f(x)在R上单调递增,
∴e2x-a≥0,a≤0,故a的取值范围是(-∞,0].
(1)求f(x)的定义域与最小正周期;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)讨论f(x)在区间 上的单调性.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.(2019·全国Ⅰ)已知函数f(x)=2sin x-xcos x-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)上存在唯一零点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故g(x)在(0,π)上存在唯一零点.
所以f′(x)在区间(0,π)上存在唯一零点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 设g(x)=f′(x),
则g(x)=cos x+xsin x-1,g′(x)=xcos x.
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题设知f(π)≥aπ,f(π)=0,可得a≤0.
由(1)知,f′(x)在(0,π)上只有一个零点,
设为x0,且当x∈(0,x0)时,f′(x)>0;
当x∈(x0,π)时,f′(x)<0,
所以f(x)在(0,x0)上单调递增,在(x0,π)上单调递减.
又f(0)=0,f(π)=0,
所以当x∈[0,π]时,f(x)≥0.
又当a≤0,x∈[0,π]时,ax≤0,故f(x)≥ax.
因此,a的取值范围是(-∞,0].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
9.(2021·烟台模拟)已知f(x)是定义在R上的奇函数,f(2-x)=f(x),当x∈
[0,1]时,f(x)=x3,则
A.f(2 021)=0
B.2是f(x)的一个周期
C.当x∈(1,3)时,f(x)=(1-x)3
D.f(x)>0的解集为(4k,4k+2)(k∈Z)
√
解析 因为f(x)是定义在R上的奇函数,
所以f(2-x)=f(x)=-f(-x),
所以f(2+x)=-f(x),
所以f(4+x)=-f(2+x)=f(x),
所以f(x)的最小正周期是4,故B错误.
f(2 021)=f(1)=1,故A错误.
因为当x∈[0,1]时,f(x)=x3,f(x)是定义在R上的奇函数,
所以当x∈[-1,1]时,f(x)=x3,
当x∈(1,3)时,2-x∈(-1,1),f(x)=f(2-x)=(2-x)3,故C错误.
因为当x∈(0,2)时,f(x)>0,f(x)的最小正周期是4,
所以f(x)>0的解集为(4k,4k+2)(k∈Z),故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.(2021·晋中模拟)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为
A.12π B.20π C.24π D.32π
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 将三棱锥P-ABC放入长方体中,如图,
三棱锥P-ABC的外接球就是长方体的外接球.
因为PA=AB=2,AC=4,△ABC为直角三角形,
设外接球的半径为R,
依题意可得(2R)2=4+4+12=20,
故R2=5,
则球O的表面积为S=4πR2=20π.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.(2021·郑州模拟)在矩形ABCD中,AB=4,AD=3,M,N分别是AB,AD上的动点,且满足2AM+AN=1,设 ,则2x+3y的最小值为
A.48 B.49 C.50 D.51
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,建立平面直角坐标系,
则A(0,0),B(4,0),C(4,3),D(0,3),
设M(m,0),N(0,n),因为2AM+AN=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.(多选)(2021·汕头模拟)已知定义在R上的奇函数,满足f(2-x)+f(x)=0,当x∈(0,1]时,f(x)=-log2x,若函数F(x)=f(x)-tan πx,在区间[-1,m]上有10个零点,则m的取值可以是
A.3.8 B.3.9 C.4 D.4.1
√
√
解析 f(x)是奇函数,则f(-x)=-f(x),
又f(2-x)+f(x)=0,f(2-x)=-f(x)=f(-x),
令t=-x得f(t)=f(t+2),即f(x)=f(x+2),
所以f(x)是周期函数,周期为2,
又f(x)是R上的奇函数,
所以f(0)=f(2)=f(4)=…=0,f(1)=0,
所以f(n)=0,n∈Z,
作出y=f(x)和y=tan πx的图象,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图,由图可知x≥-1时,从点A(-1,0),10个交点依次为A,B,O,C,D,E,F,G,H,I,点J是第11个交点,J(4,0),
设C点横坐标为x0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即3.5
13.(2021·沈阳模拟)若“ x∈ ,使得2x2-λx-1<0成立”是假命题,
则实数λ的取值范围为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
λ≤-1
14.已知球O是三棱锥P-ABC的外接球,PA=AB=PB=AC=2,CP=
,点D是PB的中点,且CD= ,则球O的表面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得CP2=PA2+AC2,所以PA⊥AC,
由点D是PB的中点,且PA=AB=PB=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可得CD2=AD2+AC2,所以AD⊥AC,
又AD∩AP=A且AD,AP 平面PAB,
所以AC⊥平面PAB,
以△PAB为底面,AC为侧棱补成一个直三棱柱,如图所示,
则三棱锥P-ABC的外接球即为该三棱柱的外接球,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为0.1,0.2,0.3,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设“部件1需要调整”为事件A,“部件2需要调整”为事件B,“部件3需要调整”为事件C,
由题意可知,P(A)=0.1,P(B)=0.2,P(C)=0.3.
部件1,2中至少有1个需要调整的概率为
1-[1-P(A)][1-P(B)]=1-0.9×0.8=1-0.72=0.28.
(2)记设备在一天的运转中需要调整的部件个数为X,求X的分布列及均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意可知X的可能取值为0,1,2,3.
且P(X=0)=[1-P(A)][1-P(B)][1-P(C)]=(1-0.1)×(1-0.2)×(1-0.3)=0.504,
P(X=1)=P(A)[1-P(B)][1-P(C)]+[1-P(A)]·P(B)[1-P(C)]+[1-P(A)][1-P(B)]P(C)
=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398,
P(X=2)=P(A)P(B)[1-P(C)]+P(A)[1-P(B)]·P(C)+[1-P(A)]P(C)P(B)
=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092.
P(X=3)=P(A)P(B)P(C)=0.1×0.2×0.3=0.006,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故X的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X 0 1 2 3
P 0.504 0.398 0.092 0.006
其均值E(X)=0.504×0+0.398×1+0.092×2+0.006×3=0.6.
16.(2021·渭南模拟)已知函数f(x)=aln x+x(a≠0),g(x)=ex+bx2(b∈R).
(1)记h(x)=f(x)+x2,试讨论函数h(x)的单调性;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
记φ(x)=2x2+x+a(x>0),
当a>0时,h′(x)>0,h(x)在(0,+∞)上单调递增,
当a<0时,Δ=1-8a>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若曲线y=f(x)与曲线y=g(x)在x=1处的切线都过点(0,1).求证:当x>0
时,f(x)+ ≥e-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f′(1)=a+1,f(x)在x=1处的切线方程为y-1=(a+1)(x-1),过点(0,1)得a=-1,
g′(1)=e+2b,g(x)在x=1处的切线方程为y-e-b=(e+2b)(x-1),过点(0,1)得b=-1,
∴f(x)=-ln x+x,g(x)=ex-x2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵当x>0时,ex-1>0,
∴当x∈(0,1)时,K′(x)<0,K(x)在(0,1)上单调递减,
∴当x∈(1,+∞)时,K′(x)>0,K(x)在(1,+∞)上单调递增,
∴K(x)≥K(1)=0,故原不等式成立.
考情分析
练后疑难精讲
转化和化归思想一般是将复杂的问题通过变换转化为简单的问题,将难解的问题通过变换转化为容易求解的问题,将未解决的问题通过变换转化为已解决的问题.转化和化归思想在高考中起到十分重要的作用,数学问题的解决,总离不开转化和化归,它几乎可以渗透到所有的数学内容和解题过程中.
一、特殊与一般的转化
核心提炼
化一般为特殊的应用要点
把一般问题特殊化,解答选择题、填空题常能起到事半功倍的效果,既准确又迅速.常用的特例有特殊值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等,要注意恰当利用所学知识、恰当选择特殊量.
题号 2 3 10 14
二、正与反、常量与变量的转化
核心提炼
正与反的转化,体现“正难则反”的原则,先从正面求解,再取正面答案的补集即可.一般地,题目若出现多种成立的情形,则不成立的情形相对很少,从反面考虑较简单.因此,间接法多用于含有“至多”“至少”及否定性命题情形的问题中.
题号 5 13 15
三、函数、方程、不等式之间的转化
核心提炼
函数、方程与不等式就像“一胞三兄弟”,解决方程、不等式的问题需要函数帮助,解决函数的问题需要方程、不等式的帮助,因此借助于函数、方程、不等式进行转化与化归可以将问题化繁为简,一般可将不等式关系转化为最值(值域)问题,从而求出参变量的范围.
题号 1 4 6 7 8 9 11 12 16
1
2
3
4
5
易错对点精补
1.[T2补偿]在△ABC中,三边长a,b,c满足a+c=3b,则 的
值为
√
解析 令a=4,c=5,b=3,则符合题意.
1
2
3
4
5
2.[T10补偿](2021·南昌模拟)已知在三棱锥A-BCD中,侧面ABC⊥底面BCD,△ABC是边长为3的正三角形,△BCD是直角三角形,且∠BCD=90°,CD=2,则此三棱锥外接球的体积等于
√
1
2
3
4
5
解析 在三棱锥A-BCD中,侧面ABC⊥底面BCD,把该三棱锥放入长方体中,如图所示.
设三棱锥外接球的球心为O,取BC的中点M,BD的中点N,△ABC的重心G,连接OG,
1
2
3
4
5
3.[T5补偿](2021·天津模拟)甲、乙两名同学进行篮球投篮练习,甲同学一
次投篮命中的概率为 ,乙同学一次投篮命中的概率为 ,假设两人投篮
命中与否互不影响,则甲、乙两人各投篮一次,至少有一人命中的概率
是___.
4.[T13补偿]已知命题p: x∈[0,2],x2+ax-1≤0是假命题,则实数a的
取值范围为____________.
1
2
3
4
5
1
2
3
4
5
解析 由条件可知命题p的否定: x∈[0,2],x2+ax-1>0是真命题,
当x=0时,-1>0不成立;
(1)求函数f(x)的最小正周期和单调递减区间;
1
2
3
4
5
1
2
3
4
5
(2)若对任意的m∈(-2,2),方程f(x)=m(其中x∈[0,a))始终有两个不同的根x1,x2.
①求实数a的值;
1
2
3
4
5
②求x1+x2的值.
1
2
3
4
5
解 根据三角函数图象的对称性,
同课章节目录
