第33练 客观题的解法 课件(共42张PPT)
文档属性
| 名称 | 第33练 客观题的解法 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 17:02:12 | ||
图片预览


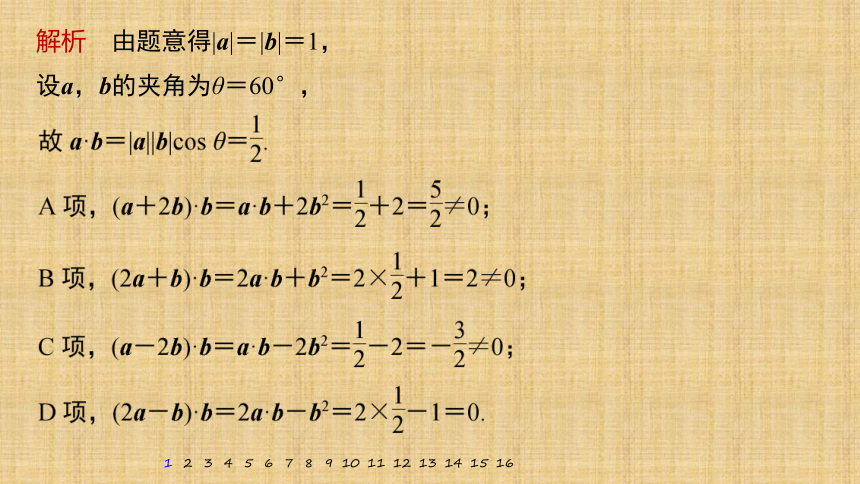









文档简介
(共42张PPT)
客观题的解法
第33练
专项典题精练
高考汇编
1.(2020·全国Ⅱ)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是
A.a+2b B.2a+b C.a-2b D.2a-b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由题意得|a|=|b|=1,
设a,b的夹角为θ=60°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(2014·全国Ⅱ)函数f(x)在x=x0处导数存在.若p:f′(x0)=0;q:x=x0是f(x)的极值点,则
A.p是q的充要条件
B.p是q的充分不必要条件
C.p是q的必要不充分条件
D.p既不是q的充分条件,也不是q的必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当f′(x0)=0时,x=x0不一定是f(x)的极值点,
比如,y=x3在x=0时,f′(0)=0,
但在x=0的左右两侧f′(x)的符号相同,
因而x=0不是y=x3的极值点.
由极值的定义知,x=x0是f(x)的极值点必有f′(x0)=0.
综上知,p是q的必要不充分条件.
3.(2020·浙江)函数y=xcos x+sin x在区间[-π,π]上的图象可能为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 令f(x)=y=xcos x+sin x,
则f(-x)=-xcos x-sin x=-f(x),
所以f(x)为奇函数,排除C,D.
当x=π时,f(π)=-π<0,排除B.
√
4.(2015·安徽)下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由双曲线性质知A,B项双曲线焦点在x轴上,不合题意;
C,D项双曲线焦点均在y轴上,
5.(2021·全国乙卷)设函数f(x)= ,则下列函数中为奇函数的是
A.f(x-1)-1 B.f(x-1)+1
C.f(x+1)-1 D.f(x+1)+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
定义域关于原点对称,但不满足F(x)=-F(-x);
定义域关于原点对称,且满足G(x)=-G(-x);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
定义域不关于原点对称;
定义域不关于原点对称.
为保证函数变换之后为奇函数,
需将函数y=f(x)的图象向右平移一个单位长度,再向上平移一个单位长度,
得到的图象对应的函数为y=f(x-1)+1.
6.(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当a1<0,q>1时,an=a1qn-1<0,
此时数列{Sn}单调递减,
所以甲不是乙的充分条件.
当数列{Sn}单调递增时,有Sn+1-Sn=an+1=a1qn>0,
若a1>0,则qn>0(n∈N*),即q>0;
若a1<0,则qn<0(n∈N*),不存在.
所以甲是乙的必要条件.
7.(2021·浙江)已知多项式(x-1)3+(x+1)4=x4+a1x3+a2x2+a3x+a4,则a1=____,a2+a3+a4=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5
10
令x=1时,则有1+a1+a2+a3+a4=24=16,
所以a2+a3+a4=16-5-1=10.
8.(2017·北京)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:
(1)男学生人数多于女学生人数;
(2)女学生人数多于教师人数;
(3)教师人数的两倍多于男学生人数.
①若教师人数为4,则女学生人数的最大值为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6
解析 若教师人数为4,
则男学生人数小于8,最大值为7,女学生人数最大时应比男学生人数少1人,
所以女学生人数的最大值为7-1=6.
②该小组人数的最小值为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12
解析 设男学生人数为x(x∈N*),要求该小组人数的最小值,
则女学生人数为x-1,教师人数为x-2.
又2(x-2)>x,解得x>4,即x=5,
该小组人数的最小值为5+4+3=12.
9.(2021·北京房山区模拟)已知a,b∈R,且a>b,则下列各式中一定成立的是
A. B.a3>b3
C.ab>b2 D.2|a|>2|b|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 因为a,b∈R,且a>b,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,因为函数y=x3在定义域R上单调递增,
所以a3>b3,故B正确;
对于C,若b=0,
则ab=b2=0,故C错误;
对于D,若a=1,b=-1,
则2|a|=2|b|,故D错误.
A.20 B.15
C.9 D.6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设四边形ABCD为矩形,建系如图,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
函数f(x)为奇函数,排除BC选项;
所以f(x)<0,排除D选项.
故过P,Q,C三点的截面把棱柱分成的两部分体积之比为2∶1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.如图,在棱柱的侧棱A1A和B1B上各有一动点P,Q满足A1P=BQ,过P,Q,C三点的截面把棱柱分成两部分,则其体积之比为
A.3∶1 B.2∶1
C.4∶1 D.
√
解析 令P与A1重合,Q与B重合,
此时A1P=BQ=0,
则 ,
13.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.2 B.3
C.-3 D.-4
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
且x→+∞时,t→0,
∴只需关于t的方程(m+2)t2-2mt+1=0(*)有且只有一个正实根.
15.若(2x+4)2n=a0+a1x+a2x2+…+a2nx2n(n∈N*),则a2+a4+…+a2n被3除的余数是__.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 令x=0,得a0=42n.
分别令x=1和x=-1,将得到的两式相加,
被3除的余数是1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.现有灰色与白色的卡片各八张,分别写有数字1到8.甲、乙、丙、丁四个人每人面前摆放四张,并按从小到大的顺序自左向右排列(当灰色卡片和白色卡片数字相同时,白色卡片摆在灰色卡片的右侧).如图,甲面前的四张卡片已经翻开,则写有数字4的灰色卡片是___.(填写字母)
K
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得E=1,J=2,L=8,
假设H=4,则F=3,G=4,
此时白色的“4”在灰色的“4”的左边,
不符合题意,所以假设不成立.
假设K=4,则由题意得
白2,灰3,白7,灰8;灰1,白5,白6,灰7;
白1,灰2,灰4,白8;白3,白4,灰5,灰6.
故K=4时,符合题意.
考情分析
练后疑难精讲
高考数学选择题主要考查对基础知识的理解、基本技能的熟练程度、基本计算的准确性、基本方法的正确运用、考虑问题的严谨、解题速度的快捷等方面,注重多个知识点的小型综合,渗透各种数学思想和方法,能充分考查灵活应用基础知识解决数学问题的能力.
一、特(例)值法
核心提炼
从题干(或选项)出发,通过选取符合条件的特殊情况(特殊值、特殊点、特殊位置、特殊函数等)代入,将问题特殊化或构造满足题设条件的特殊函数或图形位置进行判断.特殊化法是“小题小做”的重要策略.
题号 2 6 7 8 9 10 12 15
二、排除法
核心提炼
排除法(淘汰法)是充分利用单项选择题有且只有一个正确的选项这一特征,通过分析、推理、计算、判断,排除不符合要求的选项,从而得出正确结论的一种方法.
题号 3 4 11 13
三、验证法
核心提炼
验证法从题设条件出发,运用有关概念、性质、定理、法则和公式等知识,逐一检验选项得出答案.
题号 1 5 14 16
1
2
3
4
5
易错对点精补
6
1.[T1补偿](2021·平顶山模拟)已知数列{an}的前n项和为Sn,Sn=n2an,a1=1,则Sn等于
√
2.[T9补偿](2021·信阳模拟)对于任意非零实数a,b,且a>b,又c∈R,则有
A.lg(a-b)>0 B.ac2C.a2>b2 D.
1
2
3
4
5
√
6
解析 当a=2,b=1时,lg(a-b)=0,故A错误;
当c=0时,ac2=bc2,故B错误;
当a=1,b=-1时,a2=b2,故C错误;
1
2
3
4
5
3.[T3补偿](2021·常州模拟)函数f(x)=sin x· 的图象大致是
6
√
1
2
3
4
5
6
可得f(0)=0,可排除B,C选项;
所以函数f(x)为偶函数,所以排除D选项.
1
2
3
4
5
6
A.36 B.24 C.18 D.12
√
解析 取特殊函数,根据条件可设f(x)=3x,
1
2
3
4
5
6
√
1
2
3
4
5
解析 因为函数f(x)的最小值为-2+1=-1,
由函数f(x)的图象与直线y=-1相邻两个交点的距离为π可得,
该函数的最小正周期为T=π,
6
故f(x)=2sin(2x+φ)+1.
由f(x)>1,可得sin(2x+φ)>0.
1
2
3
4
5
6
6.[T12补偿]如图,在三棱锥O—ABC中,三条棱OA,OB,OC两两垂直,且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3的大小关系为________.
1
2
3
4
5
6
S3解析 要满足各个截面使分得的两个三棱锥体积相等,
则需满足与截面对应的交点E,F,G分别为中点即可.
故可以将三条棱长分别取为OA=6,OB=4,OC=2,如图,
1
2
3
4
5
6
故S3
客观题的解法
第33练
专项典题精练
高考汇编
1.(2020·全国Ⅱ)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是
A.a+2b B.2a+b C.a-2b D.2a-b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由题意得|a|=|b|=1,
设a,b的夹角为θ=60°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(2014·全国Ⅱ)函数f(x)在x=x0处导数存在.若p:f′(x0)=0;q:x=x0是f(x)的极值点,则
A.p是q的充要条件
B.p是q的充分不必要条件
C.p是q的必要不充分条件
D.p既不是q的充分条件,也不是q的必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当f′(x0)=0时,x=x0不一定是f(x)的极值点,
比如,y=x3在x=0时,f′(0)=0,
但在x=0的左右两侧f′(x)的符号相同,
因而x=0不是y=x3的极值点.
由极值的定义知,x=x0是f(x)的极值点必有f′(x0)=0.
综上知,p是q的必要不充分条件.
3.(2020·浙江)函数y=xcos x+sin x在区间[-π,π]上的图象可能为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 令f(x)=y=xcos x+sin x,
则f(-x)=-xcos x-sin x=-f(x),
所以f(x)为奇函数,排除C,D.
当x=π时,f(π)=-π<0,排除B.
√
4.(2015·安徽)下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由双曲线性质知A,B项双曲线焦点在x轴上,不合题意;
C,D项双曲线焦点均在y轴上,
5.(2021·全国乙卷)设函数f(x)= ,则下列函数中为奇函数的是
A.f(x-1)-1 B.f(x-1)+1
C.f(x+1)-1 D.f(x+1)+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
定义域关于原点对称,但不满足F(x)=-F(-x);
定义域关于原点对称,且满足G(x)=-G(-x);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
定义域不关于原点对称;
定义域不关于原点对称.
为保证函数变换之后为奇函数,
需将函数y=f(x)的图象向右平移一个单位长度,再向上平移一个单位长度,
得到的图象对应的函数为y=f(x-1)+1.
6.(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当a1<0,q>1时,an=a1qn-1<0,
此时数列{Sn}单调递减,
所以甲不是乙的充分条件.
当数列{Sn}单调递增时,有Sn+1-Sn=an+1=a1qn>0,
若a1>0,则qn>0(n∈N*),即q>0;
若a1<0,则qn<0(n∈N*),不存在.
所以甲是乙的必要条件.
7.(2021·浙江)已知多项式(x-1)3+(x+1)4=x4+a1x3+a2x2+a3x+a4,则a1=____,a2+a3+a4=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5
10
令x=1时,则有1+a1+a2+a3+a4=24=16,
所以a2+a3+a4=16-5-1=10.
8.(2017·北京)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:
(1)男学生人数多于女学生人数;
(2)女学生人数多于教师人数;
(3)教师人数的两倍多于男学生人数.
①若教师人数为4,则女学生人数的最大值为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6
解析 若教师人数为4,
则男学生人数小于8,最大值为7,女学生人数最大时应比男学生人数少1人,
所以女学生人数的最大值为7-1=6.
②该小组人数的最小值为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12
解析 设男学生人数为x(x∈N*),要求该小组人数的最小值,
则女学生人数为x-1,教师人数为x-2.
又2(x-2)>x,解得x>4,即x=5,
该小组人数的最小值为5+4+3=12.
9.(2021·北京房山区模拟)已知a,b∈R,且a>b,则下列各式中一定成立的是
A. B.a3>b3
C.ab>b2 D.2|a|>2|b|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模拟精选
√
解析 因为a,b∈R,且a>b,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,因为函数y=x3在定义域R上单调递增,
所以a3>b3,故B正确;
对于C,若b=0,
则ab=b2=0,故C错误;
对于D,若a=1,b=-1,
则2|a|=2|b|,故D错误.
A.20 B.15
C.9 D.6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设四边形ABCD为矩形,建系如图,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
函数f(x)为奇函数,排除BC选项;
所以f(x)<0,排除D选项.
故过P,Q,C三点的截面把棱柱分成的两部分体积之比为2∶1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.如图,在棱柱的侧棱A1A和B1B上各有一动点P,Q满足A1P=BQ,过P,Q,C三点的截面把棱柱分成两部分,则其体积之比为
A.3∶1 B.2∶1
C.4∶1 D.
√
解析 令P与A1重合,Q与B重合,
此时A1P=BQ=0,
则 ,
13.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.2 B.3
C.-3 D.-4
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
且x→+∞时,t→0,
∴只需关于t的方程(m+2)t2-2mt+1=0(*)有且只有一个正实根.
15.若(2x+4)2n=a0+a1x+a2x2+…+a2nx2n(n∈N*),则a2+a4+…+a2n被3除的余数是__.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
解析 令x=0,得a0=42n.
分别令x=1和x=-1,将得到的两式相加,
被3除的余数是1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.现有灰色与白色的卡片各八张,分别写有数字1到8.甲、乙、丙、丁四个人每人面前摆放四张,并按从小到大的顺序自左向右排列(当灰色卡片和白色卡片数字相同时,白色卡片摆在灰色卡片的右侧).如图,甲面前的四张卡片已经翻开,则写有数字4的灰色卡片是___.(填写字母)
K
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得E=1,J=2,L=8,
假设H=4,则F=3,G=4,
此时白色的“4”在灰色的“4”的左边,
不符合题意,所以假设不成立.
假设K=4,则由题意得
白2,灰3,白7,灰8;灰1,白5,白6,灰7;
白1,灰2,灰4,白8;白3,白4,灰5,灰6.
故K=4时,符合题意.
考情分析
练后疑难精讲
高考数学选择题主要考查对基础知识的理解、基本技能的熟练程度、基本计算的准确性、基本方法的正确运用、考虑问题的严谨、解题速度的快捷等方面,注重多个知识点的小型综合,渗透各种数学思想和方法,能充分考查灵活应用基础知识解决数学问题的能力.
一、特(例)值法
核心提炼
从题干(或选项)出发,通过选取符合条件的特殊情况(特殊值、特殊点、特殊位置、特殊函数等)代入,将问题特殊化或构造满足题设条件的特殊函数或图形位置进行判断.特殊化法是“小题小做”的重要策略.
题号 2 6 7 8 9 10 12 15
二、排除法
核心提炼
排除法(淘汰法)是充分利用单项选择题有且只有一个正确的选项这一特征,通过分析、推理、计算、判断,排除不符合要求的选项,从而得出正确结论的一种方法.
题号 3 4 11 13
三、验证法
核心提炼
验证法从题设条件出发,运用有关概念、性质、定理、法则和公式等知识,逐一检验选项得出答案.
题号 1 5 14 16
1
2
3
4
5
易错对点精补
6
1.[T1补偿](2021·平顶山模拟)已知数列{an}的前n项和为Sn,Sn=n2an,a1=1,则Sn等于
√
2.[T9补偿](2021·信阳模拟)对于任意非零实数a,b,且a>b,又c∈R,则有
A.lg(a-b)>0 B.ac2
1
2
3
4
5
√
6
解析 当a=2,b=1时,lg(a-b)=0,故A错误;
当c=0时,ac2=bc2,故B错误;
当a=1,b=-1时,a2=b2,故C错误;
1
2
3
4
5
3.[T3补偿](2021·常州模拟)函数f(x)=sin x· 的图象大致是
6
√
1
2
3
4
5
6
可得f(0)=0,可排除B,C选项;
所以函数f(x)为偶函数,所以排除D选项.
1
2
3
4
5
6
A.36 B.24 C.18 D.12
√
解析 取特殊函数,根据条件可设f(x)=3x,
1
2
3
4
5
6
√
1
2
3
4
5
解析 因为函数f(x)的最小值为-2+1=-1,
由函数f(x)的图象与直线y=-1相邻两个交点的距离为π可得,
该函数的最小正周期为T=π,
6
故f(x)=2sin(2x+φ)+1.
由f(x)>1,可得sin(2x+φ)>0.
1
2
3
4
5
6
6.[T12补偿]如图,在三棱锥O—ABC中,三条棱OA,OB,OC两两垂直,且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3的大小关系为________.
1
2
3
4
5
6
S3
则需满足与截面对应的交点E,F,G分别为中点即可.
故可以将三条棱长分别取为OA=6,OB=4,OC=2,如图,
1
2
3
4
5
6
故S3
同课章节目录
