第2部分 专题1 第1讲 三角函数的图象与性质(共65张PPT)
文档属性
| 名称 | 第2部分 专题1 第1讲 三角函数的图象与性质(共65张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 20:47:56 | ||
图片预览










文档简介
(共65张PPT)
专题一 三角函数与解三角形
第二部分 核心专题 师生共研
第1讲 三角函数的图象与性质
考点1 三角函数的值域、最值
01
高考串讲·找规律
考题变迁·提素养
考点2 三角函数的图象与解析式
02
高考串讲·找规律
考题变迁·提素养
考点3 三角函数的性质及应用
03
高考串讲·找规律
考题变迁·提素养
第二部分
核心专题
师生共研
【解密高考·融会贯通
二轮复习的核心是把所学知识系统化、条理化、综合化,重点突破薄
弱环节
为帮助同学们节约时间,更好地把握高考命题特点,提炼高考命题考
查点,我们划分七大专题,通过研究高考题,把握命题规律,全方位提升
解题能力每个专题最后设置“审题与答题示范”,让学生更加了解高考、
读懂高考、战胜高考:
◇剖解题干,挖掘关键信息一“四字解题”,构建思维导图
◇细研过程,规范答题步骤一优化解析、赋分值、批注关键技法
两角和与差的正弦、余弦、正切公式《
sin(a±B)=sin acos B±cos asin B.
cos(a±B)=cos acos B干sin asin B.
tan(a±B)=
tana±tanB
1千tan atan B
sin(ax+B)sin(a-B)=sin2a-sin2B(平方正弦公式).
cos(a+B)cos(a-B)=cos2 a-sin2 B.
三角函数的概念、诱导公式及同角关系《
)二倍角公式、辅助角公式
(1)二倍角公式
(1)三角函数:设α是一个任意角,它的终边与单位
sin 2 a=2sin acos a.
圆交于点Pk,,则sina=y,c0sa=x,iama=.各
cos 2 a=cos2 a-sin2 a=2cos2 a-1=1-2sin2 a.
2tan a
象限角的三角函数值的符号:一全正,二正弦,
tan 2a=1-tan a
三正切,四余弦、
D1+sin 2a=(sin a+cos a)2.
21-sin 2q=(sin a-cos a)2.
(②同角关系:sina+eos2a-1,0
-=tan a.
(2)辅助角公式
()诱导公式:在+,k∈Z的诱导公式中“奇变
建
y=asin x+bcos x=a2+62 (sin xcos p+cos xsin p)=/a2462.
sin(x+p,其中角p的终边所在象限由a,b的符号确定,
偶不变,符号看象限”.
角o的值由an9=名(a≠0确定
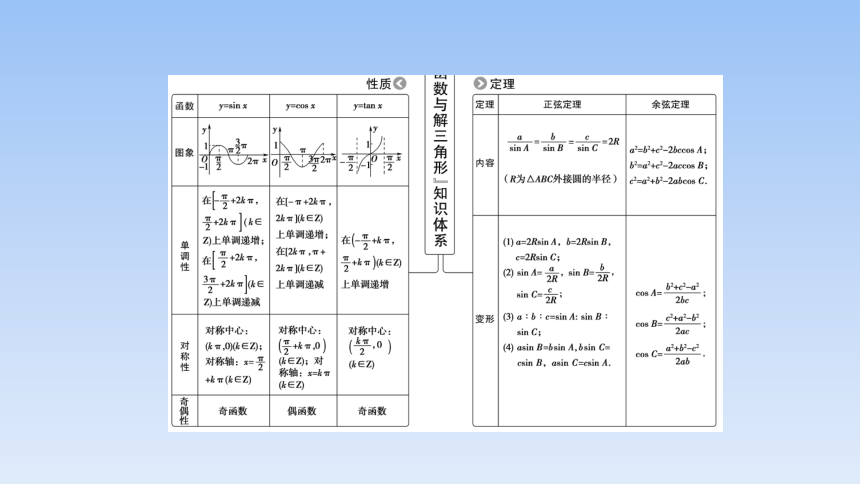
性质
)定理
函数
y=sin x
y=cos x
y=tan x
角函数与解三角形
定理
正弦定理
余弦定理
a
b
=2R
图象
17
sin A sin B sin C
a2=62+c2-2bccos A;
9
2
02m
内容
2
b2=a2+c2-2accos B;
(R为△ABC外接圆的半径)
c2=a2+62-2abcos C.
在罗+2km,
在[-T+2kT,
变+2km](k∈
2hT]k∈Z )
上单调递增;
Z)上单调递增;
在[2kT,T+
在(受·
知识体系
(1)a=2Rsin A,b=2Rsin B,
调
c=2Rsin C;
2kT]k∈Z)
受+6m讴e乙
3m+2kmk∈
上单调递减
上单调递增
②sm4汉imB=R
Z)上单调递减
sin C-
cos A=bitc -a2
2bc
变形
(3)a:b:c=sin A:sin B:
对称中心:
对称中心:
Cos B=c2+a2-62
对称中心:
sin C;
2ac
对
(kT,0k∈Z):
+kT,0】
2
(,0】
(4)asin B=bsin A,bsin C=
对称轴:=受
(作∈Z);对
COs C=a2+62-c2
性
(k∈Z)
csin B,asin C=csin A.
2ab
称轴:x=kT
+kT(k∈Z)
(k∈Z)
奇
奇函数
偶函数
奇函数
专题一 三角函数与解三角形
第二部分 核心专题 师生共研
第1讲 三角函数的图象与性质
考点1 三角函数的值域、最值
01
高考串讲·找规律
考题变迁·提素养
考点2 三角函数的图象与解析式
02
高考串讲·找规律
考题变迁·提素养
考点3 三角函数的性质及应用
03
高考串讲·找规律
考题变迁·提素养
第二部分
核心专题
师生共研
【解密高考·融会贯通
二轮复习的核心是把所学知识系统化、条理化、综合化,重点突破薄
弱环节
为帮助同学们节约时间,更好地把握高考命题特点,提炼高考命题考
查点,我们划分七大专题,通过研究高考题,把握命题规律,全方位提升
解题能力每个专题最后设置“审题与答题示范”,让学生更加了解高考、
读懂高考、战胜高考:
◇剖解题干,挖掘关键信息一“四字解题”,构建思维导图
◇细研过程,规范答题步骤一优化解析、赋分值、批注关键技法
两角和与差的正弦、余弦、正切公式《
sin(a±B)=sin acos B±cos asin B.
cos(a±B)=cos acos B干sin asin B.
tan(a±B)=
tana±tanB
1千tan atan B
sin(ax+B)sin(a-B)=sin2a-sin2B(平方正弦公式).
cos(a+B)cos(a-B)=cos2 a-sin2 B.
三角函数的概念、诱导公式及同角关系《
)二倍角公式、辅助角公式
(1)二倍角公式
(1)三角函数:设α是一个任意角,它的终边与单位
sin 2 a=2sin acos a.
圆交于点Pk,,则sina=y,c0sa=x,iama=.各
cos 2 a=cos2 a-sin2 a=2cos2 a-1=1-2sin2 a.
2tan a
象限角的三角函数值的符号:一全正,二正弦,
tan 2a=1-tan a
三正切,四余弦、
D1+sin 2a=(sin a+cos a)2.
21-sin 2q=(sin a-cos a)2.
(②同角关系:sina+eos2a-1,0
-=tan a.
(2)辅助角公式
()诱导公式:在+,k∈Z的诱导公式中“奇变
建
y=asin x+bcos x=a2+62 (sin xcos p+cos xsin p)=/a2462.
sin(x+p,其中角p的终边所在象限由a,b的符号确定,
偶不变,符号看象限”.
角o的值由an9=名(a≠0确定
性质
)定理
函数
y=sin x
y=cos x
y=tan x
角函数与解三角形
定理
正弦定理
余弦定理
a
b
=2R
图象
17
sin A sin B sin C
a2=62+c2-2bccos A;
9
2
02m
内容
2
b2=a2+c2-2accos B;
(R为△ABC外接圆的半径)
c2=a2+62-2abcos C.
在罗+2km,
在[-T+2kT,
变+2km](k∈
2hT]k∈Z )
上单调递增;
Z)上单调递增;
在[2kT,T+
在(受·
知识体系
(1)a=2Rsin A,b=2Rsin B,
调
c=2Rsin C;
2kT]k∈Z)
受+6m讴e乙
3m+2kmk∈
上单调递减
上单调递增
②sm4汉imB=R
Z)上单调递减
sin C-
cos A=bitc -a2
2bc
变形
(3)a:b:c=sin A:sin B:
对称中心:
对称中心:
Cos B=c2+a2-62
对称中心:
sin C;
2ac
对
(kT,0k∈Z):
+kT,0】
2
(,0】
(4)asin B=bsin A,bsin C=
对称轴:=受
(作∈Z);对
COs C=a2+62-c2
性
(k∈Z)
csin B,asin C=csin A.
2ab
称轴:x=kT
+kT(k∈Z)
(k∈Z)
奇
奇函数
偶函数
奇函数
同课章节目录
