第2部分 专题5 第1讲 直线与圆 课件(共33张PPT)
文档属性
| 名称 | 第2部分 专题5 第1讲 直线与圆 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 14:07:13 | ||
图片预览










文档简介
(共51张PPT)
专题五 解析几何
第1讲 直线与圆
第二部分 核心专题 师生共研
考点1 直线的方程及应用
01
高考串讲·找规律
考题变迁·提素养
考点2 圆的方程及应用
02
高考串讲·找规律
考题变迁·提素养
考点3 直线与圆的位置关系
03
高考串讲·找规律
考题变迁·提素养
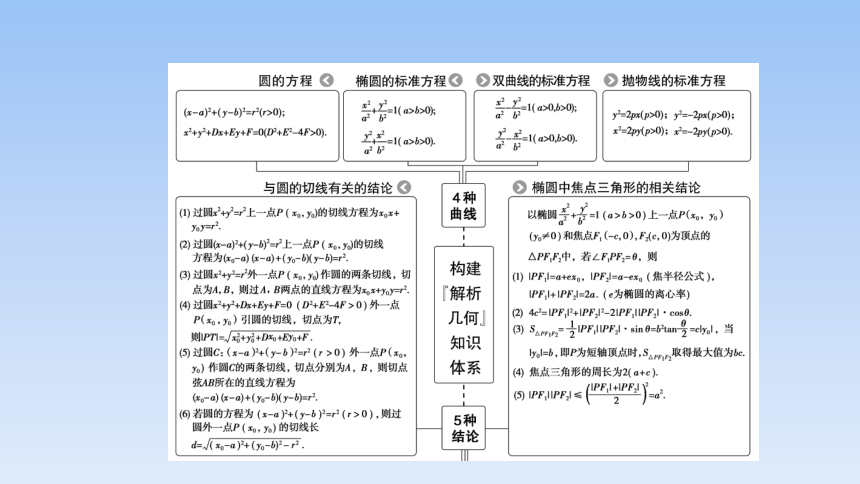
圆的方程
椭圆的标准方程
)双曲线的标准方程
)抛物线的标准方程
(x-a)2+(y-b)2=r2(r>0);
2+y=1(a>b>0射
2y-1(>0,b6>0好
a2'b2
a2 b2
y2=2px(p>0);y2=-2px(p>0);
x2+y2+Dx+Ey+F=0(D2+2-4F>0):
Y女=1(a>b>0.
y2_岁=1(a>0,b>0).
x2=2py(p>0);x2=-2py(p>0).
a2 b2
a2 b2
与圆的切线有关的结论
椭圆中焦点三角形的相关结论
4种
(1)过圆x+y2=2上一点P(xo,yo)的切线方程为xox+
曲线
Yoy=r2.
以睛回手+书(a6>0上一点,
(yo≠0)和焦点F,(-c,0),F2(c,0)为顶点的
②)过圆(x-2+(y-b)2=r2上一点P(x0,yo的切线
方程为(x。-a)(x-a)+(yo-bXy-b)=r2.
△PFF中,若∠FPF2=0,则
3)过圆x2+y2=T外一点P(,y)作圆的两条切线,切
构建
(1)IPF,l=a+exo,IPF2l=a-ex0(焦半径公式),
点为A,B,则过A,B两点的直线方程为xx+yoy=r2
『解析
lPFl+lPF,l=2a.(e为椭圆的离心率)
(4过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点
P(x,)引圆的切线,切点为T
几何
(2)4c2-IPF 12+IPF212-2IPF IIPF2I cos0.
0
则1PT=√J好+y+Dx+Eyo+F.
(3)S。号PFIPF,·sin0=bar号-cbol,当
知识
(⑤)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(xo,
yol=b,即P为短轴顶点时,Sarr,取得最大值为bc,
)作圆C的两条切线,切点分别为A,B,则切点
体系
(4)焦点三角形的周长为2(a+c).
弦AB所在的直线方程为
(o-a)(x-a)+(yo-b(y-b)=r2.
2
(⑥若圆的方程为(x-a)2+(y-b)2=r2(r>0),则过
圆外一点P(xo,y0)的切线长
5种
结论
d=(xo-a)2+(Yo-6)2-r2.
双曲线的方程与渐近线方程的关系《
①双曲线常用的结论
◇抛物线焦点弦的相关结论
山若双面线的方程为层茶-1
(1)双曲线的焦点到其渐近线的距离为b.
设AB是过抛物线y2=2px(p>0)
(②)若P是双曲线右支上一点,F,F2分别为双曲线
的焦点F的弦,若A(x1,y),B(,
(a>0,b>0),则渐近线的方程为
的左、右焦点,则PF=a+c,PFla=c-a.
1),a为直线AB的倾斜角.则
x2 y2
于=0,即y=±2x
③)同支的焦点弦中最短的为通径(过焦点且垂直于
长轴的弦),其长为,异支的弦中最短的为实
()焦半径AF=x1+2=1-cosa
(2)若渐近线的方程为)=±会x(a>0,
p
轴,其长为2a.
6>0),即总±名0,则双曲线
BF1=x2+2=1+c0sm
a
(4)P是双曲线上不同于实轴两顶点的任意一点,F,
的方程可设为芳-入
图羊
F2分别为双曲线的左、右焦点,A,B分别为双曲线
(3)弦长AB到=x1+x2+p=
2p
③)若所求双曲线与双曲线器-茶1
实箱的点,则切票,Se
sin2a
④高+合
12
2
(a>0,b>0)有公共渐近线,其
其中0为∠FPF2
(⑤)以弦AB为直径的圆与准线相切,
方程可设为。茶-入(A0,焦
何P限双尚线若若1(a>0,6>0)右支上不同
于实轴顶点的任意一点,F1,F分别为双曲线的
(⑥SOU2s0d(0为抛物线的
点在x轴上;入<0,焦点在y轴上).
左、右焦点,I为△PFF2内切圆的圆心,则圆心I
顶点)
的横坐标恒为a.
⑨AB是双曲线号京-1o>0,b>0个平行于对称轴
的弦,M(o,o)为AB的中点,则m6=。,即
B如果焦点在轴上,则有k
ayo
b2yo
专题五 解析几何
第1讲 直线与圆
第二部分 核心专题 师生共研
考点1 直线的方程及应用
01
高考串讲·找规律
考题变迁·提素养
考点2 圆的方程及应用
02
高考串讲·找规律
考题变迁·提素养
考点3 直线与圆的位置关系
03
高考串讲·找规律
考题变迁·提素养
圆的方程
椭圆的标准方程
)双曲线的标准方程
)抛物线的标准方程
(x-a)2+(y-b)2=r2(r>0);
2+y=1(a>b>0射
2y-1(>0,b6>0好
a2'b2
a2 b2
y2=2px(p>0);y2=-2px(p>0);
x2+y2+Dx+Ey+F=0(D2+2-4F>0):
Y女=1(a>b>0.
y2_岁=1(a>0,b>0).
x2=2py(p>0);x2=-2py(p>0).
a2 b2
a2 b2
与圆的切线有关的结论
椭圆中焦点三角形的相关结论
4种
(1)过圆x+y2=2上一点P(xo,yo)的切线方程为xox+
曲线
Yoy=r2.
以睛回手+书(a6>0上一点,
(yo≠0)和焦点F,(-c,0),F2(c,0)为顶点的
②)过圆(x-2+(y-b)2=r2上一点P(x0,yo的切线
方程为(x。-a)(x-a)+(yo-bXy-b)=r2.
△PFF中,若∠FPF2=0,则
3)过圆x2+y2=T外一点P(,y)作圆的两条切线,切
构建
(1)IPF,l=a+exo,IPF2l=a-ex0(焦半径公式),
点为A,B,则过A,B两点的直线方程为xx+yoy=r2
『解析
lPFl+lPF,l=2a.(e为椭圆的离心率)
(4过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点
P(x,)引圆的切线,切点为T
几何
(2)4c2-IPF 12+IPF212-2IPF IIPF2I cos0.
0
则1PT=√J好+y+Dx+Eyo+F.
(3)S。号PFIPF,·sin0=bar号-cbol,当
知识
(⑤)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(xo,
yol=b,即P为短轴顶点时,Sarr,取得最大值为bc,
)作圆C的两条切线,切点分别为A,B,则切点
体系
(4)焦点三角形的周长为2(a+c).
弦AB所在的直线方程为
(o-a)(x-a)+(yo-b(y-b)=r2.
2
(⑥若圆的方程为(x-a)2+(y-b)2=r2(r>0),则过
圆外一点P(xo,y0)的切线长
5种
结论
d=(xo-a)2+(Yo-6)2-r2.
双曲线的方程与渐近线方程的关系《
①双曲线常用的结论
◇抛物线焦点弦的相关结论
山若双面线的方程为层茶-1
(1)双曲线的焦点到其渐近线的距离为b.
设AB是过抛物线y2=2px(p>0)
(②)若P是双曲线右支上一点,F,F2分别为双曲线
的焦点F的弦,若A(x1,y),B(,
(a>0,b>0),则渐近线的方程为
的左、右焦点,则PF=a+c,PFla=c-a.
1),a为直线AB的倾斜角.则
x2 y2
于=0,即y=±2x
③)同支的焦点弦中最短的为通径(过焦点且垂直于
长轴的弦),其长为,异支的弦中最短的为实
()焦半径AF=x1+2=1-cosa
(2)若渐近线的方程为)=±会x(a>0,
p
轴,其长为2a.
6>0),即总±名0,则双曲线
BF1=x2+2=1+c0sm
a
(4)P是双曲线上不同于实轴两顶点的任意一点,F,
的方程可设为芳-入
图羊
F2分别为双曲线的左、右焦点,A,B分别为双曲线
(3)弦长AB到=x1+x2+p=
2p
③)若所求双曲线与双曲线器-茶1
实箱的点,则切票,Se
sin2a
④高+合
12
2
(a>0,b>0)有公共渐近线,其
其中0为∠FPF2
(⑤)以弦AB为直径的圆与准线相切,
方程可设为。茶-入(A0,焦
何P限双尚线若若1(a>0,6>0)右支上不同
于实轴顶点的任意一点,F1,F分别为双曲线的
(⑥SOU2s0d(0为抛物线的
点在x轴上;入<0,焦点在y轴上).
左、右焦点,I为△PFF2内切圆的圆心,则圆心I
顶点)
的横坐标恒为a.
⑨AB是双曲线号京-1o>0,b>0个平行于对称轴
的弦,M(o,o)为AB的中点,则m6=。,即
B如果焦点在轴上,则有k
ayo
b2yo
同课章节目录
