第2部分 专题7 第1讲 坐标系与参数方程 课件(共40张PPT)
文档属性
| 名称 | 第2部分 专题7 第1讲 坐标系与参数方程 课件(共40张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 17:07:05 | ||
图片预览





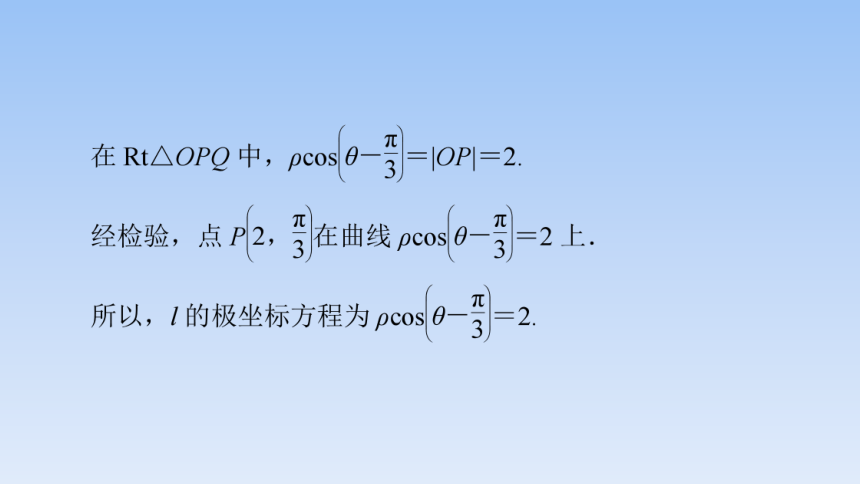






文档简介
(共40张PPT)
专题七 选考部分
第1讲 坐标系与参数方程
第二部分 核心专题 师生共研
考点1 极坐标方程及其应用
01
高考串讲·找规律
考题变迁·提素养
考点2 参数方程及其应用
02
高考串讲·找规律
考题变迁·提素养
极坐标系《
◇不等式选讲
极坐标与直角坐标的互化
绝对值三角不等式
px+",x=pcos 0,y=psin0,tan0-()
(1)定理1:如果a,b是实数,则la+bl≤lal+IbL,当且仅
当ab≥0时,等号成立
直线的极坐标方程
(2)性质:lal-Ibl≤la±b1l≤lal+lbl.
若直线过点M(Po,0。),且此直线与极轴所成的角为a,
(3)定理2:如果a,b,c是实数,那么la-cl≤la-bl+lb-cl,
则它的方程为psin(0-a)=Posin(0。-a).
当且仅当(a-b)(b-c)≥0时,等号成立.
几个特殊位置的直线的极坐标方程:
绝对值不等式的解法
(1)直线过极点:0=0和0=π+0。;
(I)含绝对值的不等式lxla(a>0)的解法:
(2)直线过点M(a,0),且垂直于极轴:pcos0=a;
①Ixl②lxl>a台x>a或x<-a.
(3)直线过M(6,罗),且平行于极轴:psin0=b.
(2)川ax+bl≤c(c>0)和Iax+bl≥c(c>0)型不等式的解法:
圆的极坐标方程
①lax+bl≤c台-c≤ax+b≤c;
若圆心为M(Po,0),半径为r,则圆的方程为p2
②lax+bl≥c台ax+b≥c或ax+b≤-c.
(3)川x-al+lx-bl≥c(c>0)和lx-al+lx-bl≤c(c>0)型不等
2 Po pcos(0-0)+p-r2=0,
式的解法。
几个特殊位置的圆的极坐标方程:
基本不等式
(1)圆心位于极点,半径为r:p=r;
定理1:如果a,b∈R,那么a2+b2≥2ab,当且仅当
(2)圆心位于M(a,0),半径为a:p=2acos0:
a=b时,等号成立.
(3)圆心位于Ma,罗),半径为a:p=2asin0.
考部
定理2:如果a,6>0,那么生步≥a6,当H仪当a=6
时,等号成立.
参数方程
定理3:如果a,6cER,那么+c≥ac,当且
一些常见曲线的参数方程
仅当a=b=c时,等号成立.
(1)过点P(xo,yo),且倾斜角为a的直线的参数方程
定理4:(一般形式的算术一几何平均不等式)对于n个
为x=xo+tco8&,
正数a1,a2,…,an,它们的算术平均不小于它们的几何平
y=yo+-tsin a.'(t为参数)
均,即+a计…+a。≥a44…4,当且仪当
(2)圆的方程(x-a)+(y-b)2=r2的参数方程为
a1=a2==an时,等号成立.
x=a+rcos日,(0为参数)
y=b+rsin 0.
柯西不等式
()精圈方程兰茶-1e咖>0的参数方程为
(1)二维形式的柯西不等式:若a,b,c,d都是实数,则
(a2+b2)(c2+d2)≥(ac+bd)2,当且仅当ad=bc时,等号
x=acos 0,
成立.
ly=bsin 0.
(0为参数)
(2)柯西不等式的向量形式:设α,B是两个向量,则
(4)抛物线方程y2=2px(p>0)的参数方程为
laBl≤IaIB1,当且仅当B是零向量,或存在实数k,
rx=2pt2,
使=kB时,等号成立.
y=2pt.
(t为参数)
(3)二维形式的三角不等式:设x1y1,x2,y2∈R,那么
参数方程的几何意义
、x+y++y≥x1-x2)2+(y-y2)2.
过定点P(xoy),倾斜角为α的直线参数方程的标准形
式为“:为参数:的几何意义是直线上的
(4)一般形式的柯西不等式:设a1,a2,a3,…,an,b1,b2,b3,
…,bn是实数,则(a+a+…+a)b+b+…+b)≥
点P到点P(xoyo)的数量,即Itl=PoPI,t可正可负
(a1b1ta2b2+…+anbn)2,当且仅当b=0(i=1,2,…,n)或存
使用该式时直线上任意两点P1,P对应的参数分别为t1,
在一个数k,使得a=kb,(i=1,2,…,n)时,等号成立.
t2,则1PP2=t1-tl,P1P2的中点对应的参数为号(t1+t2).
专题七 选考部分
第1讲 坐标系与参数方程
第二部分 核心专题 师生共研
考点1 极坐标方程及其应用
01
高考串讲·找规律
考题变迁·提素养
考点2 参数方程及其应用
02
高考串讲·找规律
考题变迁·提素养
极坐标系《
◇不等式选讲
极坐标与直角坐标的互化
绝对值三角不等式
px+",x=pcos 0,y=psin0,tan0-()
(1)定理1:如果a,b是实数,则la+bl≤lal+IbL,当且仅
当ab≥0时,等号成立
直线的极坐标方程
(2)性质:lal-Ibl≤la±b1l≤lal+lbl.
若直线过点M(Po,0。),且此直线与极轴所成的角为a,
(3)定理2:如果a,b,c是实数,那么la-cl≤la-bl+lb-cl,
则它的方程为psin(0-a)=Posin(0。-a).
当且仅当(a-b)(b-c)≥0时,等号成立.
几个特殊位置的直线的极坐标方程:
绝对值不等式的解法
(1)直线过极点:0=0和0=π+0。;
(I)含绝对值的不等式lxl
(2)直线过点M(a,0),且垂直于极轴:pcos0=a;
①Ixl
(3)直线过M(6,罗),且平行于极轴:psin0=b.
(2)川ax+bl≤c(c>0)和Iax+bl≥c(c>0)型不等式的解法:
圆的极坐标方程
①lax+bl≤c台-c≤ax+b≤c;
若圆心为M(Po,0),半径为r,则圆的方程为p2
②lax+bl≥c台ax+b≥c或ax+b≤-c.
(3)川x-al+lx-bl≥c(c>0)和lx-al+lx-bl≤c(c>0)型不等
2 Po pcos(0-0)+p-r2=0,
式的解法。
几个特殊位置的圆的极坐标方程:
基本不等式
(1)圆心位于极点,半径为r:p=r;
定理1:如果a,b∈R,那么a2+b2≥2ab,当且仅当
(2)圆心位于M(a,0),半径为a:p=2acos0:
a=b时,等号成立.
(3)圆心位于Ma,罗),半径为a:p=2asin0.
考部
定理2:如果a,6>0,那么生步≥a6,当H仪当a=6
时,等号成立.
参数方程
定理3:如果a,6cER,那么+c≥ac,当且
一些常见曲线的参数方程
仅当a=b=c时,等号成立.
(1)过点P(xo,yo),且倾斜角为a的直线的参数方程
定理4:(一般形式的算术一几何平均不等式)对于n个
为x=xo+tco8&,
正数a1,a2,…,an,它们的算术平均不小于它们的几何平
y=yo+-tsin a.'(t为参数)
均,即+a计…+a。≥a44…4,当且仪当
(2)圆的方程(x-a)+(y-b)2=r2的参数方程为
a1=a2==an时,等号成立.
x=a+rcos日,(0为参数)
y=b+rsin 0.
柯西不等式
()精圈方程兰茶-1e咖>0的参数方程为
(1)二维形式的柯西不等式:若a,b,c,d都是实数,则
(a2+b2)(c2+d2)≥(ac+bd)2,当且仅当ad=bc时,等号
x=acos 0,
成立.
ly=bsin 0.
(0为参数)
(2)柯西不等式的向量形式:设α,B是两个向量,则
(4)抛物线方程y2=2px(p>0)的参数方程为
laBl≤IaIB1,当且仅当B是零向量,或存在实数k,
rx=2pt2,
使=kB时,等号成立.
y=2pt.
(t为参数)
(3)二维形式的三角不等式:设x1y1,x2,y2∈R,那么
参数方程的几何意义
、x+y++y≥x1-x2)2+(y-y2)2.
过定点P(xoy),倾斜角为α的直线参数方程的标准形
式为“:为参数:的几何意义是直线上的
(4)一般形式的柯西不等式:设a1,a2,a3,…,an,b1,b2,b3,
…,bn是实数,则(a+a+…+a)b+b+…+b)≥
点P到点P(xoyo)的数量,即Itl=PoPI,t可正可负
(a1b1ta2b2+…+anbn)2,当且仅当b=0(i=1,2,…,n)或存
使用该式时直线上任意两点P1,P对应的参数分别为t1,
在一个数k,使得a=kb,(i=1,2,…,n)时,等号成立.
t2,则1PP2=t1-tl,P1P2的中点对应的参数为号(t1+t2).
同课章节目录
