第1部分 研习4 算法与推理证明 学案(Word版含解析)
文档属性
| 名称 | 第1部分 研习4 算法与推理证明 学案(Word版含解析) | 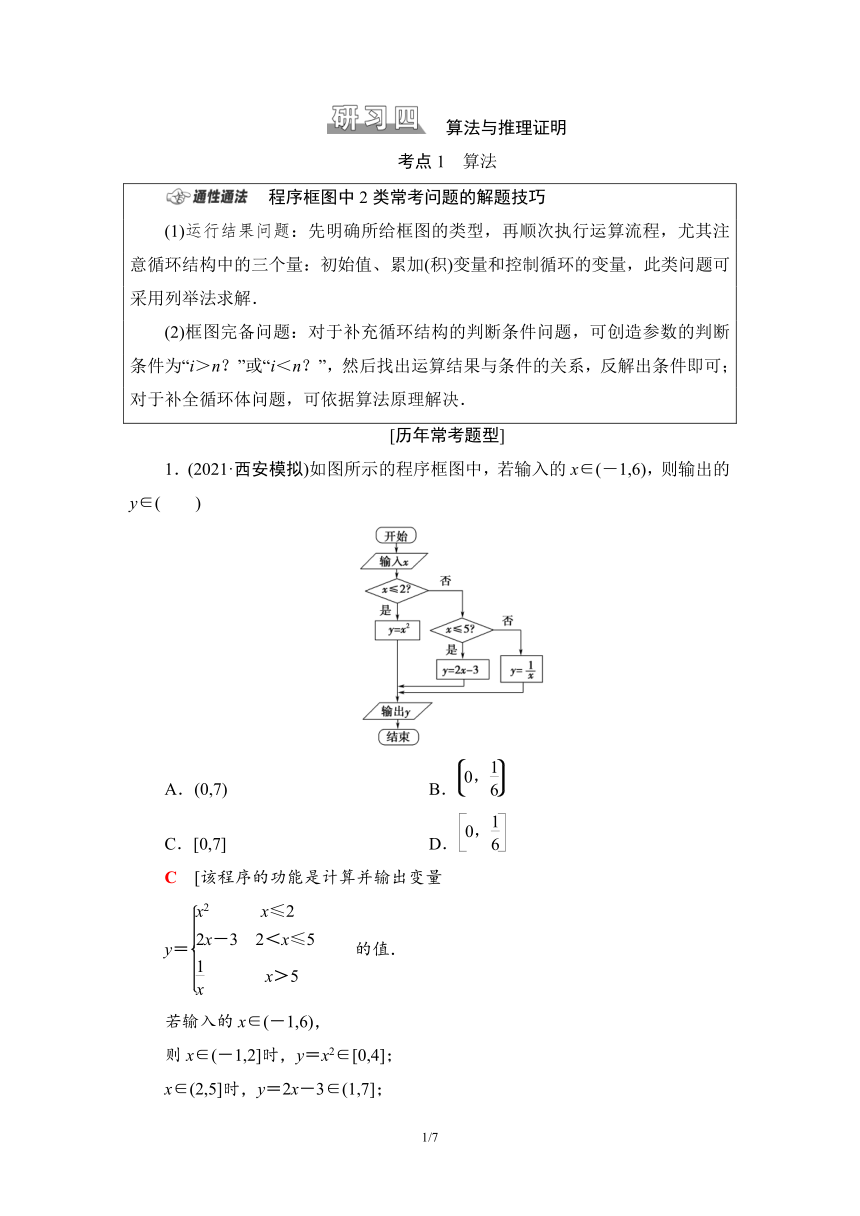 | |
| 格式 | doc | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 07:33:54 | ||
图片预览



文档简介
算法与推理证明
考点1 算法
程序框图中2类常考问题的解题技巧
(1)运行结果问题:先明确所给框图的类型,再顺次执行运算流程,尤其注意循环结构中的三个量:初始值、累加(积)变量和控制循环的变量,此类问题可采用列举法求解.
(2)框图完备问题:对于补充循环结构的判断条件问题,可创造参数的判断条件为“i>n?”或“i<n?”,然后找出运算结果与条件的关系,反解出条件即可;对于补全循环体问题,可依据算法原理解决.
[历年常考题型]
1.(2021·西安模拟)如图所示的程序框图中,若输入的x∈(-1,6),则输出的y∈( )
A.(0,7) B.
C.[0,7] D.
C [该程序的功能是计算并输出变量
y=的值.
若输入的x∈(-1,6),
则x∈(-1,2]时,y=x2∈[0,4];
x∈(2,5]时,y=2x-3∈(1,7];
x∈(5,6)时,y=∈.
综上,输出的y∈[0,7].故选C.]
2.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长三尺,竹长一尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,1,则输出的n=( )
A.5 B.4 C.3 D.2
B [输入的a,b分别为3,1时,执行程序框图得n=1,a=,b=2;n=2,a=,b=4;n=3,a=,b=8;n=4,a=,b=16,
此时a<b,输出n=4.故选B.]
3.(2021·郑州模拟)如图所示程序框图是为了求出满足3n-2n>2 020的最小偶数n,那么在和两个空白框中,可以分别填入( )
A.A>2 020和n=n+1
B.A>2 020和n=n+2
C.A≤2 020和n=n+1
D.A≤2 020和n=n+2
D [因为要求A>2 020时的最小偶数n,且在“否”时输出,所以在“”内不能填入“A>2 020”,而要填入“A≤2 020”.因为要求的n为偶数且n的初始值为0,所以在“”中n依次加2可保证其为偶数,故应填“n=n+2”.故选D.]
4.如图是求的算法框图,图中空白框中应填入( )
A.A=2+ B.A=
C.A= D.A=
C [看最外层根号,知循环体为A=,循环次数为2,验证:
第一步:A=,k=1<3,是,满足条件;
第二步:A=,k=2<3,是,满足条件;
第三步:A=,k=3,否,输出A=,
验证后正确,则A=.故选C.]
[预测创新题型]
5.已知{Fn}是斐波那契数列,则F1=F2=1,Fn=Fn-1+Fn-2(n∈N*且n≥3).如图程序框图表示输出斐波那契数列的前n项的算法,则n=( )
A.10 B.18
C.20 D.22
C [执行程序框图,i=1,a=1,b=1,满足条件,输出斐波那契数列的前2项;a=1+1=2,b=1+2=3,i=2,满足条件,输出斐波那契数列的第3项、第4项;…;每经过一次循环,输出斐波那契数列的2项,i=11时,共输出了斐波那契数列的前20项,此时不满足条件,退出循环体.故n=20.故选C.]
考点2 推理证明
三类推理的解题要点
(1)归纳推理题的3步骤:发现共性、归纳推理、检验结论;
(2)类比推理题的3个关键:定类、类比和检验;
3 逻辑推理的解题绝招:假言判断,即假设一种情况成立或不成立,然后以此为出发点,联系条件,判断是否与题设条件相符合.
[历年常考题型]
1.观察下列各式a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a12+b12=( )
A.322 B.521
C.123 D.199
A [因为a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,等式右边对应的数为1,3,4,7,11,…,所以其规律为从第三项起,每项等于其相邻两项的和.因此,求a12+b12,即是求数列“1,3,4,7,11,…”中的第12项,所以对应的数列为1,3,4,7,11,18,29,47,76,123,199,322”,即第12项为322.]
2.若一个人下半身长(肚脐至足底)与全身长的比近似为,堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好.若某人着装前测得头顶至肚脐长度为72 cm,肚脐至足底长度为103 cm,根据以上数据,作为形象设计师的你,对此人的着装建议是( )
A.身材完美,无需改善
B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋
D.同时穿戴同样高度的增高鞋与帽子
C [因为=≈0.589<0.618,
所以要增加下身长度,
故可以穿一双合适高度的增高鞋.故选C.]
3.某校开设了素描、摄影、剪纸、书法四门选修课,要求每位同学都要选择其中的两门课程.已知甲同学选了素描,乙与甲没有相同的课程,丙与甲恰有一门课程相同,丁与丙没有相同课程.则以下说法错误的是( )
A.丙有可能没有选素描
B.丁有可能没有选素描
C.乙、丁可能两门课都相同
D.这四个人里恰有2个人选素描
C [因为甲选择了素描,所以乙必定没选素描.
那么假设丙选择了素描,则丁一定没选素描;
若丙没选素描,则丁必定选择了素描.
综上,必定有且只有2人选择素描,选项A,B,D判断正确.不妨设甲另一门选修为摄影,则乙素描与摄影均不选择,则对于素描与摄影可能出现如下两种情况:
情形一:
甲 乙 丙 丁
素描 √ × √ ×
摄影 √ × × √
情形二:
甲 乙 丙 丁
素描 √ × × √
摄影 √ × √ ×
由上表可知,乙与丁必有一门课程不相同,因此C不正确.故选C.]
4.在《九章算术》方田章圆田术(刘徽注)中指出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.注述中所用的割圆术是一种无限与有限的转化过程,比如在 中“…”代表无限次重复,但原式却是个定值x,这可以通过方程=x确定出来x=2,类似不难得出1+=________.
[令1+=t(t>0),
由1+=t,解得t=,∵t>0,∴t=.]
[预测创新题型]
5.祖暅(公元5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆+=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图),称为椭球体,课本中介绍了应用祖暅原理求球体体积公式的方法,请类比此法,求出椭球体体积,其体积等于________.
πb2a [椭圆的长半轴长为a,短半轴长为b,现构造两个底面半径为b,高为a的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖暅原理得出椭球体的体积V=2(V圆柱-V圆锥)=2=πb2a.
7/7
考点1 算法
程序框图中2类常考问题的解题技巧
(1)运行结果问题:先明确所给框图的类型,再顺次执行运算流程,尤其注意循环结构中的三个量:初始值、累加(积)变量和控制循环的变量,此类问题可采用列举法求解.
(2)框图完备问题:对于补充循环结构的判断条件问题,可创造参数的判断条件为“i>n?”或“i<n?”,然后找出运算结果与条件的关系,反解出条件即可;对于补全循环体问题,可依据算法原理解决.
[历年常考题型]
1.(2021·西安模拟)如图所示的程序框图中,若输入的x∈(-1,6),则输出的y∈( )
A.(0,7) B.
C.[0,7] D.
C [该程序的功能是计算并输出变量
y=的值.
若输入的x∈(-1,6),
则x∈(-1,2]时,y=x2∈[0,4];
x∈(2,5]时,y=2x-3∈(1,7];
x∈(5,6)时,y=∈.
综上,输出的y∈[0,7].故选C.]
2.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长三尺,竹长一尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,1,则输出的n=( )
A.5 B.4 C.3 D.2
B [输入的a,b分别为3,1时,执行程序框图得n=1,a=,b=2;n=2,a=,b=4;n=3,a=,b=8;n=4,a=,b=16,
此时a<b,输出n=4.故选B.]
3.(2021·郑州模拟)如图所示程序框图是为了求出满足3n-2n>2 020的最小偶数n,那么在和两个空白框中,可以分别填入( )
A.A>2 020和n=n+1
B.A>2 020和n=n+2
C.A≤2 020和n=n+1
D.A≤2 020和n=n+2
D [因为要求A>2 020时的最小偶数n,且在“否”时输出,所以在“”内不能填入“A>2 020”,而要填入“A≤2 020”.因为要求的n为偶数且n的初始值为0,所以在“”中n依次加2可保证其为偶数,故应填“n=n+2”.故选D.]
4.如图是求的算法框图,图中空白框中应填入( )
A.A=2+ B.A=
C.A= D.A=
C [看最外层根号,知循环体为A=,循环次数为2,验证:
第一步:A=,k=1<3,是,满足条件;
第二步:A=,k=2<3,是,满足条件;
第三步:A=,k=3,否,输出A=,
验证后正确,则A=.故选C.]
[预测创新题型]
5.已知{Fn}是斐波那契数列,则F1=F2=1,Fn=Fn-1+Fn-2(n∈N*且n≥3).如图程序框图表示输出斐波那契数列的前n项的算法,则n=( )
A.10 B.18
C.20 D.22
C [执行程序框图,i=1,a=1,b=1,满足条件,输出斐波那契数列的前2项;a=1+1=2,b=1+2=3,i=2,满足条件,输出斐波那契数列的第3项、第4项;…;每经过一次循环,输出斐波那契数列的2项,i=11时,共输出了斐波那契数列的前20项,此时不满足条件,退出循环体.故n=20.故选C.]
考点2 推理证明
三类推理的解题要点
(1)归纳推理题的3步骤:发现共性、归纳推理、检验结论;
(2)类比推理题的3个关键:定类、类比和检验;
3 逻辑推理的解题绝招:假言判断,即假设一种情况成立或不成立,然后以此为出发点,联系条件,判断是否与题设条件相符合.
[历年常考题型]
1.观察下列各式a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a12+b12=( )
A.322 B.521
C.123 D.199
A [因为a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,等式右边对应的数为1,3,4,7,11,…,所以其规律为从第三项起,每项等于其相邻两项的和.因此,求a12+b12,即是求数列“1,3,4,7,11,…”中的第12项,所以对应的数列为1,3,4,7,11,18,29,47,76,123,199,322”,即第12项为322.]
2.若一个人下半身长(肚脐至足底)与全身长的比近似为,堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好.若某人着装前测得头顶至肚脐长度为72 cm,肚脐至足底长度为103 cm,根据以上数据,作为形象设计师的你,对此人的着装建议是( )
A.身材完美,无需改善
B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋
D.同时穿戴同样高度的增高鞋与帽子
C [因为=≈0.589<0.618,
所以要增加下身长度,
故可以穿一双合适高度的增高鞋.故选C.]
3.某校开设了素描、摄影、剪纸、书法四门选修课,要求每位同学都要选择其中的两门课程.已知甲同学选了素描,乙与甲没有相同的课程,丙与甲恰有一门课程相同,丁与丙没有相同课程.则以下说法错误的是( )
A.丙有可能没有选素描
B.丁有可能没有选素描
C.乙、丁可能两门课都相同
D.这四个人里恰有2个人选素描
C [因为甲选择了素描,所以乙必定没选素描.
那么假设丙选择了素描,则丁一定没选素描;
若丙没选素描,则丁必定选择了素描.
综上,必定有且只有2人选择素描,选项A,B,D判断正确.不妨设甲另一门选修为摄影,则乙素描与摄影均不选择,则对于素描与摄影可能出现如下两种情况:
情形一:
甲 乙 丙 丁
素描 √ × √ ×
摄影 √ × × √
情形二:
甲 乙 丙 丁
素描 √ × × √
摄影 √ × √ ×
由上表可知,乙与丁必有一门课程不相同,因此C不正确.故选C.]
4.在《九章算术》方田章圆田术(刘徽注)中指出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.注述中所用的割圆术是一种无限与有限的转化过程,比如在 中“…”代表无限次重复,但原式却是个定值x,这可以通过方程=x确定出来x=2,类似不难得出1+=________.
[令1+=t(t>0),
由1+=t,解得t=,∵t>0,∴t=.]
[预测创新题型]
5.祖暅(公元5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆+=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图),称为椭球体,课本中介绍了应用祖暅原理求球体体积公式的方法,请类比此法,求出椭球体体积,其体积等于________.
πb2a [椭圆的长半轴长为a,短半轴长为b,现构造两个底面半径为b,高为a的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖暅原理得出椭球体的体积V=2(V圆柱-V圆锥)=2=πb2a.
7/7
同课章节目录
