第2部分 专题5 第1讲 直线与圆
文档属性
| 名称 | 第2部分 专题5 第1讲 直线与圆 |  | |
| 格式 | doc | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 23:21:01 | ||
图片预览




文档简介
直线与圆
考点1 直线的方程及应用
1.(2020·全国卷Ⅲ)点(0,-1)到直线y=k(x+1)距离的最大值为( )
A.1 B. C. D.2
B [法一:由点到直线的距离公式知点(0,-1)到直线y=k(x+1)的距离d====.当k=0时,d=1;当k≠0时,d==,要使d最大,需k>0且k+最小,∴当k=1时,dmax=,故选B.
法二:记点A(0,-1),直线y=k(x+1)恒过点B(-1,0),当AB垂直于直线y=k(x+1)时,点A(0,-1)到直线y=k(x+1)的距离最大,且最大值为|AB|=,故选B.]
2.(2021·全国卷乙)双曲线-=1的右焦点到直线x+2y-8=0的距离为________.
[由双曲线的性质知c2=a2+b2=4+5=9,则c=3,双曲线右焦点的坐标为(3,0),所以双曲线的右焦点到直线x+2y-8=0的距离d==.]
命题规律:考查重点是直线间的平行和垂直的应用、与距离、最值有关的问题,此类问题难度属于中低档,一般以选择题、填空题的形式出现.
通性通法:求直线方程的方法
求直线方程主要有直接法和待定系数法.直接法是选择适当的形式,直接求出直线方程.待定系数法通常先由条件建立含参数的方程,再将条件代入求参数,即可得到直线方程.
提醒:求直线方程时应根据条件选择合适的方程形式利用待定系数法求解,同时要验证与x、y轴垂直的特殊情况.
1.[与充分必要条件交汇]已知直线l1:x+(m+1)y+m=0,l2:mx+2y+1=0,则“l1∥l2”的必要不充分条件是( )
A.m=-2 B.m=1
C.m=-2或m=1 D.m=2或m=1
C [∵直线l1:x+(m+1)y+m=0,l2:mx+2y+1=0,若l1∥l2,则m(m+1)-2=0,解得m=-2或m=1;当m=1时,l1与l2重合,故“l1∥l2” “m=-2”,
故“l1∥l2”的必要不充分条件是“m=-2或m=1”,故选C.]
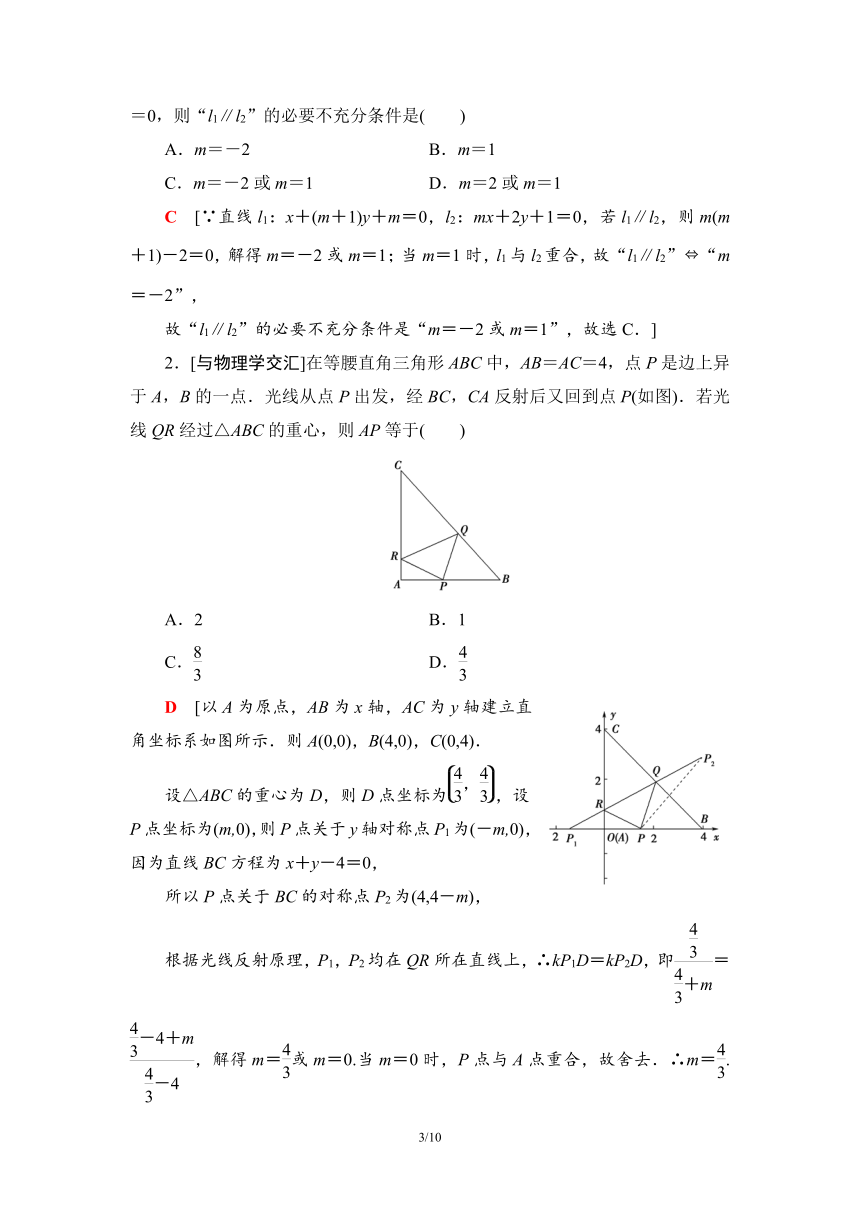
2.[与物理学交汇]在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
A.2 B.1
C. D.
D [以A为原点,AB为x轴,AC为y轴建立直角坐标系如图所示.则A(0,0),B(4,0),C(0,4).
设△ABC的重心为D,则D点坐标为,设P点坐标为(m,0),则P点关于y轴对称点P1为(-m,0),因为直线BC方程为x+y-4=0,
所以P点关于BC的对称点P2为(4,4-m),
根据光线反射原理,P1,P2均在QR所在直线上,∴kP1D=kP2D,即=,解得m=或m=0.当m=0时,P点与A点重合,故舍去.∴m=.故选D.]
3.[与不等式交汇]已知直线l1:kx-y+4=0与直线l2:x+ky-3=0(k≠0)分别过定点A,B,又l1,l2相交于点M,则|MA|·|MB|的最大值为________.
[由题意可知,直线l1:kx-y+4=0经过定点A(0,4),直线l2:x+ky-3=0经过定点B(3,0).
易知直线l1:kx-y+4=0和直线l2:x+ky-3=0始终垂直,又M是两条直线的交点,所以MA⊥MB,
所以|MA|2+|MB|2=|AB|2=25,故|MA|·|MB|≤.]
考点2 圆的方程及应用
1.(2020·全国卷Ⅱ)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线2x-y-3=0的距离为( )
A. B.
C. D.
B [因为圆与两坐标轴都相切,点(2,1)在该圆上,所以可设该圆的方程为(x-a)2+(y-a)2=a2(a>0),所以(2-a)2+(1-a)2=a2,即a2-6a+5=0,解得a=1或a=5,所以圆心的坐标为(1,1)或(5,5),所以圆心到直线2x-y-3=0的距离为=或=,故选B.]
2.(2018·天津高考)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为________.
x2+y2-2x=0 [法一:设圆的方程为x2+y2+Dx+Ey+F=0.
∵圆经过点(0,0),(1,1),(2,0),
∴
解得
∴圆的方程为x2+y2-2x=0.
法二:画出示意图如图所示,
则△OAB为等腰直角三角形,
故所求圆的圆心为(1,0),半径为1,
∴所求圆的方程为(x-1)2+y2=1,
即x2+y2-2x=0.]
命题规律:圆的方程求法以待定系数法为主,主要考查方程思想及数学运算的能力,属于中档题目.
通性通法: 解决圆的方程问题一般有两种方法
(1)几何法:通过研究圆的性质、直线与圆、圆与圆的位置关系,进而求得圆的基本量和方程.
(2)代数法:即用待定系数法先设出圆的方程,再由条件求得各系数.
1.[以阿波罗尼圆为载体]古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”.现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个特定的三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4 km,丙、甲两地距离是丙、乙两地距离的倍,则这个三角形信号覆盖区域的最大面积(单位:km2)是( )
A.2 B.4
C.3 D.4
B [以甲、乙两地所在直线为x轴,线段甲乙的垂直平分线为y轴建立平面直角坐标系(图略),设甲、乙两地的坐标分别为(-2,0),(2,0),丙地坐标为(x,y)(y≠0),则=·,整理得(x-4)2+y2=12,可知丙地所在的圆的半径为r=2.所以三角形信号覆盖区域的最大面积为×4×2=4.]
2.[与圆锥曲线交汇]已知A,B分别是双曲线C:-=1的左、右顶点,P(3,4)为C上一点,则△PAB的外接圆的标准方程为________.
x2+(y-3)2=10 [∵P(3,4)为C上一点,∴-=1,
解得m=1,则B(1,0),∴kPB==2,
PB的中点坐标为(2,2),
PB的中垂线方程为y=-(x-2)+2,
令x=0,则y=3,
设外接圆圆心为M(0,t),
则M(0,3),r=|MB|==,
∴△PAB外接圆的标准方程为x2+(y-3)2=10.]
3.[由圆的一般方程求参数(或范围)](2021·珠海一模)若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则k的取值范围为________.
(-∞,1)∪(4,+∞) [根据题意,若方程
x2+y2+λxy+2kx+4y+5k+λ=0表示圆,
则λ=0,方程为x2+y2+2kx+4y+5k=0,
即(x+k)2+(y+2)2=k2-5k+4,
必有k2-5k+4>0,解得k<1或k>4,
即k的取值范围为(-∞,1)∪(4,+∞).]
考点3 直线与圆的位置关系
1.(2021·新高考卷Ⅰ改编)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则下列结论成立的是( )
①点P到直线AB的距离小于10;
②点P到直线AB的距离大于2;
③当∠PBA最小时,|PB|=3;
④当∠PBA最大时,|PB|=3.
A.①② B.②③
C.②③④ D.①③④
D [设圆(x-5)2+(y-5)2=16的圆心为M(5,5),由题易知直线AB的方程为+=1,即x+2y-4=0,则圆心M到直线AB的距离d==>4,所以直线AB与圆M相离,所以点P到直线AB的距离的最大值为4+d=4+,4+<5+=10,故①正确.
易知点P到直线AB的距离的最小值为d-4=-4,-4<-4=1,故②不正确.
过点B作圆M的两条切线,切点分别为N,Q,如图所示,连接MB,MN,MQ,则当∠PBA最小时,点P与N重合,|PB|===3,当∠PBA最大时,点P与Q重合,|PB|=3,故③④都正确.综上,选D.
]
2.(2020·全国卷Ⅰ)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点.过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
D [法一:由⊙M:x2+y2-2x-2y-2=0 ①,
得⊙M:(x-1)2+(y-1)2=4,所以圆心M(1,1).如图,连接AM,BM,易知四边形PAMB的面积为|PM|·|AB|,欲使|PM|·|AB|最小,只需四边形PAMB的面积最小,即只需△PAM的面积最小.因为|AM|=2,所以只需|PA|最小.又|PA|==,所以只需直线2x+y+2=0上的动点P到M的距离最小,其最小值为=,此时PM⊥l,易求出直线PM的方程为x-2y+1=0.由得所以P(-1,0).易知P,A,M,B四点共圆,所以以PM为直径的圆的方程为x2+=,即x2+y2-y-1=0 ②,由①②得,直线AB的方程为2x+y+1=0,故选D.
法二:因为⊙M:(x-1)2+(y-1)2=4,所以圆心M(1,1).
连接AM,BM,易知四边形PAMB的面积为|PM|·|AB|,欲使|PM|·|AB|最小,只需四边形PAMB的面积最小,即只需△PAM的面积最小.因为|AM|=2,所以只需|PA|最小.
又|PA|==,所以只需|PM|最小,此时PM⊥l.因为PM⊥AB,所以l∥AB,所以kAB=-2,排除A,C.
易求出直线PM的方程为x-2y+1=0,由得所以P(-1,0).因为点M到直线x=-1的距离为2,所以直线x=-1过点P且与⊙M相切,所以A(-1,1).因为点A(-1,1)在直线AB上,故排除B.故选D.]
3.(2020·天津高考)已知直线x-y+8=0和圆x2+y2=r2(r>0)相交于A,B两点.若|AB|=6,则r的值为________.
5 [依题意得,圆心(0,0)到直线x-y+8=0的距离d==4,因此r2=d2+=25,又r>0,所以r=5.]
命题规律:以直线与圆的位置关系为切入点,结合圆的几何性质,勾股定理及距离等相关知识考查数形结合及数学运算能力.一般以选择题、填空题的形式出现,知识相对综合,有一定的区分度.
通性通法:解决直线与圆的位置关系问题应关注3点
(1)处理直线与圆的位置关系问题时,主要利用几何法,即利用圆心到直线的距离与半径的大小关系判断,并依据相关几何性质求解.
(2)弦长问题,主要依据弦长的一半、弦心距、半径之间的关系求解.
(3)过圆内一点且垂直于过这点的半径的弦最短.
1.[直线与圆的关系](2021·广东二模)设直线l:y=kx+1(k∈R)与圆C:x2+y2=5,则下列结论正确的为( )
A.l与C可能相离
B.l可能将C的周长平分
C.当k=1时,l被C截得的弦长为
D.l被C截得的最短弦长为4
D [对于A选项,直线l过定点(0,1),且点(0,1)在圆C内,则直线l与圆C必相交,A选项错误;
对于B选项,若直线l将圆C平分,则直线l过原点,此时直线l的斜率不存在,B选项错误;
对于C选项,当k=1时,直线l的方程为x-y+1=0,圆心C到直线l的距离为d=,所以,直线l被C截得的弦长为2eq \r(5-\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(2),2))))=3,C选项错误;
对于D选项,圆心C到直线l的距离为d=≤1,
所以,直线l被C截得的弦长为2≥4,D选项正确.故选D.]
2.[圆与圆的位置关系]若圆x2+y2=4与圆x2+y2+ax+2ay-9=0(a>0)相交,公共弦的长为2,则a=________.
[联立两圆方程
可得公共弦所在直线方程为ax+2ay-5=0,
故圆心(0,0)到直线ax+2ay-5=0的距离为=(a>0).
故2eq \r(22-\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(5),a))))=2,解得a2=,
因为a>0,所以a=.]
3.[切线问题]设P为直线3x-4y+11=0上的动点,过点P作圆C:x2+y2-2x-2y+1=0的两条切线,切点分别为A,B,则四边形PACB的面积的最小值为________.
[圆的标准方程为(x-1)2+(y-1)2=1,圆心为C(1,1),半径为r=1,根据对称性可知,四边形PACB的面积为2S△APC=2×|PA|r=|PA|=,要使四边形PACB的面积最小,则只需|PC|最小,最小值为圆心到直线l:3x-4y+11=0的距离d===2.
所以四边形PACB面积的最小值为==.]
10/10
考点1 直线的方程及应用
1.(2020·全国卷Ⅲ)点(0,-1)到直线y=k(x+1)距离的最大值为( )
A.1 B. C. D.2
B [法一:由点到直线的距离公式知点(0,-1)到直线y=k(x+1)的距离d====.当k=0时,d=1;当k≠0时,d==,要使d最大,需k>0且k+最小,∴当k=1时,dmax=,故选B.
法二:记点A(0,-1),直线y=k(x+1)恒过点B(-1,0),当AB垂直于直线y=k(x+1)时,点A(0,-1)到直线y=k(x+1)的距离最大,且最大值为|AB|=,故选B.]
2.(2021·全国卷乙)双曲线-=1的右焦点到直线x+2y-8=0的距离为________.
[由双曲线的性质知c2=a2+b2=4+5=9,则c=3,双曲线右焦点的坐标为(3,0),所以双曲线的右焦点到直线x+2y-8=0的距离d==.]
命题规律:考查重点是直线间的平行和垂直的应用、与距离、最值有关的问题,此类问题难度属于中低档,一般以选择题、填空题的形式出现.
通性通法:求直线方程的方法
求直线方程主要有直接法和待定系数法.直接法是选择适当的形式,直接求出直线方程.待定系数法通常先由条件建立含参数的方程,再将条件代入求参数,即可得到直线方程.
提醒:求直线方程时应根据条件选择合适的方程形式利用待定系数法求解,同时要验证与x、y轴垂直的特殊情况.
1.[与充分必要条件交汇]已知直线l1:x+(m+1)y+m=0,l2:mx+2y+1=0,则“l1∥l2”的必要不充分条件是( )
A.m=-2 B.m=1
C.m=-2或m=1 D.m=2或m=1
C [∵直线l1:x+(m+1)y+m=0,l2:mx+2y+1=0,若l1∥l2,则m(m+1)-2=0,解得m=-2或m=1;当m=1时,l1与l2重合,故“l1∥l2” “m=-2”,
故“l1∥l2”的必要不充分条件是“m=-2或m=1”,故选C.]
2.[与物理学交汇]在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
A.2 B.1
C. D.
D [以A为原点,AB为x轴,AC为y轴建立直角坐标系如图所示.则A(0,0),B(4,0),C(0,4).
设△ABC的重心为D,则D点坐标为,设P点坐标为(m,0),则P点关于y轴对称点P1为(-m,0),因为直线BC方程为x+y-4=0,
所以P点关于BC的对称点P2为(4,4-m),
根据光线反射原理,P1,P2均在QR所在直线上,∴kP1D=kP2D,即=,解得m=或m=0.当m=0时,P点与A点重合,故舍去.∴m=.故选D.]
3.[与不等式交汇]已知直线l1:kx-y+4=0与直线l2:x+ky-3=0(k≠0)分别过定点A,B,又l1,l2相交于点M,则|MA|·|MB|的最大值为________.
[由题意可知,直线l1:kx-y+4=0经过定点A(0,4),直线l2:x+ky-3=0经过定点B(3,0).
易知直线l1:kx-y+4=0和直线l2:x+ky-3=0始终垂直,又M是两条直线的交点,所以MA⊥MB,
所以|MA|2+|MB|2=|AB|2=25,故|MA|·|MB|≤.]
考点2 圆的方程及应用
1.(2020·全国卷Ⅱ)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线2x-y-3=0的距离为( )
A. B.
C. D.
B [因为圆与两坐标轴都相切,点(2,1)在该圆上,所以可设该圆的方程为(x-a)2+(y-a)2=a2(a>0),所以(2-a)2+(1-a)2=a2,即a2-6a+5=0,解得a=1或a=5,所以圆心的坐标为(1,1)或(5,5),所以圆心到直线2x-y-3=0的距离为=或=,故选B.]
2.(2018·天津高考)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为________.
x2+y2-2x=0 [法一:设圆的方程为x2+y2+Dx+Ey+F=0.
∵圆经过点(0,0),(1,1),(2,0),
∴
解得
∴圆的方程为x2+y2-2x=0.
法二:画出示意图如图所示,
则△OAB为等腰直角三角形,
故所求圆的圆心为(1,0),半径为1,
∴所求圆的方程为(x-1)2+y2=1,
即x2+y2-2x=0.]
命题规律:圆的方程求法以待定系数法为主,主要考查方程思想及数学运算的能力,属于中档题目.
通性通法: 解决圆的方程问题一般有两种方法
(1)几何法:通过研究圆的性质、直线与圆、圆与圆的位置关系,进而求得圆的基本量和方程.
(2)代数法:即用待定系数法先设出圆的方程,再由条件求得各系数.
1.[以阿波罗尼圆为载体]古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”.现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个特定的三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4 km,丙、甲两地距离是丙、乙两地距离的倍,则这个三角形信号覆盖区域的最大面积(单位:km2)是( )
A.2 B.4
C.3 D.4
B [以甲、乙两地所在直线为x轴,线段甲乙的垂直平分线为y轴建立平面直角坐标系(图略),设甲、乙两地的坐标分别为(-2,0),(2,0),丙地坐标为(x,y)(y≠0),则=·,整理得(x-4)2+y2=12,可知丙地所在的圆的半径为r=2.所以三角形信号覆盖区域的最大面积为×4×2=4.]
2.[与圆锥曲线交汇]已知A,B分别是双曲线C:-=1的左、右顶点,P(3,4)为C上一点,则△PAB的外接圆的标准方程为________.
x2+(y-3)2=10 [∵P(3,4)为C上一点,∴-=1,
解得m=1,则B(1,0),∴kPB==2,
PB的中点坐标为(2,2),
PB的中垂线方程为y=-(x-2)+2,
令x=0,则y=3,
设外接圆圆心为M(0,t),
则M(0,3),r=|MB|==,
∴△PAB外接圆的标准方程为x2+(y-3)2=10.]
3.[由圆的一般方程求参数(或范围)](2021·珠海一模)若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则k的取值范围为________.
(-∞,1)∪(4,+∞) [根据题意,若方程
x2+y2+λxy+2kx+4y+5k+λ=0表示圆,
则λ=0,方程为x2+y2+2kx+4y+5k=0,
即(x+k)2+(y+2)2=k2-5k+4,
必有k2-5k+4>0,解得k<1或k>4,
即k的取值范围为(-∞,1)∪(4,+∞).]
考点3 直线与圆的位置关系
1.(2021·新高考卷Ⅰ改编)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则下列结论成立的是( )
①点P到直线AB的距离小于10;
②点P到直线AB的距离大于2;
③当∠PBA最小时,|PB|=3;
④当∠PBA最大时,|PB|=3.
A.①② B.②③
C.②③④ D.①③④
D [设圆(x-5)2+(y-5)2=16的圆心为M(5,5),由题易知直线AB的方程为+=1,即x+2y-4=0,则圆心M到直线AB的距离d==>4,所以直线AB与圆M相离,所以点P到直线AB的距离的最大值为4+d=4+,4+<5+=10,故①正确.
易知点P到直线AB的距离的最小值为d-4=-4,-4<-4=1,故②不正确.
过点B作圆M的两条切线,切点分别为N,Q,如图所示,连接MB,MN,MQ,则当∠PBA最小时,点P与N重合,|PB|===3,当∠PBA最大时,点P与Q重合,|PB|=3,故③④都正确.综上,选D.
]
2.(2020·全国卷Ⅰ)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点.过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
D [法一:由⊙M:x2+y2-2x-2y-2=0 ①,
得⊙M:(x-1)2+(y-1)2=4,所以圆心M(1,1).如图,连接AM,BM,易知四边形PAMB的面积为|PM|·|AB|,欲使|PM|·|AB|最小,只需四边形PAMB的面积最小,即只需△PAM的面积最小.因为|AM|=2,所以只需|PA|最小.又|PA|==,所以只需直线2x+y+2=0上的动点P到M的距离最小,其最小值为=,此时PM⊥l,易求出直线PM的方程为x-2y+1=0.由得所以P(-1,0).易知P,A,M,B四点共圆,所以以PM为直径的圆的方程为x2+=,即x2+y2-y-1=0 ②,由①②得,直线AB的方程为2x+y+1=0,故选D.
法二:因为⊙M:(x-1)2+(y-1)2=4,所以圆心M(1,1).
连接AM,BM,易知四边形PAMB的面积为|PM|·|AB|,欲使|PM|·|AB|最小,只需四边形PAMB的面积最小,即只需△PAM的面积最小.因为|AM|=2,所以只需|PA|最小.
又|PA|==,所以只需|PM|最小,此时PM⊥l.因为PM⊥AB,所以l∥AB,所以kAB=-2,排除A,C.
易求出直线PM的方程为x-2y+1=0,由得所以P(-1,0).因为点M到直线x=-1的距离为2,所以直线x=-1过点P且与⊙M相切,所以A(-1,1).因为点A(-1,1)在直线AB上,故排除B.故选D.]
3.(2020·天津高考)已知直线x-y+8=0和圆x2+y2=r2(r>0)相交于A,B两点.若|AB|=6,则r的值为________.
5 [依题意得,圆心(0,0)到直线x-y+8=0的距离d==4,因此r2=d2+=25,又r>0,所以r=5.]
命题规律:以直线与圆的位置关系为切入点,结合圆的几何性质,勾股定理及距离等相关知识考查数形结合及数学运算能力.一般以选择题、填空题的形式出现,知识相对综合,有一定的区分度.
通性通法:解决直线与圆的位置关系问题应关注3点
(1)处理直线与圆的位置关系问题时,主要利用几何法,即利用圆心到直线的距离与半径的大小关系判断,并依据相关几何性质求解.
(2)弦长问题,主要依据弦长的一半、弦心距、半径之间的关系求解.
(3)过圆内一点且垂直于过这点的半径的弦最短.
1.[直线与圆的关系](2021·广东二模)设直线l:y=kx+1(k∈R)与圆C:x2+y2=5,则下列结论正确的为( )
A.l与C可能相离
B.l可能将C的周长平分
C.当k=1时,l被C截得的弦长为
D.l被C截得的最短弦长为4
D [对于A选项,直线l过定点(0,1),且点(0,1)在圆C内,则直线l与圆C必相交,A选项错误;
对于B选项,若直线l将圆C平分,则直线l过原点,此时直线l的斜率不存在,B选项错误;
对于C选项,当k=1时,直线l的方程为x-y+1=0,圆心C到直线l的距离为d=,所以,直线l被C截得的弦长为2eq \r(5-\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(2),2))))=3,C选项错误;
对于D选项,圆心C到直线l的距离为d=≤1,
所以,直线l被C截得的弦长为2≥4,D选项正确.故选D.]
2.[圆与圆的位置关系]若圆x2+y2=4与圆x2+y2+ax+2ay-9=0(a>0)相交,公共弦的长为2,则a=________.
[联立两圆方程
可得公共弦所在直线方程为ax+2ay-5=0,
故圆心(0,0)到直线ax+2ay-5=0的距离为=(a>0).
故2eq \r(22-\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(5),a))))=2,解得a2=,
因为a>0,所以a=.]
3.[切线问题]设P为直线3x-4y+11=0上的动点,过点P作圆C:x2+y2-2x-2y+1=0的两条切线,切点分别为A,B,则四边形PACB的面积的最小值为________.
[圆的标准方程为(x-1)2+(y-1)2=1,圆心为C(1,1),半径为r=1,根据对称性可知,四边形PACB的面积为2S△APC=2×|PA|r=|PA|=,要使四边形PACB的面积最小,则只需|PC|最小,最小值为圆心到直线l:3x-4y+11=0的距离d===2.
所以四边形PACB面积的最小值为==.]
10/10
同课章节目录
