北师大版数学九年级下册 第2章 二次函数 单元测试(word版含解析)
文档属性
| 名称 | 北师大版数学九年级下册 第2章 二次函数 单元测试(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 131.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 08:32:36 | ||
图片预览



文档简介
第二章 二次函数 单元测试
一、选择题(每题4分,共28分)
1.下列函数中,是二次函数的是 ( )
A.y=
B.y=(x+3)2-x2
C.y=
D.y=x(x-1)
2.已知二次函数y=ax2+bx+c的如图象开口向下,顶点坐标为(2,-3),那么该函数有 ( )
A.最小值-3 B.最大值-3
C.最小值2 D.最大值2
3.若关于x的二次函数y=(m-1)x2-mx-m2+1的如图象过原点,则m的值为 ( )
A.±1 B.0
C.1 D.-1
4.如示,二次函数y=x2-4x+3的如图象与x轴交于A,B两点,与y轴交于点C,则△ABC的面积为 ( )
A.1 B.2
C.3 D.4
5.对于二次函数y=x2-2mx-3,下列结论错误的是 ( )
A.它的如图象与x轴有两个交点
B.关于x的方程x2-2mx=3的两根之积为-3
C.它的如图象的对称轴在y轴的右侧
D.当x6.如Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到Rt△OCD,边CD与该抛物线交于点P,则点P的坐标为 ( )
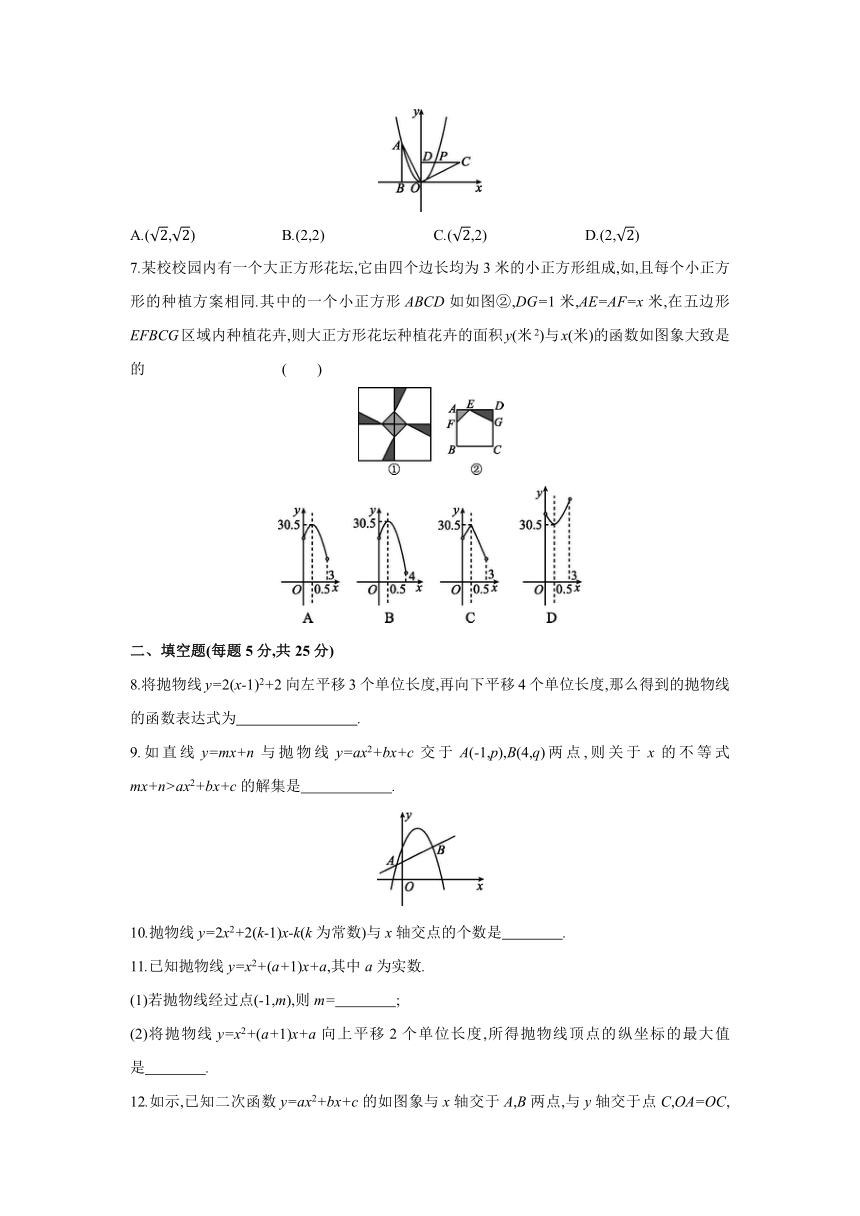
A.(,) B.(2,2) C.(,2) D.(2,)
7.某校校园内有一个大正方形花坛,它由四个边长均为3米的小正方形组成,如,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如如图②,DG=1米,AE=AF=x米,在五边形EFBCG区域内种植花卉,则大正方形花坛种植花卉的面积y(米2)与x(米)的函数如图象大致是的 ( )
二、填空题(每题5分,共25分)
8.将抛物线y=2(x-1)2+2向左平移3个单位长度,再向下平移4个单位长度,那么得到的抛物线的函数表达式为 .
9.如直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
10.抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是 .
11.已知抛物线y=x2+(a+1)x+a,其中a为实数.
(1)若抛物线经过点(-1,m),则m= ;
(2)将抛物线y=x2+(a+1)x+a向上平移2个单位长度,所得抛物线顶点的纵坐标的最大值是 .
12.如示,已知二次函数y=ax2+bx+c的如图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论:①abc<0;②a+b+c=0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的是 .(写出所有正确结论的序号)
三、解答题(共47分)
13.(14分)随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形水池,在水池中心竖直安装了一根高为2m的喷水管(如,它喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,水柱落地处离池中心3m.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数表达式;
(2)求出水柱的最大高度.
14.(15分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天的销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天的销售利润最大,最大利润是多少元
15.(18分)如抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y=-x-2经过点A,C.
(1)求抛物线的函数表达式;
(2)P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.当△PCM是直角三角形时,求点P的坐标.
答案
【作者说卷】
二次函数是初中阶段函数学习的最高形式,其如图象、性质、变化规律是其他函数所不能比拟的.本套试卷就二次函数的重点内容进行了考查,既有全面性,亦有侧重性.
知识点分布:(1)二次函数的表达式,如8,13,14,15题.
(2)二次函数的如图象,如5,6,10,12,13题.
(3)二次函数如图象的开口方向、对称轴、顶点坐标,如2,5题.
(4)二次函数的性质,如3,5题.
(5)二次函数和一元二次方程的关系,如4题.
(6)利用二次函数解决实际问题,如7,13,14题.
思想方法:表格、表达式、如图象三种表示方法的有机结合.
亮点:关注学生能否建立二次函数的如图象与表达式之间的联系,能否理解表达式的变化会引起如图象的变化,或者如图象的变化引起表达式的变化;关注学生能否把实际问题中的等量关系用二次函数表示,利用二次函数的知识解决实际问题.
1.D 2.B 3.D
4.C 解:当y=0时,0=x2-4x+3,
解得x1=1,x2=3,∴AB=2.
当x=0时,y=3,∴OC=3,∴△ABC的面积是AB·OC=×2×3=3.故选C.
5.C 6.C
7.A 解:S△AEF=AE·AF=x2,S△DEG=DG·DE=×1×(3-x)=,
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-x2-=-x2+x+,
则y=4×-x2+x+=-2x2+2x+30.
∵AE综上可得,y=-2x2+2x+30(0故选A.
8.y=2(x+2)2-2 9.x<-1或x>4
10.2 解:∵y=2x2+2(k-1)x-k(k为常数),
∴当y=0时,0=2x2+2(k-1)x-k,
∴b2-4ac=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴关于x的方程0=2x2+2(k-1)x-k有两个不相等的实数根,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
故答案为2.
11.(1)0 (2)2 解:(1)将点(-1,m)代入抛物线表达式y=x2+(a+1)x+a,
得(-1)2+(a+1)×(-1)+a=m,则m=0.
故答案为0.
(2)将抛物线y=x2+(a+1)x+a向上平移2个单位长度可得y=x2+(a+1)x+a+2,
∴y=x+2-(a-1)2+2,
∴抛物线顶点的纵坐标n=-(a-1)2+2.
∵-<0,∴n的最大值为2.故答案为2.
12.①④
13.解:(1)答案不唯一,如如图,以喷水管与地面的交点为原点,原点与水柱落地点所在直线为x轴,喷水管所在直线为y轴,建立平面直角坐标系.
由题意,设抛物线的函数表达式为y=a(x-1)2+k(0≤x≤3).
将点(3,0)和(0,2)的坐标代入,得
解得
∴抛物线的函数表达式为y=-(x-1)2+=-x2+x+2(0≤x≤3).
(2)∵抛物线的函数表达式为y=-(x-1)2+(0≤x≤3),
∴当x=1时,y最大值=,
∴水柱的最大高度是m.
14.解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
根据题意,得
解得
∴y与x之间的函数关系式为y=-5x+150.
(2)根据题意,得w=(x-10)(-5x+150)=-5(x-20)2+500.
∵-5<0,
∴当x<20时,w随着x的增大而增大.
∵10≤x≤15且x为整数,
∴当x=15时,w有最大值,
即w最大=-5×(15-20)2+500=375,
故当每瓶洗手液的售价定为15元时,超市销售该品牌洗手液每天的销售利润最大,最大利润为375元.
15.解:(1)∵直线y=-x-2交x轴于点A,交y轴于点C,
∴A(-4,0),C(0,-2).
∵抛物线y=ax2+x+c经过点A,C,
∴解得
∴抛物线的函数表达式为y=x2+x-2.
(2)∵点P的横坐标为m,
∴点P的坐标为m,m2+m-2.
当△PCM是直角三角形时,有以下两种情况:
①当∠CPM=90°时,PC∥x轴,点P的纵坐标为-2,
∴m2+m-2=-2,
解得m1=0(舍去),m2=-2.
∴点P的坐标为(-2,-2).
②当∠PCM=90°时,易得m>0,过点P作PN⊥y轴于点N,
∴∠CNP=∠AOC=90°.
∵∠NCP+∠ACO=90°,
∠OAC+∠ACO=90°,
∴∠NCP=∠OAC.∴△CNP∽△AOC,
∴=.
∵C(0,-2),N0,m2+m-2,
∴CN=m2+m,PN=m.
即=.
解得m3=0(舍去),m4=6.
∵当m=6时,×62+×6-2=10,
∴点P的坐标为(6,10).
综上所述,当△PCM是直角三角形时,点P的坐标为(-2,-2)或(6,10).
一、选择题(每题4分,共28分)
1.下列函数中,是二次函数的是 ( )
A.y=
B.y=(x+3)2-x2
C.y=
D.y=x(x-1)
2.已知二次函数y=ax2+bx+c的如图象开口向下,顶点坐标为(2,-3),那么该函数有 ( )
A.最小值-3 B.最大值-3
C.最小值2 D.最大值2
3.若关于x的二次函数y=(m-1)x2-mx-m2+1的如图象过原点,则m的值为 ( )
A.±1 B.0
C.1 D.-1
4.如示,二次函数y=x2-4x+3的如图象与x轴交于A,B两点,与y轴交于点C,则△ABC的面积为 ( )
A.1 B.2
C.3 D.4
5.对于二次函数y=x2-2mx-3,下列结论错误的是 ( )
A.它的如图象与x轴有两个交点
B.关于x的方程x2-2mx=3的两根之积为-3
C.它的如图象的对称轴在y轴的右侧
D.当x
A.(,) B.(2,2) C.(,2) D.(2,)
7.某校校园内有一个大正方形花坛,它由四个边长均为3米的小正方形组成,如,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如如图②,DG=1米,AE=AF=x米,在五边形EFBCG区域内种植花卉,则大正方形花坛种植花卉的面积y(米2)与x(米)的函数如图象大致是的 ( )
二、填空题(每题5分,共25分)
8.将抛物线y=2(x-1)2+2向左平移3个单位长度,再向下平移4个单位长度,那么得到的抛物线的函数表达式为 .
9.如直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
10.抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是 .
11.已知抛物线y=x2+(a+1)x+a,其中a为实数.
(1)若抛物线经过点(-1,m),则m= ;
(2)将抛物线y=x2+(a+1)x+a向上平移2个单位长度,所得抛物线顶点的纵坐标的最大值是 .
12.如示,已知二次函数y=ax2+bx+c的如图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论:①abc<0;②a+b+c=0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的是 .(写出所有正确结论的序号)
三、解答题(共47分)
13.(14分)随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形水池,在水池中心竖直安装了一根高为2m的喷水管(如,它喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,水柱落地处离池中心3m.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数表达式;
(2)求出水柱的最大高度.
14.(15分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天的销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天的销售利润最大,最大利润是多少元
15.(18分)如抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y=-x-2经过点A,C.
(1)求抛物线的函数表达式;
(2)P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.当△PCM是直角三角形时,求点P的坐标.
答案
【作者说卷】
二次函数是初中阶段函数学习的最高形式,其如图象、性质、变化规律是其他函数所不能比拟的.本套试卷就二次函数的重点内容进行了考查,既有全面性,亦有侧重性.
知识点分布:(1)二次函数的表达式,如8,13,14,15题.
(2)二次函数的如图象,如5,6,10,12,13题.
(3)二次函数如图象的开口方向、对称轴、顶点坐标,如2,5题.
(4)二次函数的性质,如3,5题.
(5)二次函数和一元二次方程的关系,如4题.
(6)利用二次函数解决实际问题,如7,13,14题.
思想方法:表格、表达式、如图象三种表示方法的有机结合.
亮点:关注学生能否建立二次函数的如图象与表达式之间的联系,能否理解表达式的变化会引起如图象的变化,或者如图象的变化引起表达式的变化;关注学生能否把实际问题中的等量关系用二次函数表示,利用二次函数的知识解决实际问题.
1.D 2.B 3.D
4.C 解:当y=0时,0=x2-4x+3,
解得x1=1,x2=3,∴AB=2.
当x=0时,y=3,∴OC=3,∴△ABC的面积是AB·OC=×2×3=3.故选C.
5.C 6.C
7.A 解:S△AEF=AE·AF=x2,S△DEG=DG·DE=×1×(3-x)=,
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-x2-=-x2+x+,
则y=4×-x2+x+=-2x2+2x+30.
∵AE
8.y=2(x+2)2-2 9.x<-1或x>4
10.2 解:∵y=2x2+2(k-1)x-k(k为常数),
∴当y=0时,0=2x2+2(k-1)x-k,
∴b2-4ac=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴关于x的方程0=2x2+2(k-1)x-k有两个不相等的实数根,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
故答案为2.
11.(1)0 (2)2 解:(1)将点(-1,m)代入抛物线表达式y=x2+(a+1)x+a,
得(-1)2+(a+1)×(-1)+a=m,则m=0.
故答案为0.
(2)将抛物线y=x2+(a+1)x+a向上平移2个单位长度可得y=x2+(a+1)x+a+2,
∴y=x+2-(a-1)2+2,
∴抛物线顶点的纵坐标n=-(a-1)2+2.
∵-<0,∴n的最大值为2.故答案为2.
12.①④
13.解:(1)答案不唯一,如如图,以喷水管与地面的交点为原点,原点与水柱落地点所在直线为x轴,喷水管所在直线为y轴,建立平面直角坐标系.
由题意,设抛物线的函数表达式为y=a(x-1)2+k(0≤x≤3).
将点(3,0)和(0,2)的坐标代入,得
解得
∴抛物线的函数表达式为y=-(x-1)2+=-x2+x+2(0≤x≤3).
(2)∵抛物线的函数表达式为y=-(x-1)2+(0≤x≤3),
∴当x=1时,y最大值=,
∴水柱的最大高度是m.
14.解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
根据题意,得
解得
∴y与x之间的函数关系式为y=-5x+150.
(2)根据题意,得w=(x-10)(-5x+150)=-5(x-20)2+500.
∵-5<0,
∴当x<20时,w随着x的增大而增大.
∵10≤x≤15且x为整数,
∴当x=15时,w有最大值,
即w最大=-5×(15-20)2+500=375,
故当每瓶洗手液的售价定为15元时,超市销售该品牌洗手液每天的销售利润最大,最大利润为375元.
15.解:(1)∵直线y=-x-2交x轴于点A,交y轴于点C,
∴A(-4,0),C(0,-2).
∵抛物线y=ax2+x+c经过点A,C,
∴解得
∴抛物线的函数表达式为y=x2+x-2.
(2)∵点P的横坐标为m,
∴点P的坐标为m,m2+m-2.
当△PCM是直角三角形时,有以下两种情况:
①当∠CPM=90°时,PC∥x轴,点P的纵坐标为-2,
∴m2+m-2=-2,
解得m1=0(舍去),m2=-2.
∴点P的坐标为(-2,-2).
②当∠PCM=90°时,易得m>0,过点P作PN⊥y轴于点N,
∴∠CNP=∠AOC=90°.
∵∠NCP+∠ACO=90°,
∠OAC+∠ACO=90°,
∴∠NCP=∠OAC.∴△CNP∽△AOC,
∴=.
∵C(0,-2),N0,m2+m-2,
∴CN=m2+m,PN=m.
即=.
解得m3=0(舍去),m4=6.
∵当m=6时,×62+×6-2=10,
∴点P的坐标为(6,10).
综上所述,当△PCM是直角三角形时,点P的坐标为(-2,-2)或(6,10).
