北师大版数学九年级下册 第3章 圆 单元复习小结(word版含解析)
文档属性
| 名称 | 北师大版数学九年级下册 第3章 圆 单元复习小结(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 08:39:55 | ||
图片预览



文档简介
单元复习小结
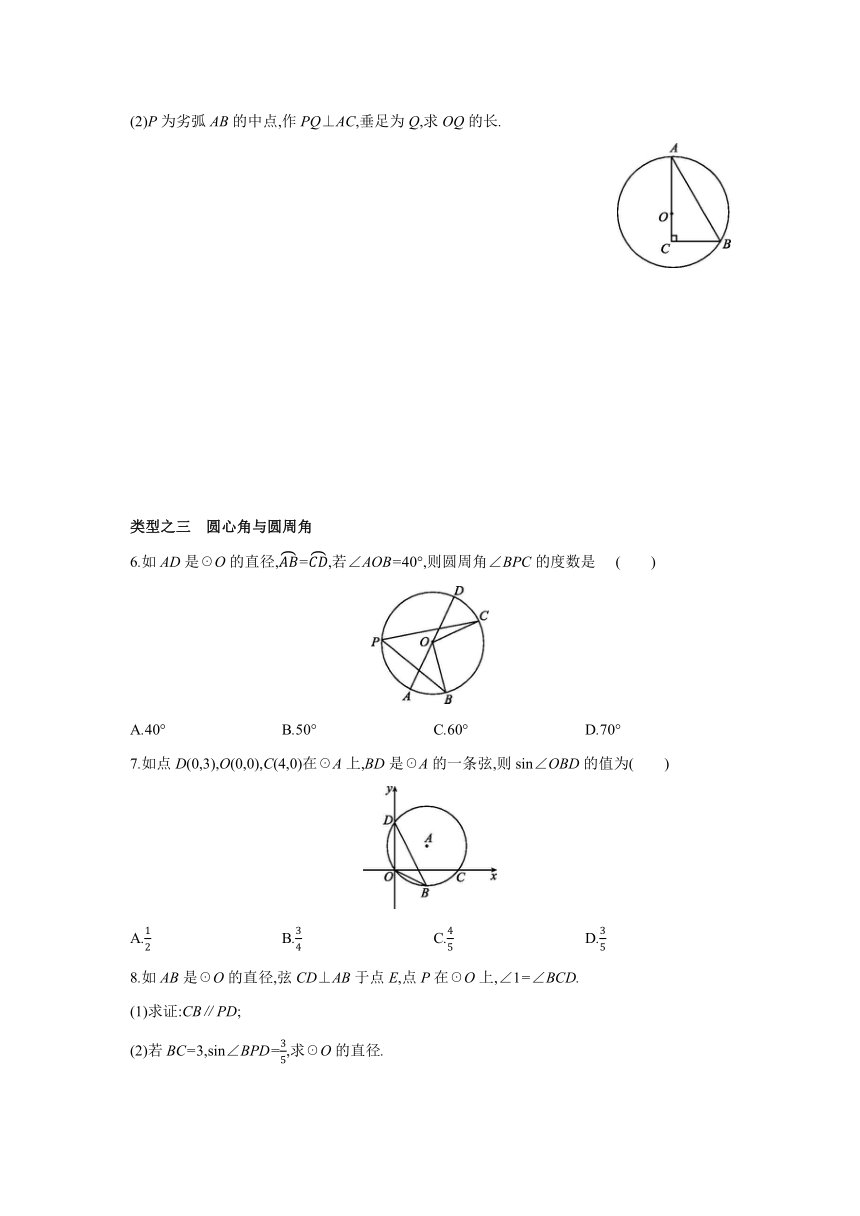
类型之一 圆的有关概念
1.下列命题中正确的有 ( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
2.如在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB长为半径的圆交AB于点D,连接CD,则∠ACD的度数为 ( )
A.10° B.15°
C.20° D.25°
类型之二 垂径定理及其推论的应用
3.如AB为☉O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD的长为 ( )
A.5 B.8 C.2 D.4
4.如一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
5.如在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的☉O经过点B.
(1)求☉O的半径;
(2)P为劣弧AB的中点,作PQ⊥AC,垂足为Q,求OQ的长.
类型之三 圆心角与圆周角
6.如AD是☉O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是 ( )
A.40° B.50° C.60° D.70°
7.如点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则sin∠OBD的值为( )
A. B. C. D.
8.如AB是☉O的直径,弦CD⊥AB于点E,点P在☉O上,∠1=∠BCD.
(1)求证:CB∥PD;
(2)若BC=3,sin∠BPD=,求☉O的直径.
类型之四 切线的判定与性质
9.如已知AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=40°,则∠B的度数是 .
10.如四边形ABCD内接于☉O,AB是直径,过点C的切线与AB的延长线交于点P,若∠P=40°,则∠D的度数为 .
11.如,△ABC内接于☉O,AB是☉O的直径,AC=CE,连接AE交BC于点D,延长DC至点F,使CF=CD,连接AF.
(1)判断直线AF与☉O的位置关系,并说明理由;
(2)若AC=10,tan∠CAE=,求AE的长.
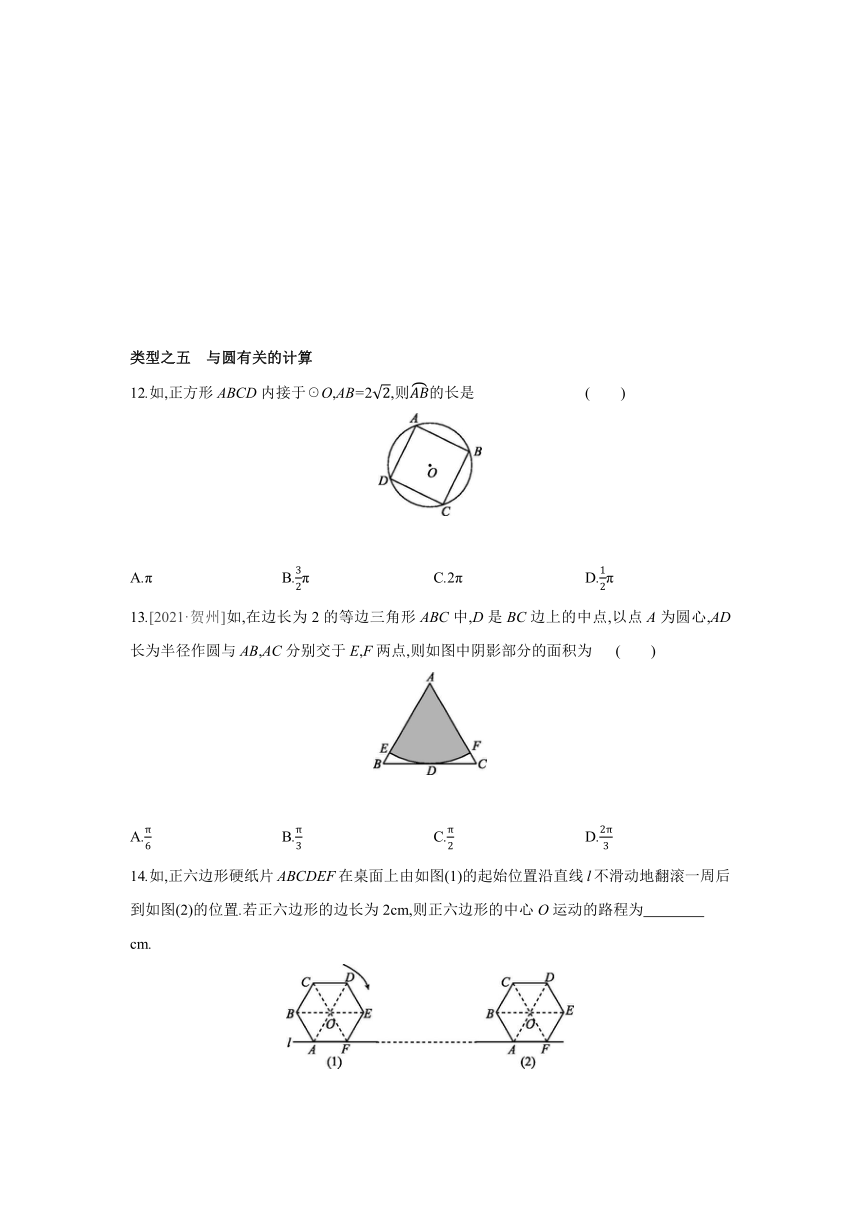
类型之五 与圆有关的计算
12.如,正方形ABCD内接于☉O,AB=2,则的长是 ( )
A.π B.π C.2π D.π
13.[2021·贺州]如,在边长为2的等边三角形ABC中,D是BC边上的中点,以点A为圆心,AD长为半径作圆与AB,AC分别交于E,F两点,则如图中阴影部分的面积为 ( )
A. B. C. D.
14.如,正六边形硬纸片ABCDEF在桌面上由如图(1)的起始位置沿直线l不滑动地翻滚一周后到如图(2)的位置.若正六边形的边长为2cm,则正六边形的中心O运动的路程为
cm.
15.(1)如①,已知△PAC是☉O的内接正三角形,那么∠OAC= °.
(2)如如图②,设AB是☉O的直径,AC是☉O的任意一条弦,∠OAC=α.
①如果α=45°,那么AC能否成为圆内接正多边形的一条边 若能,则此多边形是几边形
②若AC是☉O的内接正n边形的一边,则用含n的代数式表示α应为 ﹒
类型之六 圆的综合应用
16.如,AB为☉O的直径,CD为弦,且CD⊥AB,垂足为H,连接AC,OC.
(1)若∠BAC=30°,求证:CD平分OB;
(2)若E为的中点,连接OE,CE,求证:CE平分∠OCD;
(3)若☉O的半径为4,∠BAC=30°,则圆周上到直线AC的距离为3的点有多少个 请说明理由.
答案
1.A
2.A 解:∵∠ACB=90°,∠A=40°,
∴∠B=50°.
∵CD=CB,∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
故选A.
3.B 解:如如图,连接OD.
∵AB为☉O的直径,弦CD⊥AB于点E,
∴CD=2DE.
∵AE=8,BE=2,
∴☉O的半径为5,
∴OE=5-2=3.
在Rt△ODE中,∵OE=3,OD=5,
∴DE==4,
∴CD=2DE=8.
故选B.
4.10或70
5.解:(1)如如图①,过点O作OH⊥AB于点H.
在Rt△ACB中,∵∠C=90°,∠A=30°,BC=1,
∴AB=2BC=2.
∵OH⊥AB,∴AH=HB=1,
∴OA=AH÷cos30°=,
即☉O的半径为.
(2)如如图②,连接OP,PA.设OP交AB于点M.
∵=,∴OP⊥AB,∴∠AMO=90°.
∵∠OAM=30°,∴∠AOP=60°.
∵OA=OP,∴△AOP是等边三角形.
∵PQ⊥OA,∴OQ=QA=OA=.
6.B 7.D
8.解:(1)证明:∵∠D=∠1,∠1=∠BCD,
∴∠D=∠BCD,∴CB∥PD.
(2)如如图,连接AC.
∵AB是☉O的直径,
∴∠ACB=90°.
∵CD⊥AB,∴=,
∴∠BPD=∠CAB,
∴sin∠CAB=sin∠BPD=,即=.
∵BC=3,∴AB=5,即☉O的直径是5.
9.25° 解:∵AC是☉O的切线,
∴∠OAC=90°.
∵∠C=40°,∴∠AOD=50°,
∴∠B=∠AOD=25°.
故答案为25°.
10.115° 解:如如图,连接OC.
∵过点C的切线与AB的延长线交于点P,
∴∠OCP=90°,
∴∠COB=90°-∠P=50°.
∵OC=OB,∠COB=50°,
∴∠OCB=∠OBC=65°.
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=180°-65°=115°.
11.解:(1)直线AF与☉O相切.理由:
∵AB为☉O的直径,
∴∠ACB=90°,即AC⊥BC.
∵CF=CD,∴AD=AF,∴∠CAF=∠EAC.
∵AC=CE,∴∠E=∠EAC.
∵∠B=∠E,∴∠B=∠CAF.
∵∠B+∠BAC=90°,
∴∠CAF+∠BAC=90°,
∴∠BAF=90°,即OA⊥AF.
又∵点A在☉O上,∴直线AF与☉O相切.
(2)如如图,过点C作CM⊥AE于点M.
∵tan∠CAE=,∴=.
∵AC=10,∴设CM=3x,则AM=4x.
在Rt△ACM中,根据勾股定理,得CM2+AM2=AC2,
∴(3x)2+(4x)2=100,
解得x=2(负值已舍去),∴AM=8.
∵AC=CE,∴AE=2AM=2×8=16.
12.A 解:如如图,连接OA,OB.
∵正方形ABCD内接于☉O,
∴AB=BC=DC=AD,
∴===,
∴∠AOB=×360°=90°.
在Rt△AOB中,由勾股定理得2AO2=(2)2,
解得AO=2(负值已舍去),
∴的长为=π.
13.C 14.4π
15.解:(1)30
(2)①如果α=45°,那么AC能成为圆内接正多边形的一条边.
∵α=45°,
∴圆内接正多边形的中心角为90°,
∴此多边形是正方形﹒
②90°-
16.解:(1)证明:如如图,连接BC.
∵AB为☉O的直径,∴∠ACB=90°.
∵∠BAC=30°,∴∠B=60°.
又∵OC=OB,∴△OBC为等边三角形.
∵CD⊥OB,∴CD平分OB.
(2)证明:∵E为的中点,
∴∠AOE=∠BOE=90°,∴OE⊥AB.
∵CD⊥AB,∴OE∥CD,
∴∠OEC=∠ECD.
∵OC=OE,∴∠OEC=∠OCE,
∴∠OCE=∠ECD,即CE平分∠OCD.
(3)圆周上到直线AC的距离为3的点有2个.
理由如下:过点O作OF⊥AC于点F,交☉O于点G,如如图.
∵OA=4,∠BAC=30°,
∴OF=OA=2,
∴GF=OG-OF=2,
即上的点到直线AC的最大距离为2,
∴在上不存在到直线AC的距离为3的点.
而上的点到直线AC的最大距离为4+2=6,
∴在上到直线AC的距离为3的点有2个.
综上所述,圆周上到直线AC的距离为3的点有2个.
类型之一 圆的有关概念
1.下列命题中正确的有 ( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
2.如在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB长为半径的圆交AB于点D,连接CD,则∠ACD的度数为 ( )
A.10° B.15°
C.20° D.25°
类型之二 垂径定理及其推论的应用
3.如AB为☉O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD的长为 ( )
A.5 B.8 C.2 D.4
4.如一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
5.如在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的☉O经过点B.
(1)求☉O的半径;
(2)P为劣弧AB的中点,作PQ⊥AC,垂足为Q,求OQ的长.
类型之三 圆心角与圆周角
6.如AD是☉O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是 ( )
A.40° B.50° C.60° D.70°
7.如点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则sin∠OBD的值为( )
A. B. C. D.
8.如AB是☉O的直径,弦CD⊥AB于点E,点P在☉O上,∠1=∠BCD.
(1)求证:CB∥PD;
(2)若BC=3,sin∠BPD=,求☉O的直径.
类型之四 切线的判定与性质
9.如已知AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=40°,则∠B的度数是 .
10.如四边形ABCD内接于☉O,AB是直径,过点C的切线与AB的延长线交于点P,若∠P=40°,则∠D的度数为 .
11.如,△ABC内接于☉O,AB是☉O的直径,AC=CE,连接AE交BC于点D,延长DC至点F,使CF=CD,连接AF.
(1)判断直线AF与☉O的位置关系,并说明理由;
(2)若AC=10,tan∠CAE=,求AE的长.
类型之五 与圆有关的计算
12.如,正方形ABCD内接于☉O,AB=2,则的长是 ( )
A.π B.π C.2π D.π
13.[2021·贺州]如,在边长为2的等边三角形ABC中,D是BC边上的中点,以点A为圆心,AD长为半径作圆与AB,AC分别交于E,F两点,则如图中阴影部分的面积为 ( )
A. B. C. D.
14.如,正六边形硬纸片ABCDEF在桌面上由如图(1)的起始位置沿直线l不滑动地翻滚一周后到如图(2)的位置.若正六边形的边长为2cm,则正六边形的中心O运动的路程为
cm.
15.(1)如①,已知△PAC是☉O的内接正三角形,那么∠OAC= °.
(2)如如图②,设AB是☉O的直径,AC是☉O的任意一条弦,∠OAC=α.
①如果α=45°,那么AC能否成为圆内接正多边形的一条边 若能,则此多边形是几边形
②若AC是☉O的内接正n边形的一边,则用含n的代数式表示α应为 ﹒
类型之六 圆的综合应用
16.如,AB为☉O的直径,CD为弦,且CD⊥AB,垂足为H,连接AC,OC.
(1)若∠BAC=30°,求证:CD平分OB;
(2)若E为的中点,连接OE,CE,求证:CE平分∠OCD;
(3)若☉O的半径为4,∠BAC=30°,则圆周上到直线AC的距离为3的点有多少个 请说明理由.
答案
1.A
2.A 解:∵∠ACB=90°,∠A=40°,
∴∠B=50°.
∵CD=CB,∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
故选A.
3.B 解:如如图,连接OD.
∵AB为☉O的直径,弦CD⊥AB于点E,
∴CD=2DE.
∵AE=8,BE=2,
∴☉O的半径为5,
∴OE=5-2=3.
在Rt△ODE中,∵OE=3,OD=5,
∴DE==4,
∴CD=2DE=8.
故选B.
4.10或70
5.解:(1)如如图①,过点O作OH⊥AB于点H.
在Rt△ACB中,∵∠C=90°,∠A=30°,BC=1,
∴AB=2BC=2.
∵OH⊥AB,∴AH=HB=1,
∴OA=AH÷cos30°=,
即☉O的半径为.
(2)如如图②,连接OP,PA.设OP交AB于点M.
∵=,∴OP⊥AB,∴∠AMO=90°.
∵∠OAM=30°,∴∠AOP=60°.
∵OA=OP,∴△AOP是等边三角形.
∵PQ⊥OA,∴OQ=QA=OA=.
6.B 7.D
8.解:(1)证明:∵∠D=∠1,∠1=∠BCD,
∴∠D=∠BCD,∴CB∥PD.
(2)如如图,连接AC.
∵AB是☉O的直径,
∴∠ACB=90°.
∵CD⊥AB,∴=,
∴∠BPD=∠CAB,
∴sin∠CAB=sin∠BPD=,即=.
∵BC=3,∴AB=5,即☉O的直径是5.
9.25° 解:∵AC是☉O的切线,
∴∠OAC=90°.
∵∠C=40°,∴∠AOD=50°,
∴∠B=∠AOD=25°.
故答案为25°.
10.115° 解:如如图,连接OC.
∵过点C的切线与AB的延长线交于点P,
∴∠OCP=90°,
∴∠COB=90°-∠P=50°.
∵OC=OB,∠COB=50°,
∴∠OCB=∠OBC=65°.
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=180°-65°=115°.
11.解:(1)直线AF与☉O相切.理由:
∵AB为☉O的直径,
∴∠ACB=90°,即AC⊥BC.
∵CF=CD,∴AD=AF,∴∠CAF=∠EAC.
∵AC=CE,∴∠E=∠EAC.
∵∠B=∠E,∴∠B=∠CAF.
∵∠B+∠BAC=90°,
∴∠CAF+∠BAC=90°,
∴∠BAF=90°,即OA⊥AF.
又∵点A在☉O上,∴直线AF与☉O相切.
(2)如如图,过点C作CM⊥AE于点M.
∵tan∠CAE=,∴=.
∵AC=10,∴设CM=3x,则AM=4x.
在Rt△ACM中,根据勾股定理,得CM2+AM2=AC2,
∴(3x)2+(4x)2=100,
解得x=2(负值已舍去),∴AM=8.
∵AC=CE,∴AE=2AM=2×8=16.
12.A 解:如如图,连接OA,OB.
∵正方形ABCD内接于☉O,
∴AB=BC=DC=AD,
∴===,
∴∠AOB=×360°=90°.
在Rt△AOB中,由勾股定理得2AO2=(2)2,
解得AO=2(负值已舍去),
∴的长为=π.
13.C 14.4π
15.解:(1)30
(2)①如果α=45°,那么AC能成为圆内接正多边形的一条边.
∵α=45°,
∴圆内接正多边形的中心角为90°,
∴此多边形是正方形﹒
②90°-
16.解:(1)证明:如如图,连接BC.
∵AB为☉O的直径,∴∠ACB=90°.
∵∠BAC=30°,∴∠B=60°.
又∵OC=OB,∴△OBC为等边三角形.
∵CD⊥OB,∴CD平分OB.
(2)证明:∵E为的中点,
∴∠AOE=∠BOE=90°,∴OE⊥AB.
∵CD⊥AB,∴OE∥CD,
∴∠OEC=∠ECD.
∵OC=OE,∴∠OEC=∠OCE,
∴∠OCE=∠ECD,即CE平分∠OCD.
(3)圆周上到直线AC的距离为3的点有2个.
理由如下:过点O作OF⊥AC于点F,交☉O于点G,如如图.
∵OA=4,∠BAC=30°,
∴OF=OA=2,
∴GF=OG-OF=2,
即上的点到直线AC的最大距离为2,
∴在上不存在到直线AC的距离为3的点.
而上的点到直线AC的最大距离为4+2=6,
∴在上到直线AC的距离为3的点有2个.
综上所述,圆周上到直线AC的距离为3的点有2个.
