北师大版数学九年级下册同步课时练习:第1章 直角三角形的边角关系 单元复习小结(word版含答案)
文档属性
| 名称 | 北师大版数学九年级下册同步课时练习:第1章 直角三角形的边角关系 单元复习小结(word版含答案) | 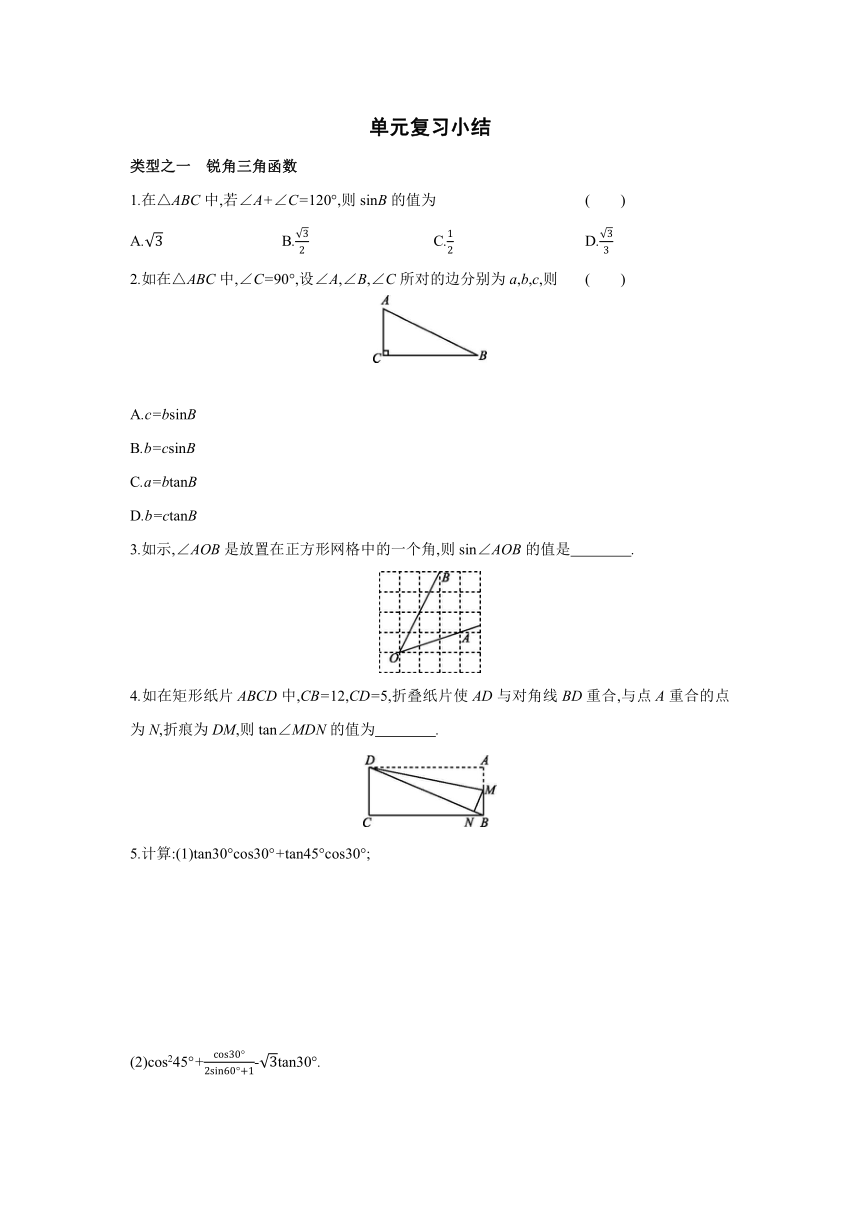 | |
| 格式 | docx | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-19 09:14:18 | ||
图片预览




文档简介
单元复习小结
类型之一 锐角三角函数
1.在△ABC中,若∠A+∠C=120°,则sinB的值为 ( )
A. B. C. D.
2.如在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则 ( )
A.c=bsinB
B.b=csinB
C.a=btanB
D.b=ctanB
3.如示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是 .
4.如在矩形纸片ABCD中,CB=12,CD=5,折叠纸片使AD与对角线BD重合,与点A重合的点为N,折痕为DM,则tan∠MDN的值为 .
5.计算:(1)tan30°cos30°+tan45°cos30°;
(2)cos245°+-tan30°.
类型之二 解直角三角形
6.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC= .
7.如在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
8.如∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求sin∠BAC的值和点B到直线MC的距离.
类型之三 三角函数的实际应用
9.为方便残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如线段BC表示“无障碍通道”,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)i=1∶2,BC=12米,CD=6米,∠D=30°,其中点A,B,C,D均在同一平面内,则垂直升降电梯AB的高度为( )
A.10米 B.(10-12)米
C.12米 D.(10+12)米
10.[2021·娄底]如我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得点A的仰角∠APD为30°,且点A与点P的距离为6km,它沿铅垂线上升7.5s后到达B处,此时在P处测得点B的仰角∠BPD为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,参考数据:≈1.732,≈1.414)
11.[2020·遂宁]在数学实践与综合课上,某兴趣小组的同学用航拍无人机对某居民小区的1,2号楼进行测高实践,如实践时绘制的截面如图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和点D,B为CD的中点,求2号楼的高度.(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°
≈0.92,cos67°≈0.39,tan67°≈2.36)
类型之四 综合与实践
12.阅读下列材料:
如,在△ABC中,∠BAC,∠B,∠C所对的边分别为a,b,c,可以得到S△ABC=absinC=acsinB=bcsin∠BAC.
证明:如如图①,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=,
∴AD=c·sinB,
∴S△ABC=a·AD=acsinB.
同理,S△ABC=absinC,S△ABC=bcsin∠BAC.
∴S△ABC=absinC=acsinB=bcsin∠BAC.
(1)根据上述材料,求证:==.
(2)运用(1)中的结论解决问题:
如如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长.
(3)如如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在点B测得点A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达点C,此时测得点A在北偏西45°方向上,根据以上信息,求A,B,C三点所围成的三角形的面积.
(本题参考数据:sin15°≈0.3,sin120°≈0.9,sin45°≈0.7,≈1.4,结果取整数)
答案
1.B 2.B
3. 解:如如图,连接AB.
设每个小正方形的边长都为1,则OA=AB=,OB=2,
∴OB2=OA2+AB2,∴∠OAB=90°,
∴△AOB是等腰直角三角形,
∴∠AOB=45°,∴sin∠AOB=.
故答案为.
4.
5.解:(1)原式=+1×=.
(2)原式=2+-
=+-1
=.
6.4+3或4-3
7.解:在Rt△ACD中,CD=6,tanA==,
∴AD=4,∴BD=AB-AD=8.
在Rt△BCD中,BC==10,
∴sinB==,cosB==,
∴sinB+cosB=.
8.解:如如图,过点B作BE⊥MC,垂足为E.
在Rt△ABC中,由勾股定理,得BC===5,
∴sin∠BAC==.
∵∠BCM=∠BAC,
∴在Rt△BEC中,BE=BC·sin∠BCE=BC·sin∠BAC=5×=,
即点B到直线MC的距离是.
9.B 解:如如图,延长AB交DC的延长线于点E,则AE⊥DE.
由BC的坡度(或坡比)i=1∶2,得BE∶CE=1∶2.
设BE=x米,则CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12(负值已舍去),
∴BE=12米,CE=24米,
∴DE=DC+CE=6+24=30(米).
由tan30°=,得=,
∴AE=10米,
∴AB=AE-BE=(10-12)米.
故选B.
10.解:由题意可得∠APD=30°,∠BPD=45°,AP=6km,∠BDP=90°.
在Rt△APD中,∵∠APD=30°,AP=6km,∴cos∠APD=cos30°=,AD=AP=3km,
∴PD=PA·cos30°=6×=3(km).
在Rt△BPD中,∵∠BPD=45°,PD=3km,∴tan∠BPD=tan45°=,
∴BD=PD·tan45°=3(km),
故AB=BD-AD=3-3≈2.196(km)=2196m,
则天舟二号从A处到B处的平均速度约为2196÷7.5≈293(m/s).
答:天舟二号从A处到B处的平均速度约为293m/s.
11.解:分别过点E,F作EM⊥AB,FN⊥AB,垂足分别为M,N,如如图.
由题意,得EC=20米,∠AEM=67°,∠AFN=40°,CB=DB=EM=FN,EC=MB,FD=NB,AB=60米,
∴AM=AB-MB=60-20=40(米).
在Rt△AEM中,
∵tan∠AEM=,
∴EM==≈16.95(米),
∴FN=EM≈16.95米.
在Rt△AFN中,
∵tan∠AFN=,
∴AN=FN·tan∠AFN≈tan40°×16.95≈14.24(米),
∴FD=NB=AB-AN≈60-14.24≈45.8(米).
故2号楼的高度约为45.8米.
12.解:(1)证明:∵absinC=acsinB,
∴bsinC=csinB,
∴=.
同理,=,
∴==.
(2)由(1)得=.
∵∠B=15°,∠C=60°,AB=20,
∴≈,
∴AC≈40×0.3=12,即AC的长约为12.
(3)由题意,得∠ABC=90°-75°=15°,∠ACB=90°-45°=45°,
∴∠A=180°-15°-45°=120°.
由==得=,∴AC≈6km,
∴S△ABC=AC·BC·sin∠ACB≈×6×18×0.7≈38(km2).
即A,B,C三点所围成的三角形的面积约为38km2.
类型之一 锐角三角函数
1.在△ABC中,若∠A+∠C=120°,则sinB的值为 ( )
A. B. C. D.
2.如在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则 ( )
A.c=bsinB
B.b=csinB
C.a=btanB
D.b=ctanB
3.如示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是 .
4.如在矩形纸片ABCD中,CB=12,CD=5,折叠纸片使AD与对角线BD重合,与点A重合的点为N,折痕为DM,则tan∠MDN的值为 .
5.计算:(1)tan30°cos30°+tan45°cos30°;
(2)cos245°+-tan30°.
类型之二 解直角三角形
6.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC= .
7.如在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
8.如∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求sin∠BAC的值和点B到直线MC的距离.
类型之三 三角函数的实际应用
9.为方便残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如线段BC表示“无障碍通道”,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)i=1∶2,BC=12米,CD=6米,∠D=30°,其中点A,B,C,D均在同一平面内,则垂直升降电梯AB的高度为( )
A.10米 B.(10-12)米
C.12米 D.(10+12)米
10.[2021·娄底]如我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得点A的仰角∠APD为30°,且点A与点P的距离为6km,它沿铅垂线上升7.5s后到达B处,此时在P处测得点B的仰角∠BPD为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,参考数据:≈1.732,≈1.414)
11.[2020·遂宁]在数学实践与综合课上,某兴趣小组的同学用航拍无人机对某居民小区的1,2号楼进行测高实践,如实践时绘制的截面如图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和点D,B为CD的中点,求2号楼的高度.(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°
≈0.92,cos67°≈0.39,tan67°≈2.36)
类型之四 综合与实践
12.阅读下列材料:
如,在△ABC中,∠BAC,∠B,∠C所对的边分别为a,b,c,可以得到S△ABC=absinC=acsinB=bcsin∠BAC.
证明:如如图①,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=,
∴AD=c·sinB,
∴S△ABC=a·AD=acsinB.
同理,S△ABC=absinC,S△ABC=bcsin∠BAC.
∴S△ABC=absinC=acsinB=bcsin∠BAC.
(1)根据上述材料,求证:==.
(2)运用(1)中的结论解决问题:
如如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长.
(3)如如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在点B测得点A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达点C,此时测得点A在北偏西45°方向上,根据以上信息,求A,B,C三点所围成的三角形的面积.
(本题参考数据:sin15°≈0.3,sin120°≈0.9,sin45°≈0.7,≈1.4,结果取整数)
答案
1.B 2.B
3. 解:如如图,连接AB.
设每个小正方形的边长都为1,则OA=AB=,OB=2,
∴OB2=OA2+AB2,∴∠OAB=90°,
∴△AOB是等腰直角三角形,
∴∠AOB=45°,∴sin∠AOB=.
故答案为.
4.
5.解:(1)原式=+1×=.
(2)原式=2+-
=+-1
=.
6.4+3或4-3
7.解:在Rt△ACD中,CD=6,tanA==,
∴AD=4,∴BD=AB-AD=8.
在Rt△BCD中,BC==10,
∴sinB==,cosB==,
∴sinB+cosB=.
8.解:如如图,过点B作BE⊥MC,垂足为E.
在Rt△ABC中,由勾股定理,得BC===5,
∴sin∠BAC==.
∵∠BCM=∠BAC,
∴在Rt△BEC中,BE=BC·sin∠BCE=BC·sin∠BAC=5×=,
即点B到直线MC的距离是.
9.B 解:如如图,延长AB交DC的延长线于点E,则AE⊥DE.
由BC的坡度(或坡比)i=1∶2,得BE∶CE=1∶2.
设BE=x米,则CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12(负值已舍去),
∴BE=12米,CE=24米,
∴DE=DC+CE=6+24=30(米).
由tan30°=,得=,
∴AE=10米,
∴AB=AE-BE=(10-12)米.
故选B.
10.解:由题意可得∠APD=30°,∠BPD=45°,AP=6km,∠BDP=90°.
在Rt△APD中,∵∠APD=30°,AP=6km,∴cos∠APD=cos30°=,AD=AP=3km,
∴PD=PA·cos30°=6×=3(km).
在Rt△BPD中,∵∠BPD=45°,PD=3km,∴tan∠BPD=tan45°=,
∴BD=PD·tan45°=3(km),
故AB=BD-AD=3-3≈2.196(km)=2196m,
则天舟二号从A处到B处的平均速度约为2196÷7.5≈293(m/s).
答:天舟二号从A处到B处的平均速度约为293m/s.
11.解:分别过点E,F作EM⊥AB,FN⊥AB,垂足分别为M,N,如如图.
由题意,得EC=20米,∠AEM=67°,∠AFN=40°,CB=DB=EM=FN,EC=MB,FD=NB,AB=60米,
∴AM=AB-MB=60-20=40(米).
在Rt△AEM中,
∵tan∠AEM=,
∴EM==≈16.95(米),
∴FN=EM≈16.95米.
在Rt△AFN中,
∵tan∠AFN=,
∴AN=FN·tan∠AFN≈tan40°×16.95≈14.24(米),
∴FD=NB=AB-AN≈60-14.24≈45.8(米).
故2号楼的高度约为45.8米.
12.解:(1)证明:∵absinC=acsinB,
∴bsinC=csinB,
∴=.
同理,=,
∴==.
(2)由(1)得=.
∵∠B=15°,∠C=60°,AB=20,
∴≈,
∴AC≈40×0.3=12,即AC的长约为12.
(3)由题意,得∠ABC=90°-75°=15°,∠ACB=90°-45°=45°,
∴∠A=180°-15°-45°=120°.
由==得=,∴AC≈6km,
∴S△ABC=AC·BC·sin∠ACB≈×6×18×0.7≈38(km2).
即A,B,C三点所围成的三角形的面积约为38km2.
