【满分计划】第二章 二次函数精选精练卷(含解析)
文档属性
| 名称 | 【满分计划】第二章 二次函数精选精练卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 844.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 21:08:18 | ||
图片预览


文档简介
第二章 二次函数
一、单选题(共20分)
1.关于函数,下列说法:①函数的最小值为1;②函数图象的对称轴为直线x=3;③当x≥0时,y随x的增大而增大;④当x≤0时,y随x的增大而减小,其中正确的有( )个.
A.1 B.2 C.3 D.4
2.二次函数的图象如图所示,对称轴是直线.下列结论:①;②;③;④(为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.由二次函数,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大
4.三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
5.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
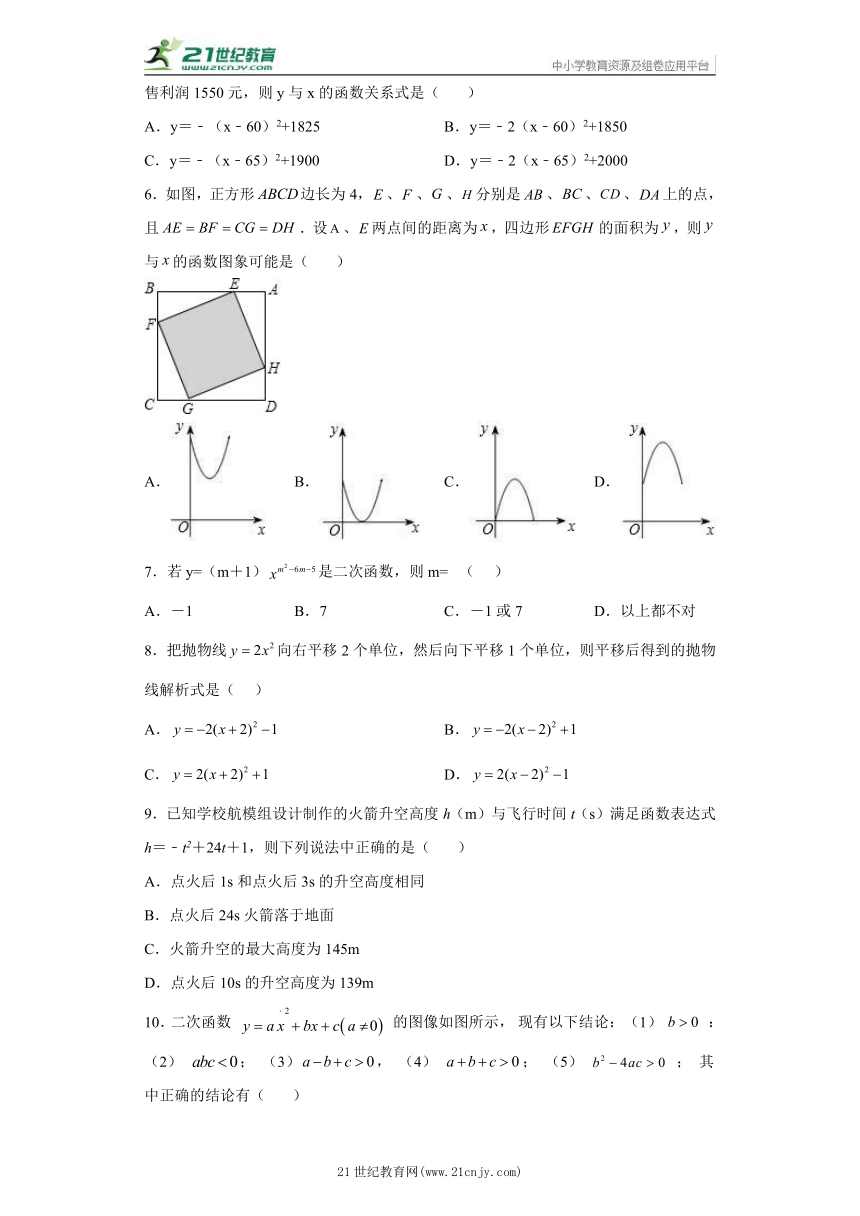
6.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是( )
A. B. C. D.
7.若y=(m+1)是二次函数,则m= ( )
A.-1 B.7 C.-1或7 D.以上都不对
8.把抛物线向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )
A. B.
C. D.
9.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
10.二次函数 的图像如图所示, 现有以下结论: (1) : (2) ; (3), (4) ; (5) ; 其中正确的结论有( )
A.2 个 B.3 个 C.4 个 D.5 个.
二、填空题(共40分)
11.将二次函数化成一般形式,其中二次项系数为________,一次项系数为________,常数项为________.
12.已知二次函数,当分别取时,函数值相等,则当取时,函数值为______.
13.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是_____.
14.已知关于的一元二次方程,有下列结论:
①当时,方程有两个不相等的实根;
②当时,方程不可能有两个异号的实根;
③当时,方程的两个实根不可能都小于1;
④当时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为_________.
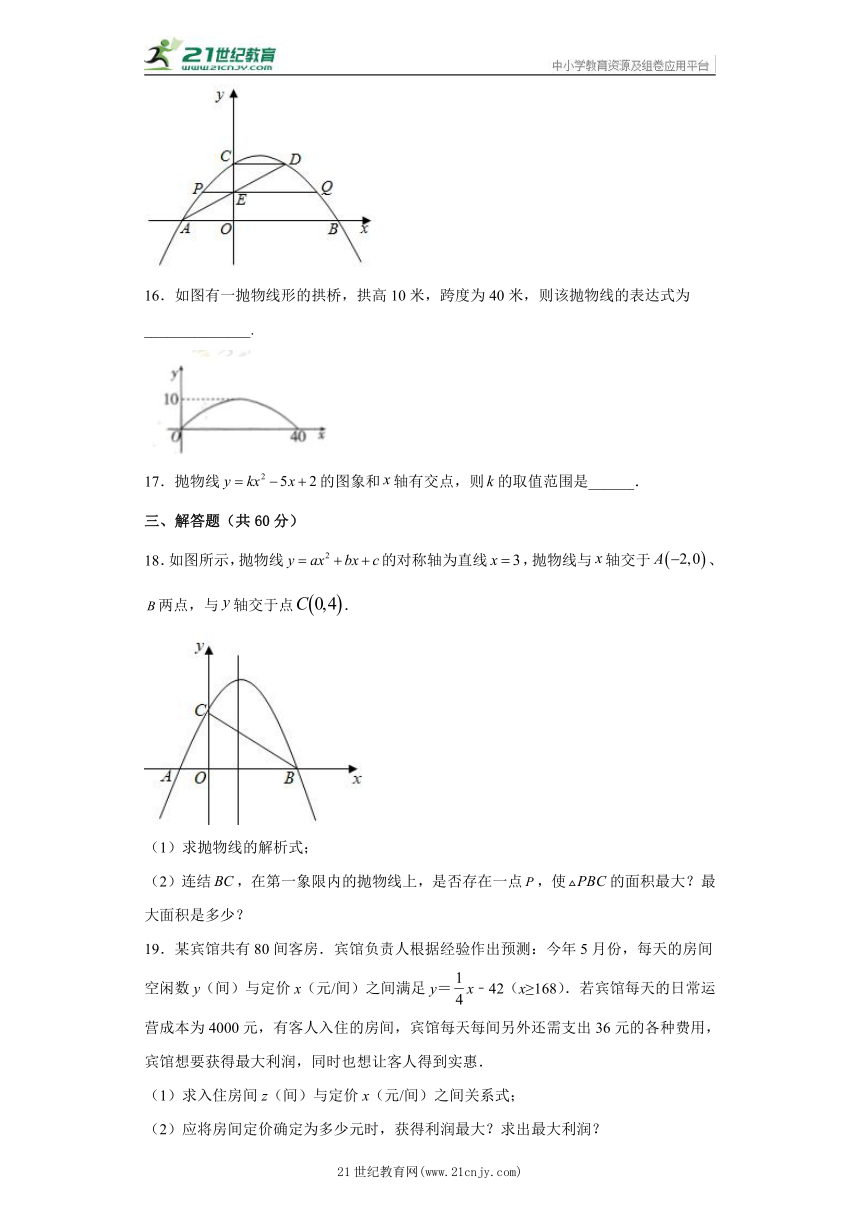
15.如图,抛物线y=﹣x2+x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
16.如图有一抛物线形的拱桥,拱高10米,跨度为40米,则该抛物线的表达式为______________.
17.抛物线的图象和轴有交点,则的取值范围是______.
三、解答题(共60分)
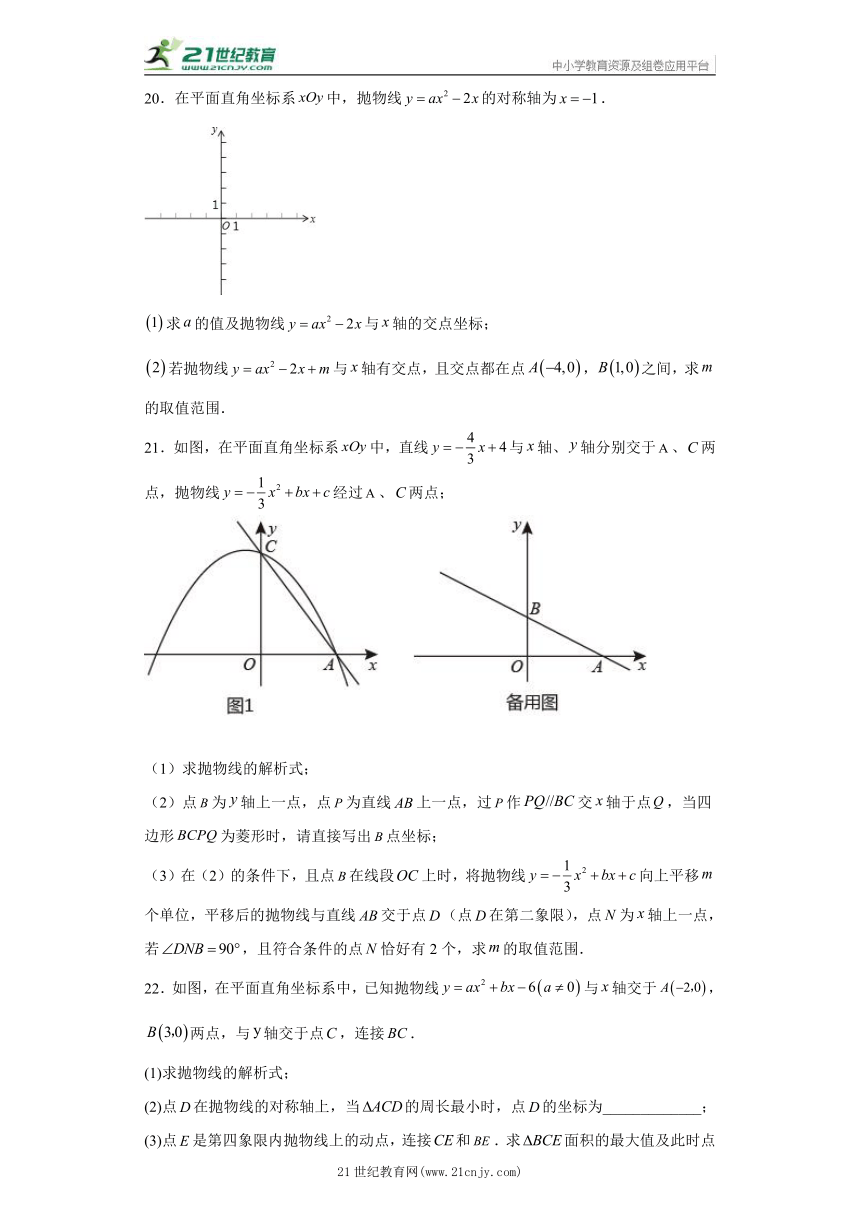
18.如图所示,抛物线的对称轴为直线,抛物线与轴交于、两点,与轴交于点.
(1)求抛物线的解析式;
(2)连结,在第一象限内的抛物线上,是否存在一点,使的面积最大?最大面积是多少?
19.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年5月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为4000元,有客人入住的房间,宾馆每天每间另外还需支出36元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠.
(1)求入住房间z(间)与定价x(元/间)之间关系式;
(2)应将房间定价确定为多少元时,获得利润最大?求出最大利润?
20.在平面直角坐标系中,抛物线的对称轴为.
求的值及抛物线与轴的交点坐标;
若抛物线与轴有交点,且交点都在点,之间,求的取值范围.
21.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,抛物线经过、两点;
(1)求抛物线的解析式;
(2)点为轴上一点,点为直线上一点,过作交轴于点,当四边形为菱形时,请直接写出点坐标;
(3)在(2)的条件下,且点在线段上时,将抛物线向上平移个单位,平移后的抛物线与直线交于点(点在第二象限),点为轴上一点,若,且符合条件的点恰好有2个,求的取值范围.
22.如图,在平面直角坐标系中,已知抛物线与轴交于,两点,与轴交于点,连接.
(1)求抛物线的解析式;
(2)点在抛物线的对称轴上,当的周长最小时,点的坐标为_____________;
(3)点是第四象限内抛物线上的动点,连接和.求面积的最大值及此时点的坐标;
(4)若点是对称轴上的动点,在抛物线上是否存在点,使以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
23.如图是两条互相垂直的街道, 且A到B, C的距离都是4千米. 现甲从B地走向A地, 乙从A地走向C地, 若两人同时出发且速度都是4千米/时, 问何时两人之间的距离最近
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【解析】
【分析】
根据所给函数的顶点式得出函数图象的性质从而判断选项的正确性.
【详解】
解:∵,
∴该函数图象开口向上,有最小值1,故①正确;
函数图象的对称轴为直线,故②错误;
当x≥0时,y随x的增大而增大,故③正确;
当x≤﹣3时,y随x的增大而减小,当﹣3≤x≤0时,y随x的增大而增大,故④错误.
故选:B.
【点睛】
本题考查二次函数的性质,解题的关键是能够根据函数解析式分析出函数图象的性质.
2.C
【解析】
【分析】
①由抛物线开口方向得到,对称轴在轴右侧,得到与异号,又抛物线与轴正半轴相交,得到,可得出,选项①错误;
②把代入中得,所以②正确;
③由时对应的函数值,可得出,得到,由,,,得到,选项③正确;
④由对称轴为直线,即时,有最小值,可得结论,即可得到④正确.
【详解】
解:①∵抛物线开口向上,∴,
∵抛物线的对称轴在轴右侧,∴,
∵抛物线与轴交于负半轴,
∴,
∴,①错误;
②当时,,∴,
∵,∴,
把代入中得,所以②正确;
③当时,,∴,
∴,
∵,,,
∴,即,所以③正确;
④∵抛物线的对称轴为直线,
∴时,函数的最小值为,
∴,
即,所以④正确.
故选C.
【点睛】
本题考查了二次函数图象与系数的关系:二次项系数决定抛物线的开口方向和大小.当时,抛物线向上开口;当时,抛物线向下开口;一次项系数和二次项系数共同决定对称轴的位置:当与同号时,对称轴在轴左;当与异号时,对称轴在轴右.常数项决定抛物线与轴交点:抛物线与轴交于.抛物线与轴交点个数由判别式确定:时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.
3.C
【解析】
【分析】
根据二次函数的性质,直接根据的值得出开口方向,再利用顶点坐标的对称轴和增减性,分别分析即可.
【详解】
解:由二次函数,可知:
.,其图象的开口向上,故此选项错误;
.其图象的对称轴为直线,故此选项错误;
.其最小值为1,故此选项正确;
.当时,随的增大而减小,故此选项错误.
故选:.
【点睛】
此题主要考查了二次函数的性质,同学们应根据题意熟练地应用二次函数性质,这是中考中考查重点知识.
4.B
【解析】
【分析】
根据题意,可以画出相应的抛物线,然后即可得到大孔所在抛物线解析式,再求出顶点为A的小孔所在抛物线的解析式,将x=﹣10代入可求解.
【详解】
解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=-,
∴大孔所在抛物线解析式为y=-x2+,设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为-7,
∴点E坐标为(-7,-),
∴-=m(x﹣b)2,
∴x1=+b,x2=-+b,
∴MN=4,
∴|+b-(-+b)|=4
∴m=-,
∴顶点为A的小孔所在抛物线的解析式为y=-(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=-10时,y=-,
∴-=-(x﹣b)2,
∴x1=+b,x2=-+b,
∴单个小孔的水面宽度=|(+b)-(-+b)|=5(米),
故选:B.
【点睛】
本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.
5.D
【解析】
【分析】
设二次函数的解析式为:y=ax2+bx+c,根据题意列方程组即可得到结论.
【详解】
解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,y=1800,当x=75,y=1800,当x=80时,y=1550,
∴,
解得a= 2,b=260,c= 6450,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
【点睛】
本题考查了根据实际问题列二次函数关系式,正确的列方程组是解题的关键.
6.A
【解析】
【分析】
本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y的表达式,结合选项的图象可得答案.
【详解】
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
【点睛】
本题考查了动点问题的函数图象,正确地写出函数解析式并数形结合分析是解题的关键.
7.B
【解析】
【分析】
令x的指数为2,系数不为0,列出方程与不等式解答即可.
【详解】
由题意得:m2-6m-5=2;且m+1≠0;
解得m=7或-1;m≠-1,
∴m=7,
故选:B.
【点睛】
利用二次函数的定义,二次函数中自变量的指数是2;二次项的系数不为0.
8.D
【解析】
【分析】
直接根据“左加右减,上加下减”的原则进行解答即可.
【详解】
由“左加右减”的原则可知,抛物线y=2x2向右平移2个单位所得抛物线是y=2(x 2)2;
由“上加下减”的原则可知,抛物线y=2(x 2)2向下平移1个单位所得抛物线是y=2(x 2)2 1.
故选D.
【点睛】
本题考查了二次函数图象与几何变换,解题的关键是掌握二次函数图象与几何变换.
9.C
【解析】
【分析】
分别求出t=1、3、24、10时h的值可判断A、B、D三个选项,将解析式配方成顶点式可判断C选项.
【详解】
解:A、当t=1时,h=24;当t=3时,h=64;所以点火后1s和点火后3s的升空高度不相同,此选项错误;
B、当t=24时,h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、由h=﹣t2+24t+1=﹣(t-12)2+145知火箭升空的最大高度为145m,此选项正确;
D、当t=10时,h=141m,此选项错误;
故选:C.
【点睛】
本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
10.C
【解析】
【分析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【详解】
解:(1)∵函数开口向下,∴a<0,∵对称轴在y轴的右边,∴,∴b>0,故命题正确;
(2)∵a<0,b>0,c>0,∴abc<0,故命题正确;
(3)∵当x=-1时,y<0,∴a-b+c<0,故命题错误;
(4)∵当x=1时,y>0,∴a+b+c>0,故命题正确;
(5)∵抛物线与x轴于两个交点,∴b2-4ac>0,故命题正确;
故选C.
【点睛】
本题考查了二次函数图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.
11.
【解析】
【分析】
通过去括号,移项,可以把方程化成二次函数的一般形式,然后确定二次项系数,一次项系数,常数项.
【详解】
y=﹣2(x﹣2)2变形为:y=﹣2x2+8x﹣8,所以二次项系数为﹣2;一次项系数为8;常数项为﹣8.
故答案为﹣2,8,﹣8.
【点睛】
本题考查的是二次函数的一般形式,通过去括号,移项,合并同类项,得到二次函数的一般形式,确定二次项系数,一次项系数,常数项的值.
12.2020
【解析】
【分析】
根据二次函数y=2x2+2020,当x分别取x1,x2(x1≠x2)时,函数值相等,可以得到x1和x2的关系,从而可以得到2x1+2x2的值,进而可以求得当x取2x1+2x2时,函数的值.
【详解】
解:∵二次函数y=2x2+2020,当x分别取x1,x2(x1≠x2)时,函数值相等,
∴2x12+2020=2x22+2020,
∴x1=-x2,
∴2x1+2x2=2(x1+x2)=0,
∴当x=2x1+2x2时,y=2×0+2020=0+2020=2020,
故答案为:2020.
【点睛】
本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
13.﹣3<x<1
【解析】
【分析】
根据抛物线与x轴的一个交点坐标和对称轴,由抛物线的对称性可求抛物线与x轴的另一个交点,再根据抛物线的增减性可求当y<0时,x的取值范围.
【详解】
解:∵抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为(﹣3,0),对称轴为x=﹣1,
∴抛物线与x轴的另一个交点为(1,0),
由图象可知,当y<0时,x的取值范围是﹣3<x<1.
故答案为:﹣3<x<1.
【点睛】
本题考查了二次函数的性质和数形结合能力,熟练掌握并灵活运用是解题的关键.
14.①③④
【解析】
【分析】
由根的判别式,根与系数的关系进行判断,即可得到答案.
【详解】
解:根据题意,∵一元二次方程,
∴;
∴当,即时,方程有两个不相等的实根;故①正确;
当,解得:,方程有两个同号的实数根,则当时,方程可能有两个异号的实根;故②错误;
抛物线的对称轴为:,则当时,方程的两个实根不可能都小于1;故③正确;
由,则,解得:或;故④正确;
∴正确的结论有①③④;
故答案为:①③④.
【点睛】
本题考查了二次函数的性质,一元二次方程根的判别式,根与系数的关系,解题的关键是掌握所学的知识进行解题.
15.2
【解析】
【分析】
利用二次函数图象上点的坐标特征可求出点A,B,C,D的坐标,由点A,D的坐标,利用待定系数法可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点E的坐标,再利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可求出线段PQ的长.
【详解】
解:当y=0时,﹣x2+x+2=0,
解得:x1=﹣2,x2=4,
∴点A的坐标为(﹣2,0);
当x=0时,y=﹣x2+x+2=2,
∴点C的坐标为(0,2);
当y=2时,﹣x2+x+2=2,
解得:x1=0,x2=2,
∴点D的坐标为(2,2).
设直线AD的解析式为y=kx+b(k≠0),
将A(﹣2,0),D(2,2)代入y=kx+b,得:
解得:
∴直线AD的解析式为y=x+1.
当x=0时,y=x+1=1,
∴点E的坐标为(0,1).
当y=1时,﹣x2+x+2=1,
解得:x1=1﹣,x2=1+,
∴点P的坐标为(1﹣,1),点Q的坐标为(1+,1),
∴PQ=1+﹣(1﹣)=2.
故答案为:2.
【点睛】
本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,利用二次函数图象上点的坐标特征求出点P,Q的坐标是解题的关键.
16.
【解析】
【分析】
由题意抛物线过点(40,0),顶点坐标为(20,10),设抛物线的解析式为,从而求出a的值,然后确定抛物线的解析式.
【详解】
解:依题意得此函数解析式顶点为,
∴设解析式为,
又函数图象经过,
,
,
.
故答案为 .
【点睛】
本题主要考查用待定系数法确定二次函数的解析式,解题时应根据情况设抛物线的解析式从而使解题简单,此题设为顶点式比较简单.
17.且
【解析】
【分析】
由题意知,,计算求解即可.
【详解】
解:由题意知,
解得
故答案为:且.
【点睛】
本题考查了二次函数与轴的交点个数.解题的关键在于熟练掌握二次函数与轴的交点个数.
18.(1);(2)存在,当时,面积最大为16,此时点点坐标为.
【解析】
【分析】
(1)用待定系数法解答便可;
(2)设点的坐标为,连结、、.根据对称性求出点B的坐标,根据得到二次函数关系式,最后配方求解即可.
【详解】
解:(1)∵抛物线过点,
∴.
∵抛物线的对称轴为直线,
∴可设抛物线为.
∵抛物线过点,
∴,解得.
∴抛物线的解析式为,即.
(2)存在,设点的坐标为,连结、、.
∵点A、关于直线对称,且
∴.
∴
.
∵
∴当时,面积最大为16,此时点点坐标为.
【点睛】
本题主要考查了二次函数的图象与性质,待定系数法,三角形面积公式以及二次函数的最值求法,根据图形得出由此得出二次函数关系式是解答此题的关键.
19.(1)z=﹣x+122(x≥168);(2)应将房间定价确定为260元时,获得利润最大,最大利润为8767元
【解析】
【分析】
(1)入住房间z(间)等于80减去每天的房间空闲数,列式并化简即可;
(2)设利润为w元,由题意得w关于x的二次函数关系式,根据二次函数的对称性及问题实际可得答案.
【详解】
解:(1)由题意得:
z=80﹣(x﹣42)
=﹣x+122,
∴入住房间z(间)与定价x(元/间)之间关系式为z=﹣x+122(x≥168);
(2)设利润为w元,由题意得:
w=(﹣x+122)x﹣36(﹣x+122)﹣4000
=﹣x2+131x﹣8392,
当x=﹣=262时,w最大,此时z=56.5非整数,不合题意,
∴x=260或264时,w最大,
∵让客人得到实惠,
∴x=260,
∴w最大==﹣×2602+131×260﹣8392=8767,
∴应将房间定价确定为260元时,获得利润最大,最大利润为8767元.
【点睛】
本题考查了二次函数在实际问题中的应用,理清题中的数量关系、熟练掌握二次函数的性质是解题的关键.
20.(1) a=-1;坐标为,;(2).
【解析】
【分析】
(1)利用抛物线的对称轴方程得到x=-=-1,解方程求出a即可得到抛物线的解析式为y=-x2-2x;然后解方程-x2-2x=0可得到抛物线与x轴的交点坐标;
(2)抛物线y=-x2-2x+m由抛物线y=-x2-2x上下平移|m|和单位得到,利用函数图象可得到当x=1时,y<0,即-1-2+m<0;当x=-1时,y≥0,即-1+2+m≥0,然后解两个不等式求出它们的公共部分可得到m的范围.
【详解】
根据题意得,解得,
所以抛物线的解析式为,
当时,,解得,,
所以抛物线与轴的交点坐标为,;
抛物线抛物线由抛物线上下平移和单位得到,而抛物线的对称轴为直线,
∵抛物线与轴的交点都在点,之间,
∴当时,,即,解得;
当时,,即,解得,
∴的取值范围为.
【点睛】
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象的几何变换.
21.(1);(2);;(3)
【解析】
【分析】
(1)由题意易得,,然后代入抛物线解析式进行求解即可;
(2)由题意可画出图象,设点,然后求出直线AB的解析式为,则可设点,点,进而根据中点坐标公式及两点距离公式可进行求解;
(3)过作轴交于,由(2)可得:,,则有,设,,进而可得,则,然后可得,则有,最后根据一元二次方程根的判别式可进行求解.
【详解】
解:(1)∵直线与轴、轴分别交于、两点,
∴,,
∵抛物线经过、两点,
∴,解得:,
∴抛物线的解析式为;
(2)由(1)可得,,由题意可得如图所示:
设点,直线AB的解析式为,把点A、B代入得:
,解得:,
∴直线AB的解析式为,
设点,点,
∵四边形是菱形,
∴根据中点坐标公式可得:,即,
∴,
∵,
∴根据两点距离公式可得:,
解得:或或(不符合题意,舍去),
∴;;
(3)过作轴交于,如图所示:
由(2)可得:,,
∴,
设,,
∵,
∴,
∴,
,
∵,,
∴,
∴,
∴,
∴,即,
化简得:,
当方程有唯一实根时,满足条件的只有一个,
∴,
化简得:,
解得:,(含去)
∴,
设平移后的抛物线为:,将点坐标代入平移后解析式得:
,
解得:,
.
【点睛】
本题主要考查二次函数的综合及相似三角形的性质与判定,熟练掌握二次函数的综合及相似三角形的性质与判定是解题的关键.
22.(1);(2);(3)面积最大为,点坐标为;(4)存在点,使以点、、、为顶点的四边形是平行四边形,,点坐标为,,.
【解析】
【分析】
(1)将点,代入即可求解;
(2)BC与对称轴的交点即为符合条件的点,据此可解;
(3)过点作轴于点,交直线与点,当EF最大时面积的取得最大值,据此可解;
(4)根据平行四边形对边平行且相等的性质可以得到存在点N使得以B,C,M,N为顶点的四边形是平行四边形.分三种情况讨论.
【详解】
解:(1) 抛物线过点,
解得:
抛物线解析式为.
(2) 点,
∴抛物线对称轴为直线
点在直线上,点,关于直线对称
,
当点、、在同一直线上时,最小.
抛物线解析式为,
∴C(0,-6),
设直线解析式为
,
解得:
直线:
,
,
故答案为:.
(3)过点作轴于点,交直线与点,
设,则
,
当时,面积最大为
,
此时点坐标为.
(4)存在点,使以点、、、为顶点的四边形是平行四边形.
设N(x,y),M(,m),
①四边形CMNB是平行四边形时,CM∥NB,CB∥MN,
,
∴x= ,
∴y= = ,
∴N(,);
②四边形CNBM是平行四边形时,CN∥BM,CM∥BN,
,
∴x=,
∴y==
∴N(,);
③四边形CNMB是平行四边形时,CB∥MN,NC∥BM,
,
∴x=,
∴y==
∴N(,);
点坐标为(,),(,),(,).
【点睛】
本题考查二次函数与几何图形的综合题,熟练掌握二次函数的性质,灵活运用数形结合思想得到坐标之间的关系是解题的关键.
23.当t=(在0【解析】
【分析】
设两人均出发了t时,根据勾股定理建立甲、乙之间的距离与时间t的函数关系式,然后求出二次函数在一定的取值范围内的最值即可得解.
【详解】
设两人均出发了t时, 则此时甲到A地的距离是(4-4t)千米, 乙离A地的距离是4t千米, 由勾股定理, 得甲, 乙两人间的距离为:
S=,
∴当t=(在0【点睛】
本题考查二次函数的实际应用,关键在于根据题意写出二次函数关系式,再利用求二次函数的最值方法求最值.
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
一、单选题(共20分)
1.关于函数,下列说法:①函数的最小值为1;②函数图象的对称轴为直线x=3;③当x≥0时,y随x的增大而增大;④当x≤0时,y随x的增大而减小,其中正确的有( )个.
A.1 B.2 C.3 D.4
2.二次函数的图象如图所示,对称轴是直线.下列结论:①;②;③;④(为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.由二次函数,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大
4.三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米 B.5米 C.2米 D.7米
5.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
6.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是( )
A. B. C. D.
7.若y=(m+1)是二次函数,则m= ( )
A.-1 B.7 C.-1或7 D.以上都不对
8.把抛物线向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )
A. B.
C. D.
9.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
10.二次函数 的图像如图所示, 现有以下结论: (1) : (2) ; (3), (4) ; (5) ; 其中正确的结论有( )
A.2 个 B.3 个 C.4 个 D.5 个.
二、填空题(共40分)
11.将二次函数化成一般形式,其中二次项系数为________,一次项系数为________,常数项为________.
12.已知二次函数,当分别取时,函数值相等,则当取时,函数值为______.
13.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是_____.
14.已知关于的一元二次方程,有下列结论:
①当时,方程有两个不相等的实根;
②当时,方程不可能有两个异号的实根;
③当时,方程的两个实根不可能都小于1;
④当时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为_________.
15.如图,抛物线y=﹣x2+x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
16.如图有一抛物线形的拱桥,拱高10米,跨度为40米,则该抛物线的表达式为______________.
17.抛物线的图象和轴有交点,则的取值范围是______.
三、解答题(共60分)
18.如图所示,抛物线的对称轴为直线,抛物线与轴交于、两点,与轴交于点.
(1)求抛物线的解析式;
(2)连结,在第一象限内的抛物线上,是否存在一点,使的面积最大?最大面积是多少?
19.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年5月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为4000元,有客人入住的房间,宾馆每天每间另外还需支出36元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠.
(1)求入住房间z(间)与定价x(元/间)之间关系式;
(2)应将房间定价确定为多少元时,获得利润最大?求出最大利润?
20.在平面直角坐标系中,抛物线的对称轴为.
求的值及抛物线与轴的交点坐标;
若抛物线与轴有交点,且交点都在点,之间,求的取值范围.
21.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,抛物线经过、两点;
(1)求抛物线的解析式;
(2)点为轴上一点,点为直线上一点,过作交轴于点,当四边形为菱形时,请直接写出点坐标;
(3)在(2)的条件下,且点在线段上时,将抛物线向上平移个单位,平移后的抛物线与直线交于点(点在第二象限),点为轴上一点,若,且符合条件的点恰好有2个,求的取值范围.
22.如图,在平面直角坐标系中,已知抛物线与轴交于,两点,与轴交于点,连接.
(1)求抛物线的解析式;
(2)点在抛物线的对称轴上,当的周长最小时,点的坐标为_____________;
(3)点是第四象限内抛物线上的动点,连接和.求面积的最大值及此时点的坐标;
(4)若点是对称轴上的动点,在抛物线上是否存在点,使以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
23.如图是两条互相垂直的街道, 且A到B, C的距离都是4千米. 现甲从B地走向A地, 乙从A地走向C地, 若两人同时出发且速度都是4千米/时, 问何时两人之间的距离最近
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【解析】
【分析】
根据所给函数的顶点式得出函数图象的性质从而判断选项的正确性.
【详解】
解:∵,
∴该函数图象开口向上,有最小值1,故①正确;
函数图象的对称轴为直线,故②错误;
当x≥0时,y随x的增大而增大,故③正确;
当x≤﹣3时,y随x的增大而减小,当﹣3≤x≤0时,y随x的增大而增大,故④错误.
故选:B.
【点睛】
本题考查二次函数的性质,解题的关键是能够根据函数解析式分析出函数图象的性质.
2.C
【解析】
【分析】
①由抛物线开口方向得到,对称轴在轴右侧,得到与异号,又抛物线与轴正半轴相交,得到,可得出,选项①错误;
②把代入中得,所以②正确;
③由时对应的函数值,可得出,得到,由,,,得到,选项③正确;
④由对称轴为直线,即时,有最小值,可得结论,即可得到④正确.
【详解】
解:①∵抛物线开口向上,∴,
∵抛物线的对称轴在轴右侧,∴,
∵抛物线与轴交于负半轴,
∴,
∴,①错误;
②当时,,∴,
∵,∴,
把代入中得,所以②正确;
③当时,,∴,
∴,
∵,,,
∴,即,所以③正确;
④∵抛物线的对称轴为直线,
∴时,函数的最小值为,
∴,
即,所以④正确.
故选C.
【点睛】
本题考查了二次函数图象与系数的关系:二次项系数决定抛物线的开口方向和大小.当时,抛物线向上开口;当时,抛物线向下开口;一次项系数和二次项系数共同决定对称轴的位置:当与同号时,对称轴在轴左;当与异号时,对称轴在轴右.常数项决定抛物线与轴交点:抛物线与轴交于.抛物线与轴交点个数由判别式确定:时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.
3.C
【解析】
【分析】
根据二次函数的性质,直接根据的值得出开口方向,再利用顶点坐标的对称轴和增减性,分别分析即可.
【详解】
解:由二次函数,可知:
.,其图象的开口向上,故此选项错误;
.其图象的对称轴为直线,故此选项错误;
.其最小值为1,故此选项正确;
.当时,随的增大而减小,故此选项错误.
故选:.
【点睛】
此题主要考查了二次函数的性质,同学们应根据题意熟练地应用二次函数性质,这是中考中考查重点知识.
4.B
【解析】
【分析】
根据题意,可以画出相应的抛物线,然后即可得到大孔所在抛物线解析式,再求出顶点为A的小孔所在抛物线的解析式,将x=﹣10代入可求解.
【详解】
解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=-,
∴大孔所在抛物线解析式为y=-x2+,设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为-7,
∴点E坐标为(-7,-),
∴-=m(x﹣b)2,
∴x1=+b,x2=-+b,
∴MN=4,
∴|+b-(-+b)|=4
∴m=-,
∴顶点为A的小孔所在抛物线的解析式为y=-(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=-10时,y=-,
∴-=-(x﹣b)2,
∴x1=+b,x2=-+b,
∴单个小孔的水面宽度=|(+b)-(-+b)|=5(米),
故选:B.
【点睛】
本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.
5.D
【解析】
【分析】
设二次函数的解析式为:y=ax2+bx+c,根据题意列方程组即可得到结论.
【详解】
解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,y=1800,当x=75,y=1800,当x=80时,y=1550,
∴,
解得a= 2,b=260,c= 6450,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
【点睛】
本题考查了根据实际问题列二次函数关系式,正确的列方程组是解题的关键.
6.A
【解析】
【分析】
本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y的表达式,结合选项的图象可得答案.
【详解】
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
【点睛】
本题考查了动点问题的函数图象,正确地写出函数解析式并数形结合分析是解题的关键.
7.B
【解析】
【分析】
令x的指数为2,系数不为0,列出方程与不等式解答即可.
【详解】
由题意得:m2-6m-5=2;且m+1≠0;
解得m=7或-1;m≠-1,
∴m=7,
故选:B.
【点睛】
利用二次函数的定义,二次函数中自变量的指数是2;二次项的系数不为0.
8.D
【解析】
【分析】
直接根据“左加右减,上加下减”的原则进行解答即可.
【详解】
由“左加右减”的原则可知,抛物线y=2x2向右平移2个单位所得抛物线是y=2(x 2)2;
由“上加下减”的原则可知,抛物线y=2(x 2)2向下平移1个单位所得抛物线是y=2(x 2)2 1.
故选D.
【点睛】
本题考查了二次函数图象与几何变换,解题的关键是掌握二次函数图象与几何变换.
9.C
【解析】
【分析】
分别求出t=1、3、24、10时h的值可判断A、B、D三个选项,将解析式配方成顶点式可判断C选项.
【详解】
解:A、当t=1时,h=24;当t=3时,h=64;所以点火后1s和点火后3s的升空高度不相同,此选项错误;
B、当t=24时,h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、由h=﹣t2+24t+1=﹣(t-12)2+145知火箭升空的最大高度为145m,此选项正确;
D、当t=10时,h=141m,此选项错误;
故选:C.
【点睛】
本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
10.C
【解析】
【分析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【详解】
解:(1)∵函数开口向下,∴a<0,∵对称轴在y轴的右边,∴,∴b>0,故命题正确;
(2)∵a<0,b>0,c>0,∴abc<0,故命题正确;
(3)∵当x=-1时,y<0,∴a-b+c<0,故命题错误;
(4)∵当x=1时,y>0,∴a+b+c>0,故命题正确;
(5)∵抛物线与x轴于两个交点,∴b2-4ac>0,故命题正确;
故选C.
【点睛】
本题考查了二次函数图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.
11.
【解析】
【分析】
通过去括号,移项,可以把方程化成二次函数的一般形式,然后确定二次项系数,一次项系数,常数项.
【详解】
y=﹣2(x﹣2)2变形为:y=﹣2x2+8x﹣8,所以二次项系数为﹣2;一次项系数为8;常数项为﹣8.
故答案为﹣2,8,﹣8.
【点睛】
本题考查的是二次函数的一般形式,通过去括号,移项,合并同类项,得到二次函数的一般形式,确定二次项系数,一次项系数,常数项的值.
12.2020
【解析】
【分析】
根据二次函数y=2x2+2020,当x分别取x1,x2(x1≠x2)时,函数值相等,可以得到x1和x2的关系,从而可以得到2x1+2x2的值,进而可以求得当x取2x1+2x2时,函数的值.
【详解】
解:∵二次函数y=2x2+2020,当x分别取x1,x2(x1≠x2)时,函数值相等,
∴2x12+2020=2x22+2020,
∴x1=-x2,
∴2x1+2x2=2(x1+x2)=0,
∴当x=2x1+2x2时,y=2×0+2020=0+2020=2020,
故答案为:2020.
【点睛】
本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
13.﹣3<x<1
【解析】
【分析】
根据抛物线与x轴的一个交点坐标和对称轴,由抛物线的对称性可求抛物线与x轴的另一个交点,再根据抛物线的增减性可求当y<0时,x的取值范围.
【详解】
解:∵抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为(﹣3,0),对称轴为x=﹣1,
∴抛物线与x轴的另一个交点为(1,0),
由图象可知,当y<0时,x的取值范围是﹣3<x<1.
故答案为:﹣3<x<1.
【点睛】
本题考查了二次函数的性质和数形结合能力,熟练掌握并灵活运用是解题的关键.
14.①③④
【解析】
【分析】
由根的判别式,根与系数的关系进行判断,即可得到答案.
【详解】
解:根据题意,∵一元二次方程,
∴;
∴当,即时,方程有两个不相等的实根;故①正确;
当,解得:,方程有两个同号的实数根,则当时,方程可能有两个异号的实根;故②错误;
抛物线的对称轴为:,则当时,方程的两个实根不可能都小于1;故③正确;
由,则,解得:或;故④正确;
∴正确的结论有①③④;
故答案为:①③④.
【点睛】
本题考查了二次函数的性质,一元二次方程根的判别式,根与系数的关系,解题的关键是掌握所学的知识进行解题.
15.2
【解析】
【分析】
利用二次函数图象上点的坐标特征可求出点A,B,C,D的坐标,由点A,D的坐标,利用待定系数法可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点E的坐标,再利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可求出线段PQ的长.
【详解】
解:当y=0时,﹣x2+x+2=0,
解得:x1=﹣2,x2=4,
∴点A的坐标为(﹣2,0);
当x=0时,y=﹣x2+x+2=2,
∴点C的坐标为(0,2);
当y=2时,﹣x2+x+2=2,
解得:x1=0,x2=2,
∴点D的坐标为(2,2).
设直线AD的解析式为y=kx+b(k≠0),
将A(﹣2,0),D(2,2)代入y=kx+b,得:
解得:
∴直线AD的解析式为y=x+1.
当x=0时,y=x+1=1,
∴点E的坐标为(0,1).
当y=1时,﹣x2+x+2=1,
解得:x1=1﹣,x2=1+,
∴点P的坐标为(1﹣,1),点Q的坐标为(1+,1),
∴PQ=1+﹣(1﹣)=2.
故答案为:2.
【点睛】
本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,利用二次函数图象上点的坐标特征求出点P,Q的坐标是解题的关键.
16.
【解析】
【分析】
由题意抛物线过点(40,0),顶点坐标为(20,10),设抛物线的解析式为,从而求出a的值,然后确定抛物线的解析式.
【详解】
解:依题意得此函数解析式顶点为,
∴设解析式为,
又函数图象经过,
,
,
.
故答案为 .
【点睛】
本题主要考查用待定系数法确定二次函数的解析式,解题时应根据情况设抛物线的解析式从而使解题简单,此题设为顶点式比较简单.
17.且
【解析】
【分析】
由题意知,,计算求解即可.
【详解】
解:由题意知,
解得
故答案为:且.
【点睛】
本题考查了二次函数与轴的交点个数.解题的关键在于熟练掌握二次函数与轴的交点个数.
18.(1);(2)存在,当时,面积最大为16,此时点点坐标为.
【解析】
【分析】
(1)用待定系数法解答便可;
(2)设点的坐标为,连结、、.根据对称性求出点B的坐标,根据得到二次函数关系式,最后配方求解即可.
【详解】
解:(1)∵抛物线过点,
∴.
∵抛物线的对称轴为直线,
∴可设抛物线为.
∵抛物线过点,
∴,解得.
∴抛物线的解析式为,即.
(2)存在,设点的坐标为,连结、、.
∵点A、关于直线对称,且
∴.
∴
.
∵
∴当时,面积最大为16,此时点点坐标为.
【点睛】
本题主要考查了二次函数的图象与性质,待定系数法,三角形面积公式以及二次函数的最值求法,根据图形得出由此得出二次函数关系式是解答此题的关键.
19.(1)z=﹣x+122(x≥168);(2)应将房间定价确定为260元时,获得利润最大,最大利润为8767元
【解析】
【分析】
(1)入住房间z(间)等于80减去每天的房间空闲数,列式并化简即可;
(2)设利润为w元,由题意得w关于x的二次函数关系式,根据二次函数的对称性及问题实际可得答案.
【详解】
解:(1)由题意得:
z=80﹣(x﹣42)
=﹣x+122,
∴入住房间z(间)与定价x(元/间)之间关系式为z=﹣x+122(x≥168);
(2)设利润为w元,由题意得:
w=(﹣x+122)x﹣36(﹣x+122)﹣4000
=﹣x2+131x﹣8392,
当x=﹣=262时,w最大,此时z=56.5非整数,不合题意,
∴x=260或264时,w最大,
∵让客人得到实惠,
∴x=260,
∴w最大==﹣×2602+131×260﹣8392=8767,
∴应将房间定价确定为260元时,获得利润最大,最大利润为8767元.
【点睛】
本题考查了二次函数在实际问题中的应用,理清题中的数量关系、熟练掌握二次函数的性质是解题的关键.
20.(1) a=-1;坐标为,;(2).
【解析】
【分析】
(1)利用抛物线的对称轴方程得到x=-=-1,解方程求出a即可得到抛物线的解析式为y=-x2-2x;然后解方程-x2-2x=0可得到抛物线与x轴的交点坐标;
(2)抛物线y=-x2-2x+m由抛物线y=-x2-2x上下平移|m|和单位得到,利用函数图象可得到当x=1时,y<0,即-1-2+m<0;当x=-1时,y≥0,即-1+2+m≥0,然后解两个不等式求出它们的公共部分可得到m的范围.
【详解】
根据题意得,解得,
所以抛物线的解析式为,
当时,,解得,,
所以抛物线与轴的交点坐标为,;
抛物线抛物线由抛物线上下平移和单位得到,而抛物线的对称轴为直线,
∵抛物线与轴的交点都在点,之间,
∴当时,,即,解得;
当时,,即,解得,
∴的取值范围为.
【点睛】
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象的几何变换.
21.(1);(2);;(3)
【解析】
【分析】
(1)由题意易得,,然后代入抛物线解析式进行求解即可;
(2)由题意可画出图象,设点,然后求出直线AB的解析式为,则可设点,点,进而根据中点坐标公式及两点距离公式可进行求解;
(3)过作轴交于,由(2)可得:,,则有,设,,进而可得,则,然后可得,则有,最后根据一元二次方程根的判别式可进行求解.
【详解】
解:(1)∵直线与轴、轴分别交于、两点,
∴,,
∵抛物线经过、两点,
∴,解得:,
∴抛物线的解析式为;
(2)由(1)可得,,由题意可得如图所示:
设点,直线AB的解析式为,把点A、B代入得:
,解得:,
∴直线AB的解析式为,
设点,点,
∵四边形是菱形,
∴根据中点坐标公式可得:,即,
∴,
∵,
∴根据两点距离公式可得:,
解得:或或(不符合题意,舍去),
∴;;
(3)过作轴交于,如图所示:
由(2)可得:,,
∴,
设,,
∵,
∴,
∴,
,
∵,,
∴,
∴,
∴,
∴,即,
化简得:,
当方程有唯一实根时,满足条件的只有一个,
∴,
化简得:,
解得:,(含去)
∴,
设平移后的抛物线为:,将点坐标代入平移后解析式得:
,
解得:,
.
【点睛】
本题主要考查二次函数的综合及相似三角形的性质与判定,熟练掌握二次函数的综合及相似三角形的性质与判定是解题的关键.
22.(1);(2);(3)面积最大为,点坐标为;(4)存在点,使以点、、、为顶点的四边形是平行四边形,,点坐标为,,.
【解析】
【分析】
(1)将点,代入即可求解;
(2)BC与对称轴的交点即为符合条件的点,据此可解;
(3)过点作轴于点,交直线与点,当EF最大时面积的取得最大值,据此可解;
(4)根据平行四边形对边平行且相等的性质可以得到存在点N使得以B,C,M,N为顶点的四边形是平行四边形.分三种情况讨论.
【详解】
解:(1) 抛物线过点,
解得:
抛物线解析式为.
(2) 点,
∴抛物线对称轴为直线
点在直线上,点,关于直线对称
,
当点、、在同一直线上时,最小.
抛物线解析式为,
∴C(0,-6),
设直线解析式为
,
解得:
直线:
,
,
故答案为:.
(3)过点作轴于点,交直线与点,
设,则
,
当时,面积最大为
,
此时点坐标为.
(4)存在点,使以点、、、为顶点的四边形是平行四边形.
设N(x,y),M(,m),
①四边形CMNB是平行四边形时,CM∥NB,CB∥MN,
,
∴x= ,
∴y= = ,
∴N(,);
②四边形CNBM是平行四边形时,CN∥BM,CM∥BN,
,
∴x=,
∴y==
∴N(,);
③四边形CNMB是平行四边形时,CB∥MN,NC∥BM,
,
∴x=,
∴y==
∴N(,);
点坐标为(,),(,),(,).
【点睛】
本题考查二次函数与几何图形的综合题,熟练掌握二次函数的性质,灵活运用数形结合思想得到坐标之间的关系是解题的关键.
23.当t=(在0
【分析】
设两人均出发了t时,根据勾股定理建立甲、乙之间的距离与时间t的函数关系式,然后求出二次函数在一定的取值范围内的最值即可得解.
【详解】
设两人均出发了t时, 则此时甲到A地的距离是(4-4t)千米, 乙离A地的距离是4t千米, 由勾股定理, 得甲, 乙两人间的距离为:
S=,
∴当t=(在0
本题考查二次函数的实际应用,关键在于根据题意写出二次函数关系式,再利用求二次函数的最值方法求最值.
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
