2022—2023学年北师大版数学九年级下册第二章 二次函数 单元测试(word、含答案)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级下册第二章 二次函数 单元测试(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 498.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 17:00:53 | ||
图片预览


文档简介
数学九年级(下册)
单元测试——二次函数
(满分 120 分)
一、选择题(每题3 分,共30 分)
1.y=2x 向上平移3个单位后所得抛物线的解析式是( )
A. y =2x +3 B. y=2(x+3)
C. y=2(x-3) D. y=2x -3
2.抛物线y= -(x+2) -3 的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
3.若二次函数y=x +m的图象经过原点,则m的值必为( )
A.0或2 B. 0 C. 2 D.-2
4.在下列二次函数中,其图象对称轴为直线x=-2的是( )
A. y=(x+2) B.y=2x -2
C. y= -2x -2 D.y=2(x-2)
5.抛物线y=x +x+1与x轴的交点个数是( )
A.0个 B.1个 C.2个 D.3个
6.抛物线y=2x +3x+4与y轴的交点为( )
A.(0,4) B.(0,2) C.(0,3) D. (0,0)
7.二次函数y=(x+2) -1的图象大致为 .
8.函数y=3x +1的最小值为( )
A .0. B.1 C.2 D.3
9.已知(-1,y)(1,y2)在抛物线y=(x+1) 的图象上,则y,与y2的大小关系为 ( )
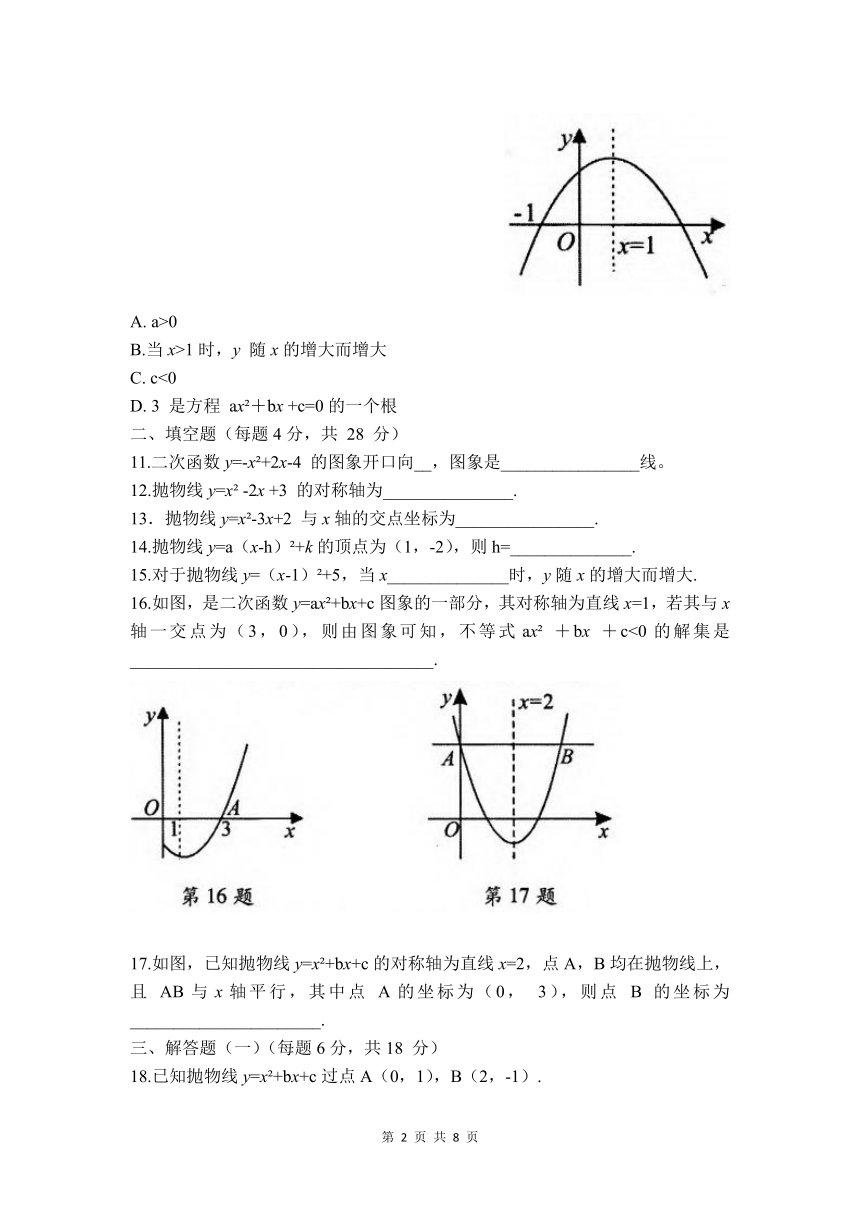
A. y1>y2 B.y1=y2 C. y110.二次函数y=αx +bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A. a>0
B.当x>1时,y 随x的增大而增大
C. c<0
D. 3 是方程 ax +bx +c=0的一个根
二、填空题(每题4分,共 28 分)
11.二次函数y=-x +2x-4 的图象开口向__,图象是________________线。
12.抛物线y=x -2x +3 的对称轴为_______________.
13.抛物线y=x -3x+2 与x轴的交点坐标为________________.
14.抛物线y=a(x-h) +k的顶点为(1,-2),则h=______________.
15.对于抛物线y=(x-1) +5,当x______________时,y随x的增大而增大.
16.如图,是二次函数y=ax +bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为(3,0),则由图象可知,不等式ax +bx +c<0的解集是___________________________________.
17.如图,已知抛物线y=x +bx+c的对称轴为直线x=2,点A,B均在抛物线上,且 AB与x轴平行,其中点 A的坐标为(0, 3),则点 B 的坐标为______________________.
三、解答题(一)(每题6分,共18 分)
18.已知抛物线y=x +bx+c过点A(0,1),B(2,-1).
(1)求抛物线的解析式;
(2)点(1,4)是否在此抛物线上
19.已知抛物线y=x -6x+5.
(1)求它与x轴的交点坐标;
(2)求它的顶点坐标.
20.已知抛物线y=x +(m+1)x+3与x轴只有一个交点,求 m的值.
四、解答题(二) (每题8分,共 24 分)
21.如图,球的飞行路线是一条抛物线,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t.
(1)球经过多少秒飞行高度达到15 m
(2)球从飞出到落地所需要的时间.
(3)球经过____ 秒飞行高度达到最高.
22.已知抛物线y=x -4x +3.
(1)该抛物线的对称 轴是__________,顶点坐标是________________;
(2)选取适当的数据填入下表,并在下图的直角坐标系内描点画出该抛物线的图象:
x … …
y … …
(3)观察图象,当x为何值时y <0
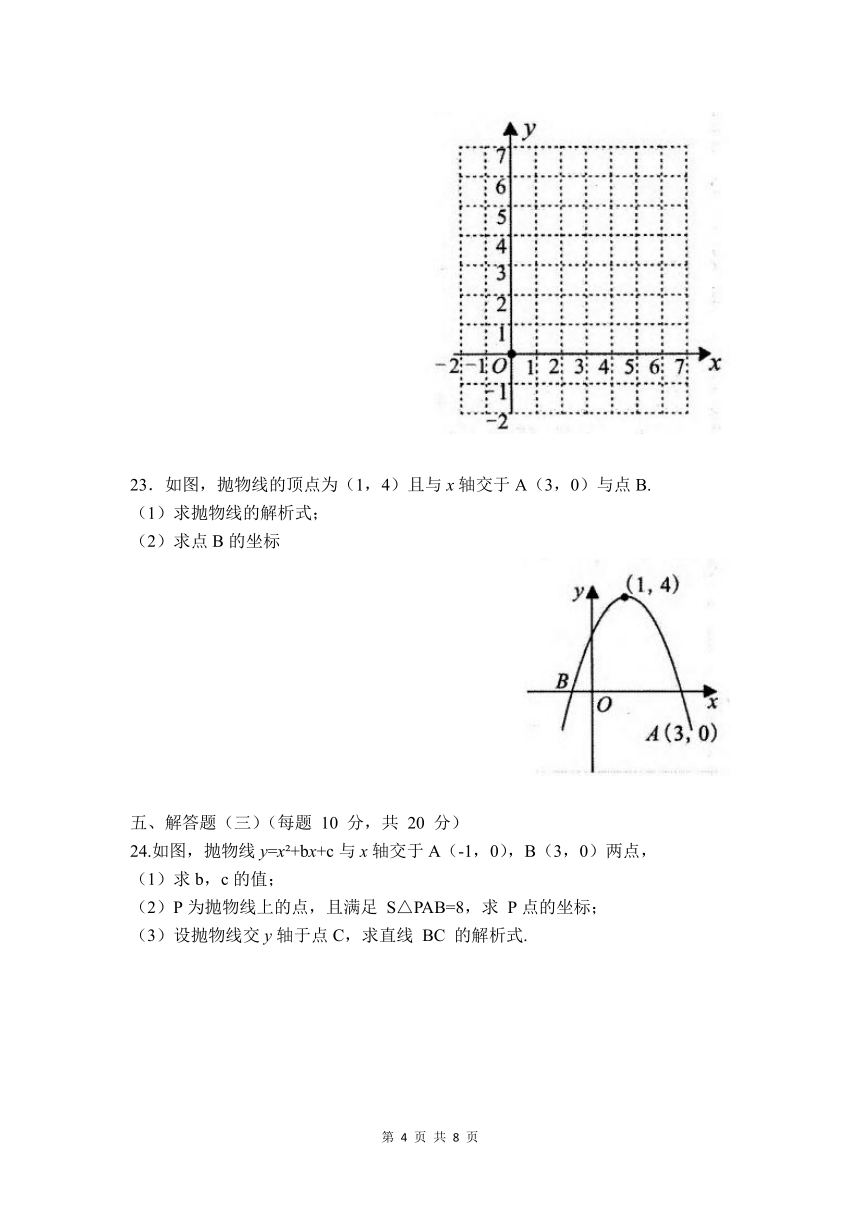
23.如图,抛物线的顶点为(1,4)且与x轴交于A(3,0)与点B.
(1)求抛物线的解析式;
(2)求点B的坐标
五、解答题(三)(每题 10 分,共 20 分)
24.如图,抛物线y=x +bx+c与x轴交于A(-1,0),B(3,0)两点,
(1)求b,c的值;
(2)P为抛物线上的点,且满足 S△PAB=8,求 P点的坐标;
(3)设抛物线交y轴于点C,求直线 BC 的解析式.
25.如图,D,E,F是 Rt△ABC三边上的点,且四边形 CDEF为矩形,BC=6,∠A =30°.
(1)求AB 的长;
(2)设AE=x,则DE=_________,EF=______________(用含x的表达式表示);
(3)求矩形 CDEF 面积的最大值.
单元测试——二次函数
一、1.A 2.D 3.B 4.A 5.A 6.A 7.D 8.B 9.C 10.D
二、11.下抛物 12.直线x=1
13.(2,0)或(1,0) 14.1 15.>1 16.-1三、18.解:(1)将A(0,1),B(2,-1)代入y=x2+bx+c中得
∴
∴y=x2-3x+1
(2)当x=1时,y=1-3+1≠14,
∴点(1,4)不在此抛物线上
19.解:(1)将y=0代入y=x2-6x+5中得x2-6x+5=0
(x-5)(x-1)=0
∴x1=5,x2=1
∵与x轴的交点:(5,0),(1,0)
(2)y=x2-6x+5
=(x2-6x)+5
=(x2-6x+32)-9+5
=(x-3)2-4
∴顶点坐标为(3,-4)
20.解:∵该抛物线与x轴只有一个交点
∴ =(m+1)2-4×1×3=0
∴.
四、21.解:(1)15=20t-5t2
-3=t2-4t
0= t2-4t+3
0=(t-1)(t-3)
∵t1=1,t2=3
∴当经过1 s或3 s时高度达到15 m
(2)令h=0则0=20t-5t2
t1=0,t2=4
∵需要4秒
(3)2
22.解:(1)∵y=x2-4x+3=(x-2)2-1
∴该抛物线的对称轴是直线x=2,顶点坐标是(2,-1)
故答案为直线x=2;(2,-1).
(2)列表
x … 0 1 2 3 4 …
y … 3 0 -1 0 3 …
描点、连接得抛物线y=x2-4x+3的图象如图所示
(3)∵抛物线y=x2-4x+3与x轴的交点为(1,0),(3,0)
∴当123.解:(1)∵该抛物线顶点为(1,4),设y=a(x-1)2+4
又∵过点A(3,0)代入得
0=a(3-1)2+4
-4=4a
a=-1
∴解析式为y=-(x-1)2+4
(2)当y=0时,0=-(x-1)2+4,
解得x1=3,x2=-1
∴点B的坐标为(-1,0)
五、24.解:(1)∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0)
∴,解得
∴所求抛物线的解析式为y=x2-2x-3;
(2)设点P的坐标为(x,y),由题意,得
,
∴|y|=4,
∵y=±4,
当y=4时,x2-2x-3=4,
∴,
当y=-4时x2-2x-3=-4
∵x=1,
∴当P点的坐标分别为或或(1,-4)时,S△PAB=8;
(3)当x=0时,y=-3,
∵点C的坐标为(0,-3)
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,-3)代入得
解得
∴直线BC的解析式为y=x-3.
25.解:(1)在Rt△ABC中,∠A=30°
∴AB=2BC=12;
(2)∵四边形CDEF是矩形,
∴ DE//BC
∴∠ADE=∠C=90°
∴
∴
∴
∴
故答案为:,
(3)S矩形CDEF=DE·EF
∴当时,
S最大为
单元测试——二次函数
(满分 120 分)
一、选择题(每题3 分,共30 分)
1.y=2x 向上平移3个单位后所得抛物线的解析式是( )
A. y =2x +3 B. y=2(x+3)
C. y=2(x-3) D. y=2x -3
2.抛物线y= -(x+2) -3 的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
3.若二次函数y=x +m的图象经过原点,则m的值必为( )
A.0或2 B. 0 C. 2 D.-2
4.在下列二次函数中,其图象对称轴为直线x=-2的是( )
A. y=(x+2) B.y=2x -2
C. y= -2x -2 D.y=2(x-2)
5.抛物线y=x +x+1与x轴的交点个数是( )
A.0个 B.1个 C.2个 D.3个
6.抛物线y=2x +3x+4与y轴的交点为( )
A.(0,4) B.(0,2) C.(0,3) D. (0,0)
7.二次函数y=(x+2) -1的图象大致为 .
8.函数y=3x +1的最小值为( )
A .0. B.1 C.2 D.3
9.已知(-1,y)(1,y2)在抛物线y=(x+1) 的图象上,则y,与y2的大小关系为 ( )
A. y1>y2 B.y1=y2 C. y1
A. a>0
B.当x>1时,y 随x的增大而增大
C. c<0
D. 3 是方程 ax +bx +c=0的一个根
二、填空题(每题4分,共 28 分)
11.二次函数y=-x +2x-4 的图象开口向__,图象是________________线。
12.抛物线y=x -2x +3 的对称轴为_______________.
13.抛物线y=x -3x+2 与x轴的交点坐标为________________.
14.抛物线y=a(x-h) +k的顶点为(1,-2),则h=______________.
15.对于抛物线y=(x-1) +5,当x______________时,y随x的增大而增大.
16.如图,是二次函数y=ax +bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为(3,0),则由图象可知,不等式ax +bx +c<0的解集是___________________________________.
17.如图,已知抛物线y=x +bx+c的对称轴为直线x=2,点A,B均在抛物线上,且 AB与x轴平行,其中点 A的坐标为(0, 3),则点 B 的坐标为______________________.
三、解答题(一)(每题6分,共18 分)
18.已知抛物线y=x +bx+c过点A(0,1),B(2,-1).
(1)求抛物线的解析式;
(2)点(1,4)是否在此抛物线上
19.已知抛物线y=x -6x+5.
(1)求它与x轴的交点坐标;
(2)求它的顶点坐标.
20.已知抛物线y=x +(m+1)x+3与x轴只有一个交点,求 m的值.
四、解答题(二) (每题8分,共 24 分)
21.如图,球的飞行路线是一条抛物线,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t.
(1)球经过多少秒飞行高度达到15 m
(2)球从飞出到落地所需要的时间.
(3)球经过____ 秒飞行高度达到最高.
22.已知抛物线y=x -4x +3.
(1)该抛物线的对称 轴是__________,顶点坐标是________________;
(2)选取适当的数据填入下表,并在下图的直角坐标系内描点画出该抛物线的图象:
x … …
y … …
(3)观察图象,当x为何值时y <0
23.如图,抛物线的顶点为(1,4)且与x轴交于A(3,0)与点B.
(1)求抛物线的解析式;
(2)求点B的坐标
五、解答题(三)(每题 10 分,共 20 分)
24.如图,抛物线y=x +bx+c与x轴交于A(-1,0),B(3,0)两点,
(1)求b,c的值;
(2)P为抛物线上的点,且满足 S△PAB=8,求 P点的坐标;
(3)设抛物线交y轴于点C,求直线 BC 的解析式.
25.如图,D,E,F是 Rt△ABC三边上的点,且四边形 CDEF为矩形,BC=6,∠A =30°.
(1)求AB 的长;
(2)设AE=x,则DE=_________,EF=______________(用含x的表达式表示);
(3)求矩形 CDEF 面积的最大值.
单元测试——二次函数
一、1.A 2.D 3.B 4.A 5.A 6.A 7.D 8.B 9.C 10.D
二、11.下抛物 12.直线x=1
13.(2,0)或(1,0) 14.1 15.>1 16.-1
∴
∴y=x2-3x+1
(2)当x=1时,y=1-3+1≠14,
∴点(1,4)不在此抛物线上
19.解:(1)将y=0代入y=x2-6x+5中得x2-6x+5=0
(x-5)(x-1)=0
∴x1=5,x2=1
∵与x轴的交点:(5,0),(1,0)
(2)y=x2-6x+5
=(x2-6x)+5
=(x2-6x+32)-9+5
=(x-3)2-4
∴顶点坐标为(3,-4)
20.解:∵该抛物线与x轴只有一个交点
∴ =(m+1)2-4×1×3=0
∴.
四、21.解:(1)15=20t-5t2
-3=t2-4t
0= t2-4t+3
0=(t-1)(t-3)
∵t1=1,t2=3
∴当经过1 s或3 s时高度达到15 m
(2)令h=0则0=20t-5t2
t1=0,t2=4
∵需要4秒
(3)2
22.解:(1)∵y=x2-4x+3=(x-2)2-1
∴该抛物线的对称轴是直线x=2,顶点坐标是(2,-1)
故答案为直线x=2;(2,-1).
(2)列表
x … 0 1 2 3 4 …
y … 3 0 -1 0 3 …
描点、连接得抛物线y=x2-4x+3的图象如图所示
(3)∵抛物线y=x2-4x+3与x轴的交点为(1,0),(3,0)
∴当1
又∵过点A(3,0)代入得
0=a(3-1)2+4
-4=4a
a=-1
∴解析式为y=-(x-1)2+4
(2)当y=0时,0=-(x-1)2+4,
解得x1=3,x2=-1
∴点B的坐标为(-1,0)
五、24.解:(1)∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0)
∴,解得
∴所求抛物线的解析式为y=x2-2x-3;
(2)设点P的坐标为(x,y),由题意,得
,
∴|y|=4,
∵y=±4,
当y=4时,x2-2x-3=4,
∴,
当y=-4时x2-2x-3=-4
∵x=1,
∴当P点的坐标分别为或或(1,-4)时,S△PAB=8;
(3)当x=0时,y=-3,
∵点C的坐标为(0,-3)
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,-3)代入得
解得
∴直线BC的解析式为y=x-3.
25.解:(1)在Rt△ABC中,∠A=30°
∴AB=2BC=12;
(2)∵四边形CDEF是矩形,
∴ DE//BC
∴∠ADE=∠C=90°
∴
∴
∴
∴
故答案为:,
(3)S矩形CDEF=DE·EF
∴当时,
S最大为
