2023届高三数学简易教学小专题学案之 立体几何( 最短路径)(含解析)
文档属性
| 名称 | 2023届高三数学简易教学小专题学案之 立体几何( 最短路径)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 05:17:52 | ||
图片预览

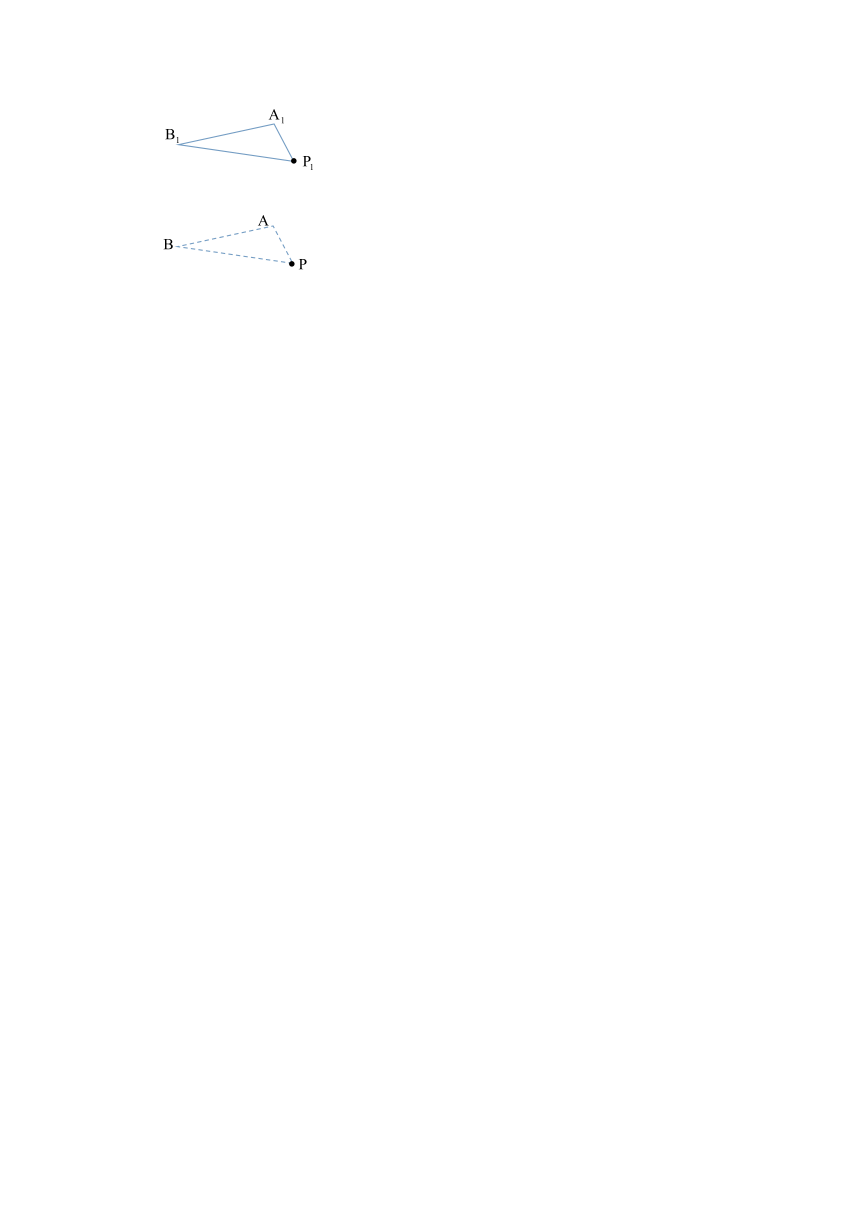

文档简介
《立体几何》专题11-1 最短路径
(5套6页含答案)
知识点:
最短路径: 把几何体各面摊开,两点之间线段最短,所以,直接连接相关两点即可。 点线之间,垂线段最短,所以,要求点线距离最值,作垂线即可。
典型例题:
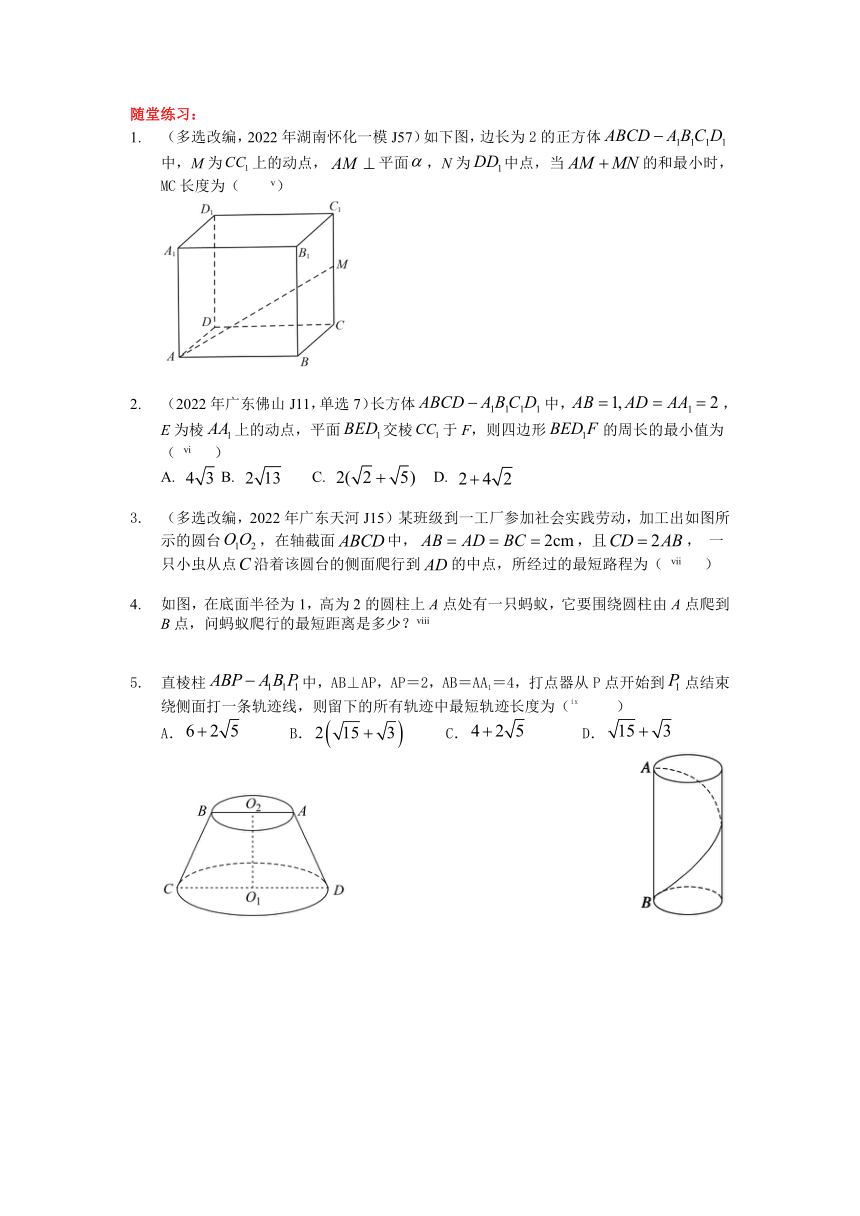
(多选改编,2022年广东梅州二模J20)在长方体中,,,动点在体对角线上(含端点),的最小值( [endnoteRef:0] )
[0: ;
【分析】当时,取得最小值,
由B得,此时,则,,
所以,
即的最小值为;
]
如图,长方体中,交于顶点的三条棱长分别为,,,则从点沿表面到的最短距离为( [endnoteRef:1] ) A. B. C. D.
[1: 答案:B;]
在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为___[endnoteRef:2]__.
[2: 答案:;]
(多选改编,2022年福建德化一中J37)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A,C的点,, 若AB=BC,E为线段AB上的动点,则SE+CE的最小值为( [endnoteRef:3] )
[3: ;
【解析】
【分析】把棱锥的两个面和摊平,利用平面上的性质求的最小值判断D.
【详解】时,把和摊平,如图,
的最小值是,此时,,,,
.
]
随堂练习:
(多选改编,2022年湖南怀化一模J57)如下图,边长为2的正方体中,M为上的动点,平面,N为中点,当的和最小时,MC长度为( [endnoteRef:4])
[4:
【分析】将矩形与矩形延展为一个平面,利用、、三点共线得知最短,利用平行线分线段成比例定理求得,可判断D选项的正误.
将矩形与矩形延展一个平面,如下图所示:
若最短,则、、三点共线,
,,
,所以,点不是棱的中点,D选项错误.]
(2022年广东佛山J11,单选7)长方体中,,E为棱上的动点,平面交棱于F,则四边形的周长的最小值为( [endnoteRef:5] )
A. B. C. D. [5: 【答案】B
【解析】
【分析】将几何体展开,利用两点之间直线段最短即可求得截面最短周长.
【详解】解:将长方体展开,如图所示:
当点为与的交点,为与的交点时,截面四边形的周长最小,
最小值为.
故选:B.
]
(多选改编,2022年广东天河J15)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台,在轴截面中,,且, 一只小虫从点沿着该圆台的侧面爬行到的中点,所经过的最短路程为( [endnoteRef:6] )
[6: ;
【详解】
将圆台一半侧面展开,如下图中,设为中点,圆台对应的圆锥一半侧面展开为扇形,
由可得,则,,又,则,
即点到的中点所经过的最短路程为.
]
如图,在底面半径为1,高为2的圆柱上A点处有一只蚂蚁,它要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?[endnoteRef:7]
[7: 答案:2;
解 把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,
∴AB′===2,
即蚂蚁爬行的最短距离为2.
]
直棱柱中,AB⊥AP,AP=2,AB=AA1=4,打点器从P点开始到点结束绕侧面打一条轨迹线,则留下的所有轨迹中最短轨迹长度为([endnoteRef:8] )
A. B. C. D.
[8: 答案:B;
]
《立体几何》专题11-2 最短路径
(多选改编,2022年广东华附三模J16)已知圆锥的顶点为P,母线长为2,底面圆直径为,A,B,C为底面圆周上的三个不同的动点,M为母线PC上一点,当AB为直径且C为弧AB的中点时,的最小值为( [endnoteRef:9] )
[9: ;
由题意可得△PAC和△PBC全等,在△PAC中,,,所以,进而,记PC边上的高为h(垂足为Q),则,所以,当M与Q重合时取等号。
]
(多选改编,2022年广东肇庆J36)已知正方体的棱长为1,点P是线段上(不含端点)的任意一点,点E是线段的中点,点F是平面ABCD内一点,的最小值是( [endnoteRef:10] )
[10: ]
有一根长为3π cm,底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,求铁丝的最短长度.([endnoteRef:11]) [11: 答案:5π cm;
解 把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图所示),由题意知BC=3π cm,AB=4π cm,点A与点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.
AC==5π cm,
故铁丝的最短长度为5π cm.
]
长方体ABCD—A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.([endnoteRef:12]) [12: 答案:解 把长方体含AC1的面作展开图,有三种情形如图所示:利用勾股定理可得AC1的长分别为、、.
由此可见图②是最短路线,其路程的最小值为.
]
如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1= ,P是BC1上一动点,则CP+PA1的最小值是______[endnoteRef:13]_____.
[13: 答案:5 ;
解析
将△BCC1沿BC1线折到面A1C1B上,如图.
连接A1C即为CP+PA1的最小值,过点C作CD⊥C1D于D点,△BCC1为等腰直角三角形,
∴CD=1,C1D=1,A1D=A1C1+C1D=7.
∴A1C===5 .
]
(多选)在棱长为1的正方体中,点M在棱上,则下列结论正确的是( [endnoteRef:14] )
A. 直线BM与平面平行 B. 平面截正方体所得的截面为三角形
C. 异面直线与所成的角为 D. 的最小值为 [14: 答案:ACD;]
《立体几何》专题11-3 最短路径
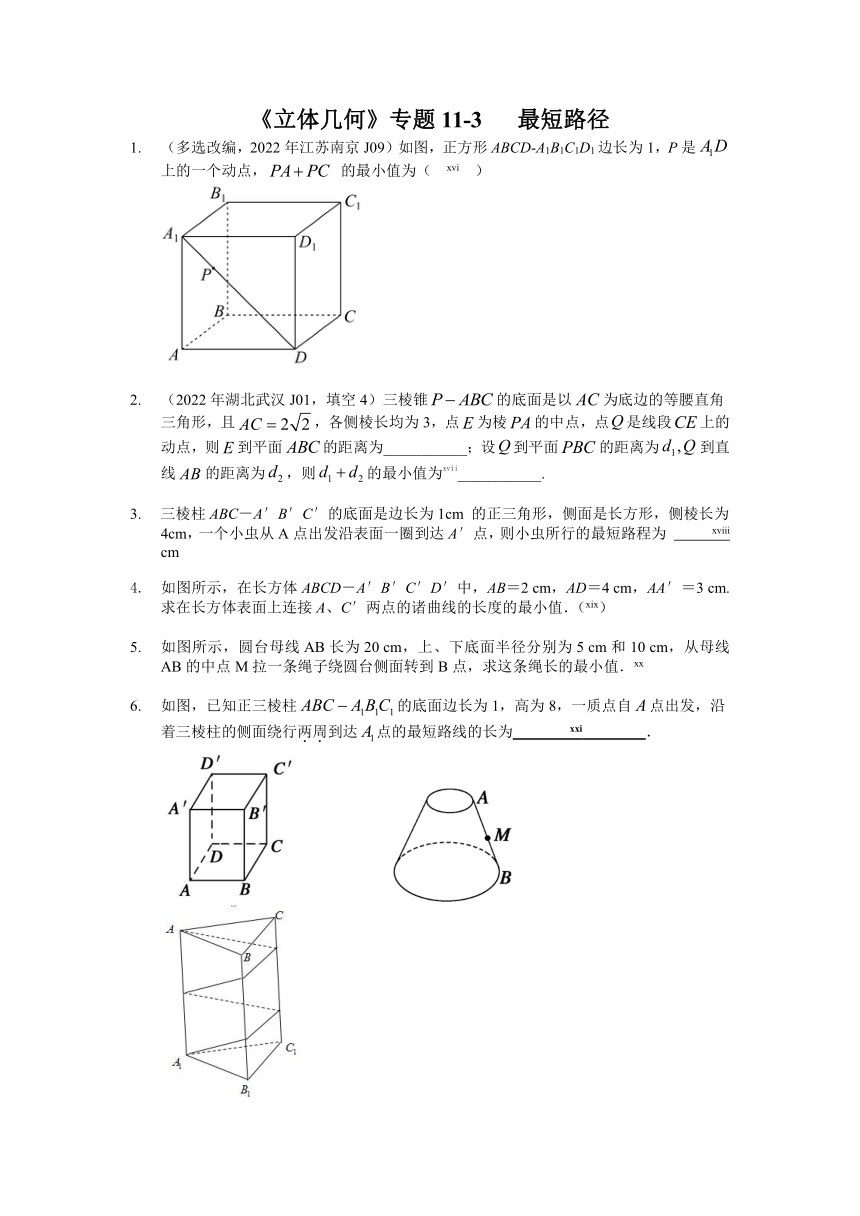
(多选改编,2022年江苏南京J09)如图,正方形ABCD-A1B1C1D1边长为1,P是 上的一个动点, 的最小值为( [endnoteRef:15] )
[15: ;
【详解】对于B,以为坐标原点建系,以 分别为x,y,z轴建立空间直角坐标系,
则,设,
,
表示平面上之间的距离,
表示平面上之间的距离,
错;
]
(2022年湖北武汉J01,填空4)三棱锥的底面是以为底边的等腰直角三角形,且,各侧棱长均为3,点为棱的中点,点是线段上的动点,则到平面的距离为___________;设到平面的距离为到直线的距离为,则的最小值为[endnoteRef:16]___________.
[16: 【答案】 ①. ## ②. ##
【解析】
【分析】取中点,连接,通过得出平面可求出到平面的距离,以为原点建立空间直角坐标系设,利用向量关系表示出,求导可求出最小值.
【详解】取中点,连接,
因,,所以,且,
因为是等腰直角三角形,所以,且,
又,满足,所以,
因为,所以平面,
因为点为棱的中点,所以到平面的距离为;
如图,以为原点建立空间直角坐标系,设,
则,
则,
设,则可得,
则,则,
所以,
所以,
所以,
设平面的法向量为,
则,即,令,可得,
则,
所以,
所以,令,解得,
又,所以在单调递增,
所以当时,,单调递减,当时,,单调递增,
所以,即的最小值为.
故答案为:;.
]
三棱柱ABC-A′B′C′的底面是边长为1cm 的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达A′点,则小虫所行的最短路程为 [endnoteRef:17] cm [17: 答案:5;]
如图所示,在长方体ABCD-A′B′C′D′中,AB=2 cm,AD=4 cm,AA′=3 cm.求在长方体表面上连接A、C′两点的诸曲线的长度的最小值.([endnoteRef:18])
[18: 答案: cm;
[解析] 将长方体的表面展开为平面图,这就将原问题转化为平面问题.本题所求必在下图所示的三个图中,从而,连接AC′的诸曲线中长度最小的为 cm(如图乙所示).
]
如图所示,圆台母线AB长为20 cm,上、下底面半径分别为5 cm和10 cm,从母线AB的中点M拉一条绳子绕圆台侧面转到B点,求这条绳长的最小值.[endnoteRef:19]
[19: 答案:50 cm;
解 作出圆台的侧面展开图,如图所示,由其轴截面中Rt△OPA与Rt△OQB相似,得=,可求得OA=20 cm.设∠BOB′=α,由于扇形弧的长与底面圆Q的周长相等,而底面圆Q的周长为2π×10 cm.扇形OBB′的半径为OA+AB=20+20=40 cm,扇形OBB′所在圆的周长为2π×40=80π cm.所以扇形弧的长度20π为所在圆周长的.所以OB⊥OB′.所以在Rt△B′OM中,B′M2=402+302,
所以B′M=50 cm,即所求绳长的最小值为50 cm.
]
如图,已知正三棱柱的底面边长为1,高为8,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为 [endnoteRef:20] .
[20: 答案:10;]
《立体几何》专题11-4 最短路径
(2022年山东历城二中J01,填空4)如图,在长方体中,,,E为线段的中点,F是棱上的动点,若点P为线段上的动点,则的最小值为[endnoteRef:21]______.
[21: 【16题答案】
【答案】2
【解析】
【分析】连接,得出点、、在平面中,问题转化为在平面内直线上取一点,求点到定点的距离与到定直线的距离的和的最小值问题,建立平面直角坐标系,求出点关于直线的对称点的坐标,则答案可求.
【详解】连接,则,点、、在平面中,
且,,,
如图1所示;在△中,以为轴,为轴,建立平面直角坐标系,
如图2所示,则,,;
设点关于直线的对称点为,
的方程为,①
,直线的方程为,②
由①②组成方程组,解得,,
直线与的交点,.
对称点,
.
则的最小值为2.
故答案为:2.
]
(2022年湖南师大附中J15,填空4)在侧棱长为2的正三棱锥中,,,两两垂直, 分别为 的中点,则三棱锥的外接球的表面积为___________,若为上的动点,是平面上的动点,则的最小值是[endnoteRef:22]___________.
[22: 【答案】
【分析】由三角形ADC与AEC为直角三角形,可得斜边AC中点M即为三棱锥的外接球球心,从而即可求解;当最小时,平面,则Q在线段DG上,将三角形沿翻折,使之与三角形共面,从而即可计算最短距离.
【详解】解:因为DA ,DB,DC两两垂直,,
所以,因为M,E分别为AC、AB的中点,
所以,
所以,故M为三棱锥的外接球球心,
所以三棱锥的外接球的表面积;
在正三棱锥中,E为AB中点,
,平面,
设CE中点为G,连接,
为AC中点,且M G=A E=,
平面,
∴即为在平面上的射影,
当最小时,平面,故Q在线段DG上.
如图,将三角形沿翻折,使之与三角形共面,
此时,的最小值,即为点到的距离,
过点作于点,
又,
,
,
,
故答案为:.
]
边长为5cm的正方形EFGH是圆柱的轴截面,则从正点沿圆柱的侧面到相对顶点G的最短距离是( [endnoteRef:23] )
A.10cm B.5cm C.5cm D.cm [23: 答案:D;]
如图,在三棱柱中,底面,∠ACB=90°,为上的动点,则的最小值为( [endnoteRef:24] ) A. B. C.5 D. [24: 答案:C;
由题设知△为等腰直角三角形,又平面,
故∠=90°,将二面角沿展开成平面图形,
得四边形如图示,由此,要取得最小值,
当且仅当三点共线,由题设知∠,
由余弦定理得.]
某圆柱的高为2,底面周长为16,A点在左侧上方,B点在下面中间圆周上,则在此圆柱侧面上,从A到B的路径中,最短路径的长度为([endnoteRef:25] )
A. B. C.3 D.2
[25: 答案:B;
【解析】由题意可知几何体是圆柱,底面周长16,高为:2,
直观图以及侧面展开图如图:
圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.
故选:B.]
在三棱锥P-ABC中,AP,AB,AC两两垂直,且AP=AB=AC=,若点D,E分别在棱PB,PC上移动(都不含端点),则AD+DE+EA的最小值为[endnoteRef:26]
[26: 答案:;]
《立体几何》专题11-5 最短路径
(多选改编,2022年江苏常州J59)棱长为1的正方体中,点P为线段上的动点,点M,N分别为线段,的中点,的最小值为( [endnoteRef:27] )
[27: ;
【分析】结合C可判断D.
选项D,
,当时,的最小值为.]
(多选改编,2022年湖北考协J49)如图,直三棱柱中,平面平面,D F分别是 的中点,点E为上动点,若,,则与长度之和最小值为( [endnoteRef:28] )
[28: ;
【详解】若,与长度和最小时,可展开平面(如图),
当平面与平面共面,且三点共线时,长度和最小.
如图,不难知,.
由由余弦定理,,
所以,即长度之和最小值为.
]
(多选改编,2022年福建漳州一中J21)如图,已知圆锥的轴截面PAB为等腰直角三角形,底面圆O的直径为2.C是圆O上异于A,B的一点,D为弦AC的中点,E为线段PB上异于P,B的点,若,则的最小值为( [endnoteRef:29] )
[29: ;
【详解】在三棱锥中,将侧面PBC绕PB旋转至平面,使之与平面PAB共面,如图所示,
则当A,E,共线时,取得最小值,
因为,,所以,
由余弦定理可得,即的最小值为.
]
长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到C′的最短矩离
是 [endnoteRef:30] [30: 答案:5;]
(多选4,2022年广东茂名J03)已知正方体的棱长为2,M为棱上的动点,平面,若为中点,当最小时,( [endnoteRef:31]) [31: ;
【解答】解:对于选项,将矩形与矩形延展为一个平面,如下图所示:
若最短,则、、三点共线,
,,,
所以,选项正确;
]
圆锥底面半径为1,高为,点P是底面圆周上一点,则一动点从点P出发,绕圆锥侧面一圈之后回到点P,则绕行的最短距离是[endnoteRef:32] .
[32: 答案:;]
(5套6页含答案)
知识点:
最短路径: 把几何体各面摊开,两点之间线段最短,所以,直接连接相关两点即可。 点线之间,垂线段最短,所以,要求点线距离最值,作垂线即可。
典型例题:
(多选改编,2022年广东梅州二模J20)在长方体中,,,动点在体对角线上(含端点),的最小值( [endnoteRef:0] )
[0: ;
【分析】当时,取得最小值,
由B得,此时,则,,
所以,
即的最小值为;
]
如图,长方体中,交于顶点的三条棱长分别为,,,则从点沿表面到的最短距离为( [endnoteRef:1] ) A. B. C. D.
[1: 答案:B;]
在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为___[endnoteRef:2]__.
[2: 答案:;]
(多选改编,2022年福建德化一中J37)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A,C的点,, 若AB=BC,E为线段AB上的动点,则SE+CE的最小值为( [endnoteRef:3] )
[3: ;
【解析】
【分析】把棱锥的两个面和摊平,利用平面上的性质求的最小值判断D.
【详解】时,把和摊平,如图,
的最小值是,此时,,,,
.
]
随堂练习:
(多选改编,2022年湖南怀化一模J57)如下图,边长为2的正方体中,M为上的动点,平面,N为中点,当的和最小时,MC长度为( [endnoteRef:4])
[4:
【分析】将矩形与矩形延展为一个平面,利用、、三点共线得知最短,利用平行线分线段成比例定理求得,可判断D选项的正误.
将矩形与矩形延展一个平面,如下图所示:
若最短,则、、三点共线,
,,
,所以,点不是棱的中点,D选项错误.]
(2022年广东佛山J11,单选7)长方体中,,E为棱上的动点,平面交棱于F,则四边形的周长的最小值为( [endnoteRef:5] )
A. B. C. D. [5: 【答案】B
【解析】
【分析】将几何体展开,利用两点之间直线段最短即可求得截面最短周长.
【详解】解:将长方体展开,如图所示:
当点为与的交点,为与的交点时,截面四边形的周长最小,
最小值为.
故选:B.
]
(多选改编,2022年广东天河J15)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台,在轴截面中,,且, 一只小虫从点沿着该圆台的侧面爬行到的中点,所经过的最短路程为( [endnoteRef:6] )
[6: ;
【详解】
将圆台一半侧面展开,如下图中,设为中点,圆台对应的圆锥一半侧面展开为扇形,
由可得,则,,又,则,
即点到的中点所经过的最短路程为.
]
如图,在底面半径为1,高为2的圆柱上A点处有一只蚂蚁,它要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?[endnoteRef:7]
[7: 答案:2;
解 把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,
∴AB′===2,
即蚂蚁爬行的最短距离为2.
]
直棱柱中,AB⊥AP,AP=2,AB=AA1=4,打点器从P点开始到点结束绕侧面打一条轨迹线,则留下的所有轨迹中最短轨迹长度为([endnoteRef:8] )
A. B. C. D.
[8: 答案:B;
]
《立体几何》专题11-2 最短路径
(多选改编,2022年广东华附三模J16)已知圆锥的顶点为P,母线长为2,底面圆直径为,A,B,C为底面圆周上的三个不同的动点,M为母线PC上一点,当AB为直径且C为弧AB的中点时,的最小值为( [endnoteRef:9] )
[9: ;
由题意可得△PAC和△PBC全等,在△PAC中,,,所以,进而,记PC边上的高为h(垂足为Q),则,所以,当M与Q重合时取等号。
]
(多选改编,2022年广东肇庆J36)已知正方体的棱长为1,点P是线段上(不含端点)的任意一点,点E是线段的中点,点F是平面ABCD内一点,的最小值是( [endnoteRef:10] )
[10: ]
有一根长为3π cm,底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,求铁丝的最短长度.([endnoteRef:11]) [11: 答案:5π cm;
解 把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图所示),由题意知BC=3π cm,AB=4π cm,点A与点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.
AC==5π cm,
故铁丝的最短长度为5π cm.
]
长方体ABCD—A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.([endnoteRef:12]) [12: 答案:解 把长方体含AC1的面作展开图,有三种情形如图所示:利用勾股定理可得AC1的长分别为、、.
由此可见图②是最短路线,其路程的最小值为.
]
如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1= ,P是BC1上一动点,则CP+PA1的最小值是______[endnoteRef:13]_____.
[13: 答案:5 ;
解析
将△BCC1沿BC1线折到面A1C1B上,如图.
连接A1C即为CP+PA1的最小值,过点C作CD⊥C1D于D点,△BCC1为等腰直角三角形,
∴CD=1,C1D=1,A1D=A1C1+C1D=7.
∴A1C===5 .
]
(多选)在棱长为1的正方体中,点M在棱上,则下列结论正确的是( [endnoteRef:14] )
A. 直线BM与平面平行 B. 平面截正方体所得的截面为三角形
C. 异面直线与所成的角为 D. 的最小值为 [14: 答案:ACD;]
《立体几何》专题11-3 最短路径
(多选改编,2022年江苏南京J09)如图,正方形ABCD-A1B1C1D1边长为1,P是 上的一个动点, 的最小值为( [endnoteRef:15] )
[15: ;
【详解】对于B,以为坐标原点建系,以 分别为x,y,z轴建立空间直角坐标系,
则,设,
,
表示平面上之间的距离,
表示平面上之间的距离,
错;
]
(2022年湖北武汉J01,填空4)三棱锥的底面是以为底边的等腰直角三角形,且,各侧棱长均为3,点为棱的中点,点是线段上的动点,则到平面的距离为___________;设到平面的距离为到直线的距离为,则的最小值为[endnoteRef:16]___________.
[16: 【答案】 ①. ## ②. ##
【解析】
【分析】取中点,连接,通过得出平面可求出到平面的距离,以为原点建立空间直角坐标系设,利用向量关系表示出,求导可求出最小值.
【详解】取中点,连接,
因,,所以,且,
因为是等腰直角三角形,所以,且,
又,满足,所以,
因为,所以平面,
因为点为棱的中点,所以到平面的距离为;
如图,以为原点建立空间直角坐标系,设,
则,
则,
设,则可得,
则,则,
所以,
所以,
所以,
设平面的法向量为,
则,即,令,可得,
则,
所以,
所以,令,解得,
又,所以在单调递增,
所以当时,,单调递减,当时,,单调递增,
所以,即的最小值为.
故答案为:;.
]
三棱柱ABC-A′B′C′的底面是边长为1cm 的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达A′点,则小虫所行的最短路程为 [endnoteRef:17] cm [17: 答案:5;]
如图所示,在长方体ABCD-A′B′C′D′中,AB=2 cm,AD=4 cm,AA′=3 cm.求在长方体表面上连接A、C′两点的诸曲线的长度的最小值.([endnoteRef:18])
[18: 答案: cm;
[解析] 将长方体的表面展开为平面图,这就将原问题转化为平面问题.本题所求必在下图所示的三个图中,从而,连接AC′的诸曲线中长度最小的为 cm(如图乙所示).
]
如图所示,圆台母线AB长为20 cm,上、下底面半径分别为5 cm和10 cm,从母线AB的中点M拉一条绳子绕圆台侧面转到B点,求这条绳长的最小值.[endnoteRef:19]
[19: 答案:50 cm;
解 作出圆台的侧面展开图,如图所示,由其轴截面中Rt△OPA与Rt△OQB相似,得=,可求得OA=20 cm.设∠BOB′=α,由于扇形弧的长与底面圆Q的周长相等,而底面圆Q的周长为2π×10 cm.扇形OBB′的半径为OA+AB=20+20=40 cm,扇形OBB′所在圆的周长为2π×40=80π cm.所以扇形弧的长度20π为所在圆周长的.所以OB⊥OB′.所以在Rt△B′OM中,B′M2=402+302,
所以B′M=50 cm,即所求绳长的最小值为50 cm.
]
如图,已知正三棱柱的底面边长为1,高为8,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为 [endnoteRef:20] .
[20: 答案:10;]
《立体几何》专题11-4 最短路径
(2022年山东历城二中J01,填空4)如图,在长方体中,,,E为线段的中点,F是棱上的动点,若点P为线段上的动点,则的最小值为[endnoteRef:21]______.
[21: 【16题答案】
【答案】2
【解析】
【分析】连接,得出点、、在平面中,问题转化为在平面内直线上取一点,求点到定点的距离与到定直线的距离的和的最小值问题,建立平面直角坐标系,求出点关于直线的对称点的坐标,则答案可求.
【详解】连接,则,点、、在平面中,
且,,,
如图1所示;在△中,以为轴,为轴,建立平面直角坐标系,
如图2所示,则,,;
设点关于直线的对称点为,
的方程为,①
,直线的方程为,②
由①②组成方程组,解得,,
直线与的交点,.
对称点,
.
则的最小值为2.
故答案为:2.
]
(2022年湖南师大附中J15,填空4)在侧棱长为2的正三棱锥中,,,两两垂直, 分别为 的中点,则三棱锥的外接球的表面积为___________,若为上的动点,是平面上的动点,则的最小值是[endnoteRef:22]___________.
[22: 【答案】
【分析】由三角形ADC与AEC为直角三角形,可得斜边AC中点M即为三棱锥的外接球球心,从而即可求解;当最小时,平面,则Q在线段DG上,将三角形沿翻折,使之与三角形共面,从而即可计算最短距离.
【详解】解:因为DA ,DB,DC两两垂直,,
所以,因为M,E分别为AC、AB的中点,
所以,
所以,故M为三棱锥的外接球球心,
所以三棱锥的外接球的表面积;
在正三棱锥中,E为AB中点,
,平面,
设CE中点为G,连接,
为AC中点,且M G=A E=,
平面,
∴即为在平面上的射影,
当最小时,平面,故Q在线段DG上.
如图,将三角形沿翻折,使之与三角形共面,
此时,的最小值,即为点到的距离,
过点作于点,
又,
,
,
,
故答案为:.
]
边长为5cm的正方形EFGH是圆柱的轴截面,则从正点沿圆柱的侧面到相对顶点G的最短距离是( [endnoteRef:23] )
A.10cm B.5cm C.5cm D.cm [23: 答案:D;]
如图,在三棱柱中,底面,∠ACB=90°,为上的动点,则的最小值为( [endnoteRef:24] ) A. B. C.5 D. [24: 答案:C;
由题设知△为等腰直角三角形,又平面,
故∠=90°,将二面角沿展开成平面图形,
得四边形如图示,由此,要取得最小值,
当且仅当三点共线,由题设知∠,
由余弦定理得.]
某圆柱的高为2,底面周长为16,A点在左侧上方,B点在下面中间圆周上,则在此圆柱侧面上,从A到B的路径中,最短路径的长度为([endnoteRef:25] )
A. B. C.3 D.2
[25: 答案:B;
【解析】由题意可知几何体是圆柱,底面周长16,高为:2,
直观图以及侧面展开图如图:
圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.
故选:B.]
在三棱锥P-ABC中,AP,AB,AC两两垂直,且AP=AB=AC=,若点D,E分别在棱PB,PC上移动(都不含端点),则AD+DE+EA的最小值为[endnoteRef:26]
[26: 答案:;]
《立体几何》专题11-5 最短路径
(多选改编,2022年江苏常州J59)棱长为1的正方体中,点P为线段上的动点,点M,N分别为线段,的中点,的最小值为( [endnoteRef:27] )
[27: ;
【分析】结合C可判断D.
选项D,
,当时,的最小值为.]
(多选改编,2022年湖北考协J49)如图,直三棱柱中,平面平面,D F分别是 的中点,点E为上动点,若,,则与长度之和最小值为( [endnoteRef:28] )
[28: ;
【详解】若,与长度和最小时,可展开平面(如图),
当平面与平面共面,且三点共线时,长度和最小.
如图,不难知,.
由由余弦定理,,
所以,即长度之和最小值为.
]
(多选改编,2022年福建漳州一中J21)如图,已知圆锥的轴截面PAB为等腰直角三角形,底面圆O的直径为2.C是圆O上异于A,B的一点,D为弦AC的中点,E为线段PB上异于P,B的点,若,则的最小值为( [endnoteRef:29] )
[29: ;
【详解】在三棱锥中,将侧面PBC绕PB旋转至平面,使之与平面PAB共面,如图所示,
则当A,E,共线时,取得最小值,
因为,,所以,
由余弦定理可得,即的最小值为.
]
长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到C′的最短矩离
是 [endnoteRef:30] [30: 答案:5;]
(多选4,2022年广东茂名J03)已知正方体的棱长为2,M为棱上的动点,平面,若为中点,当最小时,( [endnoteRef:31]) [31: ;
【解答】解:对于选项,将矩形与矩形延展为一个平面,如下图所示:
若最短,则、、三点共线,
,,,
所以,选项正确;
]
圆锥底面半径为1,高为,点P是底面圆周上一点,则一动点从点P出发,绕圆锥侧面一圈之后回到点P,则绕行的最短距离是[endnoteRef:32] .
[32: 答案:;]
同课章节目录
