2022-2023学年北师大版八年级数学上册1.1 探索勾股定理 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册1.1 探索勾股定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 490.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 15:48:51 | ||
图片预览



文档简介
2022-2023学年度初中数学北师大版 八年级上册
课堂提升训练
第一章 勾股定理
1 探索勾股定理
基础过关全练
知识点1 勾股定理
1.(2022山东枣庄四中月考)下列说法正确的是( )
A.若a、b、c是△ABC的三边长,则a2+b2=c2
B.若a、b、c是Rt△ABC的三边长,则a2+b2=c2
C.若a、b、c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a、b、c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
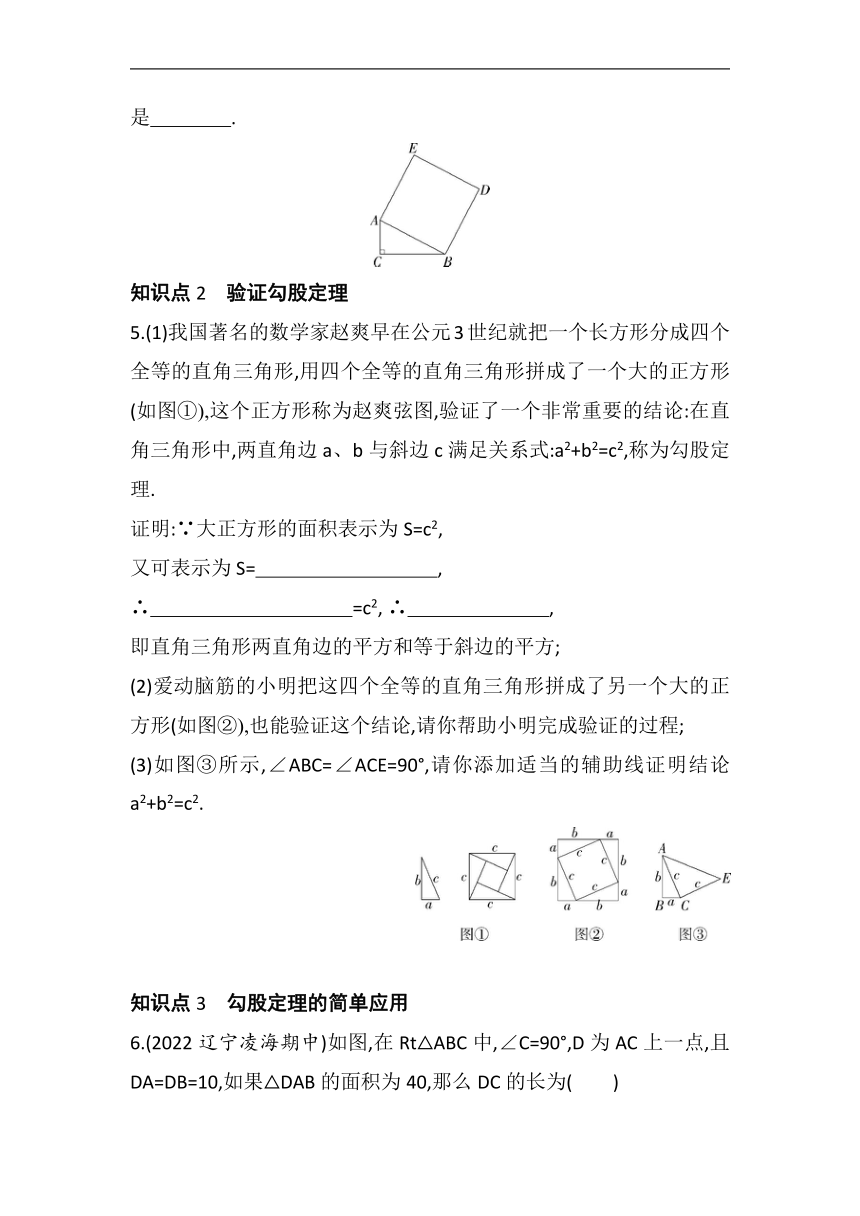
2.(2021四川资阳期末)如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( )
A.4 B.5 C.6 D.7
3.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π C.8π D.16π
4.如图,Rt△ABC中,∠C=90°,AC=5,BC=12,则正方形ABDE的面积是 .
知识点2 验证勾股定理
5.(1)我国著名的数学家赵爽早在公元3世纪就把一个长方形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图①),这个正方形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中,两直角边a、b与斜边c满足关系式:a2+b2=c2,称为勾股定理.
证明:∵大正方形的面积表示为S=c2,
又可表示为S= ,
∴ =c2, ∴ ,
即直角三角形两直角边的平方和等于斜边的平方;
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②),也能验证这个结论,请你帮助小明完成验证的过程;
(3)如图③所示,∠ABC=∠ACE=90°,请你添加适当的辅助线证明结论a2+b2=c2.
知识点3 勾股定理的简单应用
6.(2022辽宁凌海期中)如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=10,如果△DAB的面积为40,那么DC的长为( )
A.6 B.7 C.8 D.9
7.(2021四川乐山犍为期末)如图,将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中,设筷子露在杯子外面的长度是h cm,则h的取值范围是( )
A.5≤h≤12 B.12≤h≤19
C.11≤h≤12 D.12≤h≤13
8.(2022山东济南济阳期中)如图,已知钓鱼竿AC的长为10 m,露在水面上的鱼线BC长为6 m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8 m,则BB'的长为( )
A.1 m B.2 m C.3 m D.4 m
9.(教材P4变式题)如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E.
(1)求△ABC的面积;
(2)求DE的值.
10.(2022独家原创)学完勾股定理后,活动课上,老师让学生们求一个△ABC的面积,小明测量出AB=17 cm,BC=9 cm,AC=10 cm,请你帮小明求出△ABC的面积.
11.(2022贵州六盘水月考)如图,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,点P从点A出发,以每秒1 cm的速度向点C运动,连接PB,设运动时间为t秒(t>0).
(1)当△PBC的面积为△ABC面积的一半时,求t的值;
(2)当t为何值时,AP=PB
能力提升全练
12.(2021山西中考,8,)在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
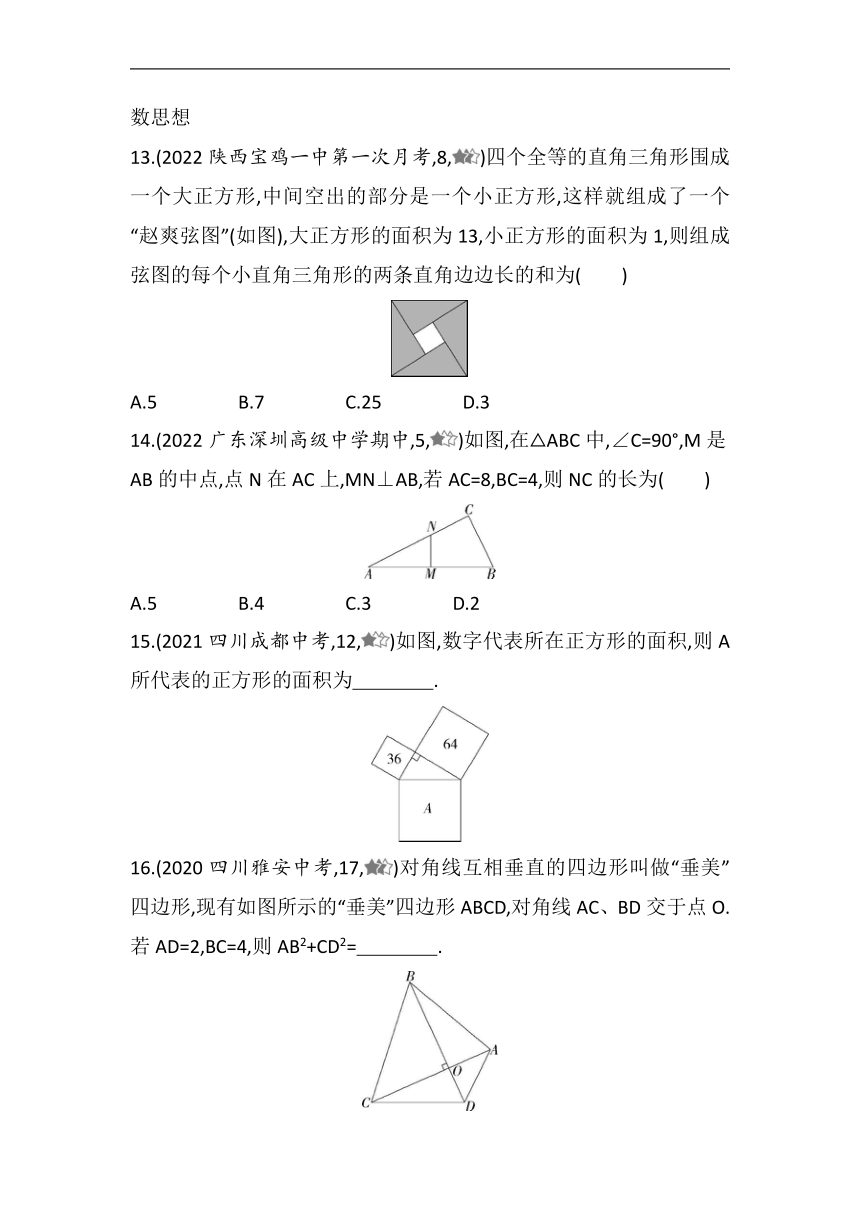
13.(2022陕西宝鸡一中第一次月考,8,)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( )
A.5 B.7 C.25 D.3
14.(2022广东深圳高级中学期中,5,)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
15.(2021四川成都中考,12,)如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 .
16.(2020四川雅安中考,17,)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2= .
17.(2022甘肃兰州教育局第四片区期中,25,)在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁 请通过计算进行说明.
素养探究全练
18.[直观想象](2020湖北随州中考节选)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图4、图5、图6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,则这三个图形中面积关系满足S1+S2=S3的有 个.
②如图7所示,分别以直角三角形的三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明.
答案全解全析
基础过关全练
1.D 勾股定理只应用在直角三角形里,并且要指出明确的直角,故选项A、B中的说法错误;选项C中的斜边长为a,得出的表达式应为b2+c2=a2,故选项C中的说法错误;只有选项D中的说法正确.故选D.
2.C 由勾股定理得AC2+BC2=AB2,∴S3+S2=S1.
∵S1+S2+S3=12,∴2S1=12,∴S1=6,故选C.
3.A 在Rt△ABC中,AB2=AC2+BC2=42=16,
S1=π=·AC2,S2=π=·BC2,
∴S1+S2=(AC2+BC2)=×16=2π.故选A.
4.169
解析 Rt△ABC中,∠C=90°,
∴AB2=AC2+BC2=52+122=169,
∴正方形ABDE的面积=AB2=169.
5.解析 (1)∵大正方形的面积表示为S=c2,又可表示为S=4×ab+(b-a)2,
∴4×ab+(b-a)2=c2,∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.故填4×ab+(b-a)2;4×ab+(b-a)2;a2+b2=c2.
(2)证明:大正方形的面积=ab×4+c2=(a+b)(a+b),整理,得2ab+c2=a2+b2+2ab,即a2+b2=c2.
(3)证明:如图,过A作AF⊥AB,过E作EF⊥AF于F,延长FE交BC的延长线于D,则四边形ABDF是长方形.
∵∠ACE=90°,∴∠ACB+∠ECD=90°.
∵∠ABC=90°,
∴∠ACB+∠BAC=90°,
∴∠BAC=∠ECD,
∵∠B=∠D=90°,∴△ABC≌△CDE(AAS),
∴CD=AB=b,DE=BC=a,
∴S长方形ABDF=b(a+b)=2×ab+c2+(b-a)(a+b),
∴a2+b2=c2.
6.A ∵△DAB的面积=DA·BC,∴×10BC=40,解得BC=8,
Rt△DBC中,∠C=90°,DB=10,CB=8,
∴CD2=BD2-BC2=102-82=36,∴CD=6,故选A.
7.C 如图1,此时筷子露在杯子外面的长度最大,为24-12=12 cm.
如图2,此时筷子露在杯子外面的长度最短,AB2=BC2+AC2=52+122=169,
∴AB=13 cm,
此时h=24-13=11.
故h的取值范围是11≤h≤12.故选C.
8.B 在Rt△ABC中,AC=10 m,BC=6 m,
∴AB2=AC2-BC2=100-36=64,
∴AB=8 m,
在Rt△AC'B'中,AC'=10 m,B'C'=8 m,
∴AB'2=AC'2-B'C'2=36,∴AB'=6 m,
∴BB'=AB-AB'=8-6=2(m).
故选B.
9.解析 (1)如图,连接AD,
∵在△ABC中,AB=AC=13,BC=10,点D为BC的中点,
∴AD⊥BC,BD=BC=5,
∴AD2=AB2-BD2=132-52=144,
∴AD=12,
∴S△ABC=BC·AD=×10×12=60.
(2)∵DE⊥AB,
∴S△ABD=BD·AD=AB·ED,
∴ED===.
10.解析 如图,作AD⊥BC,交BC的延长线于D,
设CD=x cm,则BD=(x+9)cm,
∵∠D=90°,
∴AD2=AB2-BD2,
又∵AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
∴172-(x+9)2=102-x2,
解得x=6,
∴CD=6 cm,∴AD2=102-62=64,
∴AD=8 cm,
∴S△ABC=×9×8=36 cm2.
11.解析 (1)由题意得AP=t cm,
当BP是△ABC的中线时,△PBC的面积为△ABC面积的一半,
∴t=AC=8.
答:当△PBC的面积为△ABC面积的一半时,t=8.
(2)易知AP=t cm,PC=(16-t)cm,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,
∴BC2=AB2-AC2=202-162=144,
∴BC=12 cm,
在Rt△PBC中,PB2=PC2+BC2=(16-t)2+122,
当AP=PB时,t2=(16-t)2+122,
解得t=,
∴当t=时,AP=PB.
能力提升全练
12.C 由图形关系转化为数量关系,体现数形结合思想,故选C.
13.A 设小直角三角形的两条直角边的边长分别为a、b,
由题意可得ab×4=13-1,a2+b2=13,
∴ab=6,
∴(a+b)2=a2+2ab+b2=(a2+b2)+2ab=13+2×6=13+12=25,
∴a+b=5或a+b=-5(舍去),
故选A.
14.C 如图所示,连接BN,
∵M为AB的中点,MN⊥AB,∴AN=BN,
设NC=x,则AN=BN=AC-NC=8-x,
∵∠C=90°,∴CN2+BC2=BN2,
∴x2+42=(8-x)2,
解得x=3,
∴NC=3,
故选C.
15.100
解析 由题意可知,直角三角形中,一条直角边的平方=36,另一条直角边的平方=64,
则斜边的平方=36+64=100.故答案为100.
16.20
解析 ∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得AB2+CD2=AO2+BO2+CO2+DO2,
AD2+BC2=AO2+DO2+BO2+CO2,
∴AB2+CD2=AD2+BC2.
∵AD=2,BC=4,
∴AB2+CD2=22+42=20.
故答案为20.
17.解析 如图,过C作CD⊥AB于D,
∵BC=400米,AC=300米,∠ACB=90°,
∴AB=500米,
∵AB·CD=BC·AC,
∴CD=240米,
∵240米<250米,故有危险,
因此在进行爆破时,公路AB段需要暂时封锁.
素养探究全练
18.解析 (1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.
(或者:在直角三角形中,两条直角边的平方和等于斜边的平方)
②证明:在题图1中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即c2=ab×4+(b-a)2,
化简得a2+b2=c2.
在题图2中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即(a+b)2=c2+ab×4,
化简得a2+b2=c2.
在题图3中,梯形的面积等于三个直角三角形的面积的和,
即(a+b)(a+b)=ab×2+c2,
化简得a2+b2=c2.
(2)①3.
②S1+S2=S3.
证明:∵S1+S2=π+π+S3-π,
∴S1+S2=π(a2+b2-c2)+S3,
∵a2+b2=c2.
∴S1+S2=S3.
课堂提升训练
第一章 勾股定理
1 探索勾股定理
基础过关全练
知识点1 勾股定理
1.(2022山东枣庄四中月考)下列说法正确的是( )
A.若a、b、c是△ABC的三边长,则a2+b2=c2
B.若a、b、c是Rt△ABC的三边长,则a2+b2=c2
C.若a、b、c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a、b、c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
2.(2021四川资阳期末)如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( )
A.4 B.5 C.6 D.7
3.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π C.8π D.16π
4.如图,Rt△ABC中,∠C=90°,AC=5,BC=12,则正方形ABDE的面积是 .
知识点2 验证勾股定理
5.(1)我国著名的数学家赵爽早在公元3世纪就把一个长方形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图①),这个正方形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中,两直角边a、b与斜边c满足关系式:a2+b2=c2,称为勾股定理.
证明:∵大正方形的面积表示为S=c2,
又可表示为S= ,
∴ =c2, ∴ ,
即直角三角形两直角边的平方和等于斜边的平方;
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②),也能验证这个结论,请你帮助小明完成验证的过程;
(3)如图③所示,∠ABC=∠ACE=90°,请你添加适当的辅助线证明结论a2+b2=c2.
知识点3 勾股定理的简单应用
6.(2022辽宁凌海期中)如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=10,如果△DAB的面积为40,那么DC的长为( )
A.6 B.7 C.8 D.9
7.(2021四川乐山犍为期末)如图,将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中,设筷子露在杯子外面的长度是h cm,则h的取值范围是( )
A.5≤h≤12 B.12≤h≤19
C.11≤h≤12 D.12≤h≤13
8.(2022山东济南济阳期中)如图,已知钓鱼竿AC的长为10 m,露在水面上的鱼线BC长为6 m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8 m,则BB'的长为( )
A.1 m B.2 m C.3 m D.4 m
9.(教材P4变式题)如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E.
(1)求△ABC的面积;
(2)求DE的值.
10.(2022独家原创)学完勾股定理后,活动课上,老师让学生们求一个△ABC的面积,小明测量出AB=17 cm,BC=9 cm,AC=10 cm,请你帮小明求出△ABC的面积.
11.(2022贵州六盘水月考)如图,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,点P从点A出发,以每秒1 cm的速度向点C运动,连接PB,设运动时间为t秒(t>0).
(1)当△PBC的面积为△ABC面积的一半时,求t的值;
(2)当t为何值时,AP=PB
能力提升全练
12.(2021山西中考,8,)在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
13.(2022陕西宝鸡一中第一次月考,8,)四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( )
A.5 B.7 C.25 D.3
14.(2022广东深圳高级中学期中,5,)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
15.(2021四川成都中考,12,)如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 .
16.(2020四川雅安中考,17,)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2= .
17.(2022甘肃兰州教育局第四片区期中,25,)在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁 请通过计算进行说明.
素养探究全练
18.[直观想象](2020湖北随州中考节选)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图4、图5、图6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,则这三个图形中面积关系满足S1+S2=S3的有 个.
②如图7所示,分别以直角三角形的三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明.
答案全解全析
基础过关全练
1.D 勾股定理只应用在直角三角形里,并且要指出明确的直角,故选项A、B中的说法错误;选项C中的斜边长为a,得出的表达式应为b2+c2=a2,故选项C中的说法错误;只有选项D中的说法正确.故选D.
2.C 由勾股定理得AC2+BC2=AB2,∴S3+S2=S1.
∵S1+S2+S3=12,∴2S1=12,∴S1=6,故选C.
3.A 在Rt△ABC中,AB2=AC2+BC2=42=16,
S1=π=·AC2,S2=π=·BC2,
∴S1+S2=(AC2+BC2)=×16=2π.故选A.
4.169
解析 Rt△ABC中,∠C=90°,
∴AB2=AC2+BC2=52+122=169,
∴正方形ABDE的面积=AB2=169.
5.解析 (1)∵大正方形的面积表示为S=c2,又可表示为S=4×ab+(b-a)2,
∴4×ab+(b-a)2=c2,∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.故填4×ab+(b-a)2;4×ab+(b-a)2;a2+b2=c2.
(2)证明:大正方形的面积=ab×4+c2=(a+b)(a+b),整理,得2ab+c2=a2+b2+2ab,即a2+b2=c2.
(3)证明:如图,过A作AF⊥AB,过E作EF⊥AF于F,延长FE交BC的延长线于D,则四边形ABDF是长方形.
∵∠ACE=90°,∴∠ACB+∠ECD=90°.
∵∠ABC=90°,
∴∠ACB+∠BAC=90°,
∴∠BAC=∠ECD,
∵∠B=∠D=90°,∴△ABC≌△CDE(AAS),
∴CD=AB=b,DE=BC=a,
∴S长方形ABDF=b(a+b)=2×ab+c2+(b-a)(a+b),
∴a2+b2=c2.
6.A ∵△DAB的面积=DA·BC,∴×10BC=40,解得BC=8,
Rt△DBC中,∠C=90°,DB=10,CB=8,
∴CD2=BD2-BC2=102-82=36,∴CD=6,故选A.
7.C 如图1,此时筷子露在杯子外面的长度最大,为24-12=12 cm.
如图2,此时筷子露在杯子外面的长度最短,AB2=BC2+AC2=52+122=169,
∴AB=13 cm,
此时h=24-13=11.
故h的取值范围是11≤h≤12.故选C.
8.B 在Rt△ABC中,AC=10 m,BC=6 m,
∴AB2=AC2-BC2=100-36=64,
∴AB=8 m,
在Rt△AC'B'中,AC'=10 m,B'C'=8 m,
∴AB'2=AC'2-B'C'2=36,∴AB'=6 m,
∴BB'=AB-AB'=8-6=2(m).
故选B.
9.解析 (1)如图,连接AD,
∵在△ABC中,AB=AC=13,BC=10,点D为BC的中点,
∴AD⊥BC,BD=BC=5,
∴AD2=AB2-BD2=132-52=144,
∴AD=12,
∴S△ABC=BC·AD=×10×12=60.
(2)∵DE⊥AB,
∴S△ABD=BD·AD=AB·ED,
∴ED===.
10.解析 如图,作AD⊥BC,交BC的延长线于D,
设CD=x cm,则BD=(x+9)cm,
∵∠D=90°,
∴AD2=AB2-BD2,
又∵AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
∴172-(x+9)2=102-x2,
解得x=6,
∴CD=6 cm,∴AD2=102-62=64,
∴AD=8 cm,
∴S△ABC=×9×8=36 cm2.
11.解析 (1)由题意得AP=t cm,
当BP是△ABC的中线时,△PBC的面积为△ABC面积的一半,
∴t=AC=8.
答:当△PBC的面积为△ABC面积的一半时,t=8.
(2)易知AP=t cm,PC=(16-t)cm,在Rt△ABC中,∠ACB=90°,AB=20 cm,AC=16 cm,
∴BC2=AB2-AC2=202-162=144,
∴BC=12 cm,
在Rt△PBC中,PB2=PC2+BC2=(16-t)2+122,
当AP=PB时,t2=(16-t)2+122,
解得t=,
∴当t=时,AP=PB.
能力提升全练
12.C 由图形关系转化为数量关系,体现数形结合思想,故选C.
13.A 设小直角三角形的两条直角边的边长分别为a、b,
由题意可得ab×4=13-1,a2+b2=13,
∴ab=6,
∴(a+b)2=a2+2ab+b2=(a2+b2)+2ab=13+2×6=13+12=25,
∴a+b=5或a+b=-5(舍去),
故选A.
14.C 如图所示,连接BN,
∵M为AB的中点,MN⊥AB,∴AN=BN,
设NC=x,则AN=BN=AC-NC=8-x,
∵∠C=90°,∴CN2+BC2=BN2,
∴x2+42=(8-x)2,
解得x=3,
∴NC=3,
故选C.
15.100
解析 由题意可知,直角三角形中,一条直角边的平方=36,另一条直角边的平方=64,
则斜边的平方=36+64=100.故答案为100.
16.20
解析 ∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得AB2+CD2=AO2+BO2+CO2+DO2,
AD2+BC2=AO2+DO2+BO2+CO2,
∴AB2+CD2=AD2+BC2.
∵AD=2,BC=4,
∴AB2+CD2=22+42=20.
故答案为20.
17.解析 如图,过C作CD⊥AB于D,
∵BC=400米,AC=300米,∠ACB=90°,
∴AB=500米,
∵AB·CD=BC·AC,
∴CD=240米,
∵240米<250米,故有危险,
因此在进行爆破时,公路AB段需要暂时封锁.
素养探究全练
18.解析 (1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.
(或者:在直角三角形中,两条直角边的平方和等于斜边的平方)
②证明:在题图1中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即c2=ab×4+(b-a)2,
化简得a2+b2=c2.
在题图2中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即(a+b)2=c2+ab×4,
化简得a2+b2=c2.
在题图3中,梯形的面积等于三个直角三角形的面积的和,
即(a+b)(a+b)=ab×2+c2,
化简得a2+b2=c2.
(2)①3.
②S1+S2=S3.
证明:∵S1+S2=π+π+S3-π,
∴S1+S2=π(a2+b2-c2)+S3,
∵a2+b2=c2.
∴S1+S2=S3.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
