2022届数学高考冲刺思维锻炼型解答大题易错汇编(含解析)
文档属性
| 名称 | 2022届数学高考冲刺思维锻炼型解答大题易错汇编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 16:35:13 | ||
图片预览




文档简介
高三模拟卷解答大题精编(学生版)
1:(2022浙江三校模拟)
已知是抛物线上的点,,.直线与抛物线在第四象限交于点、,且.
(1)若,求抛物线的焦点坐标;(2)求的取值范围.
2:(2021年11月稽阳联考)
已知点,直线与直线的斜率之积为.
(I)求点的轨迹的方程;
(II)点是轨迹上的动点,直线,斜率分别为满足,求中点横坐标的取值范围.
3:(21年4月湖丽衢)
已知三棱柱,是正三角形,四边形是菱形且°,
是的中点,.
(1)证明:;(2)求直线与平面所成角的正弦值.
4:(名校交流仿真卷一)
5:(名校交流仿真卷一)
6:(2022浙江三校模拟)
已知为等比数列,为等差数列,为递增数列,满足:,,(为常数,).
(I)求实数的取值范围;
(II)设,证明:,.
7:(2021年4月金华十校联考)
已知数列的前项和为,,数列满足:当成等比数列时,公比为,当成等差数列时,公差也为
(1)求与;
(2)证明:.
8:(2022浙江三校模拟)
设函数,其中, 自然对数的底.
(I)求的导函数;
(II)当时,证明存在正实数使得恒成立,并求的最小值.
9:(2022届杭州周边地区高三期中)
已知,直线为曲线在处的切线,直线与曲线相交于点 且.
(II) ① 求的取值范围; ②证明:.
10:(镇海中学2021 学年第一学期期末考试)
已知函数,,.(3)当时,若函数有两个不同的极值点.证明:.
11:(2021年10月浙江省五校联考)
已知函数.
(1)若,求证:当时,;
(2)讨论方程的根的个数.
12:(2021年11月宁波高考模拟考第22题)
已知函数.
(Ⅰ)当时,求函数的单调区间;
(Ⅱ)若函数有两个不同零点,
(ⅰ)求实数的取值范围; (ⅱ)求证:.
13:(2022高三下期初协作体)
已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)设函数,
(i)若有且只有一个零点,求实数的取值范围;
(ii)记函数,若关于的方程有个根,从小到大依次为 ,求证:;.
14:(镇海中学周测)
数列满足,.
(1)求数列的通项公式及前项和;
(2)令,(),记数列的前项和,
证明:.
高三模拟卷解答大题精编(教师版)
1:(2022浙江三校模拟)
已知是抛物线上的点,,.直线与抛物线在第四象限交于点、,且.
(1)若,求抛物线的焦点坐标;(2)求的取值范围.
两点距离公式 P到抛物线下半支上一点的距离不单调即可
【类似】【2016浙江19】设椭圆
(Ⅰ)求直线被椭圆截得到的弦长(用a,k表示)
(Ⅱ)若任意以点为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
2:(2021年11月稽阳联考)
已知点,直线与直线的斜率之积为.
(I)求点的轨迹的方程;
(II)点是轨迹上的动点,直线,斜率分别为满足,求中点横坐标的取值范围.
(Ⅰ)解析:设,因为直线与直线的斜率之积为,所以
,可得.
所以点的轨迹的方程为(除去点)★
(II)解析1:设直线的方程为,则
由消去得:
由消去得:
由(I)知: 所以,
又,所以,解得,此时方程有两个不同的实根,符合题意.
.
解析2:设直线为,由消得,解得
设直线为,则由消得:,解得
所以
令,则当时,
,, 当时,,所以
【对勾型整体换元】
【类似】已知,则的最大值为 .
【齐次化消元】常规做法两个分式均上下同除。如果直接假设后得到原式,此时要注意分子次数为次,分母为次,中间次数均为,故可以通过上下同除来进行的整体换元.
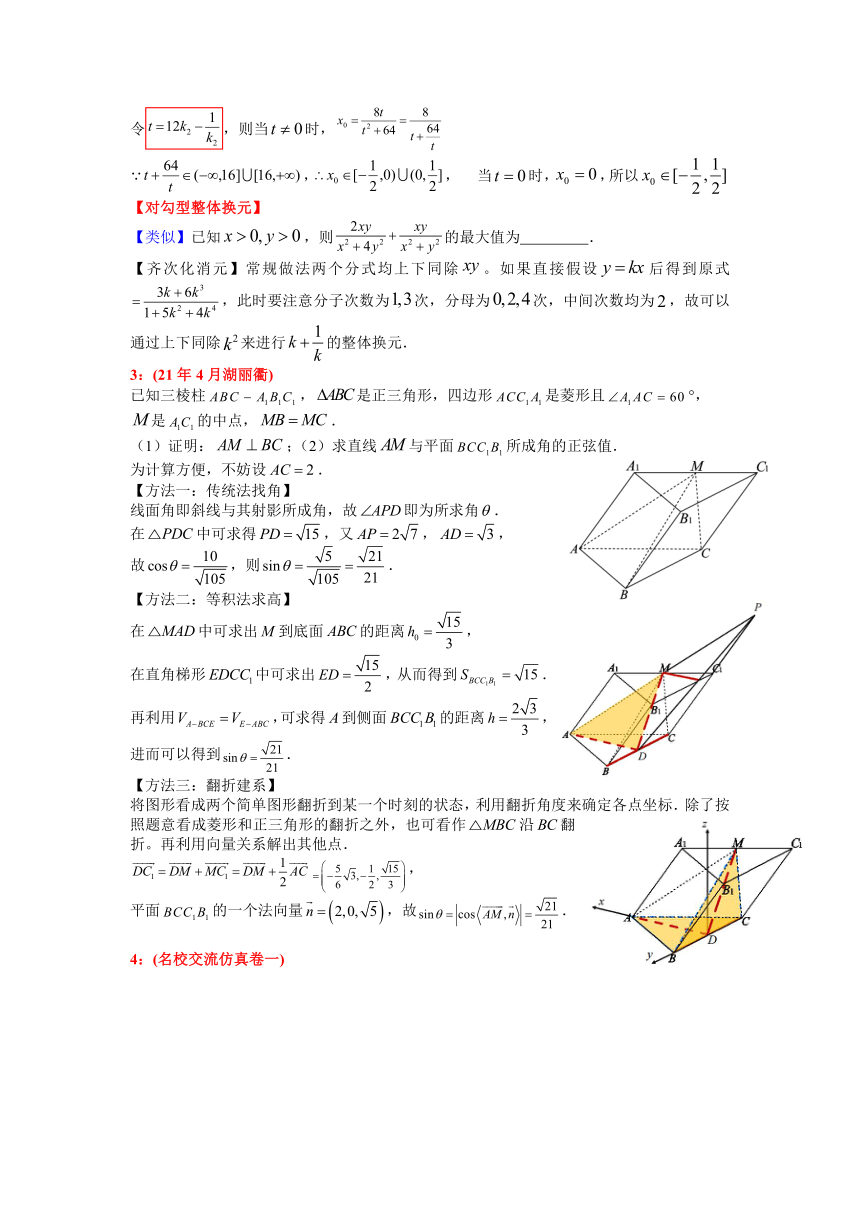
3:(21年4月湖丽衢)
已知三棱柱,是正三角形,四边形是菱形且°,
是的中点,.
(1)证明:;(2)求直线与平面所成角的正弦值.
为计算方便,不妨设.
【方法一:传统法找角】
线面角即斜线与其射影所成角,故即为所求角.
在中可求得,又,,
故,则.
【方法二:等积法求高】
在中可求出到底面的距离,
在直角梯形中可求出,从而得到.
再利用,可求得到侧面的距离,
进而可以得到.
【方法三:翻折建系】
将图形看成两个简单图形翻折到某一个时刻的状态,利用翻折角度来确定各点坐标.除了按照题意看成菱形和正三角形的翻折之外,也可看作沿翻折。再利用向量关系解出其他点.
,
平面的一个法向量,故.
4:(名校交流仿真卷一)
5:(名校交流仿真卷一)
6:(2022浙江三校模拟)
已知为等比数列,为等差数列,为递增数列,满足:,,(为常数,).
(I)求实数的取值范围;
(II)设,证明:,.
(Ⅰ)解析:由题意得.
因为为等比数列,为等差数列,
所以,
所以,
由为递增数列,则恒成立,所以
(II)解析:
(1)当时,,不等式成立;
(2)当时,
(注:第二个不等号用到了糖水不等式,此处也可用分析法证明)
则,所以
由(I)得:,所以,
因为,
(注:①此处可以用待定系数法,如下操作:,然后通分左右对比确定系数;②的前项和也可用错位相减法.)
所以
.
综上,,.
7:(2021年4月金华十校联考)
已知数列的前项和为,,数列满足:当成等比数列时,公比为,当成等差数列时,公差也为
(1)求与;
(2)证明:.
(1)解析:由题可知:
(2)解析:当时,,,
则,即
当时,,,
则,即
则
当时,则,即
当时,,即
综上:
8:(2022浙江三校模拟)
设函数,其中, 自然对数的底.
(I)求的导函数;
(II)当时,证明存在正实数使得恒成立,并求的最小值.
【解析】(I)由得,
(II)设
先证:当时,对任意,存在实数,使得.
当时,令,此时,显然存在,使.
当时,令,此时,显然存在,使.
因此,若恒成立,则,即
再求的最小值.
(i)当时,等价于.
记,则,
记,则.
所以在上递增.又,若恒成立,
则,验证得等号可以成立.
(ii)当时,等价于.由(i)得,,
所以, 所以在上递减,有恒成立.
从而,的最小值为1.
综上,存在正实数使得恒成立,且的最小值为3, 此时.
几何背景:拐点(凹凸性改变)
【类似】T2 (II)①
【类似】【2018年浙江高考22】已知函数f(x)= lnx.
(Ⅰ)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8 8ln2;
(Ⅱ)若a≤3 4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
(Ⅱ)令m=,n=,则f(m)–km–a>|a|+k–k–a≥0,
f(n)–kn–a<≤<0,所以存在x0∈(m,n)使f(x0)=kx0+a,
所以对于任意的a∈R及k∈(0,+∞),直线y=kx+a与曲线y=f(x)有公共点.
由f(x)=kx+a得.
设h(x)=,则h′(x)=,其中g(x)=.
由(Ⅰ)可知g(x)≥g(16),又a≤3–4ln2,
故–g(x)–1+a≤–g(16)–1+a=–3+4ln2+a≤0,
所以h′(x)≤0,函数h(x)在(0,+∞)上单调递减,方程f(x)–kx–a=0至多1个实根.
综上,当a≤3–4ln2时,对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
9:(2022届杭州周边地区高三期中)
已知,直线为曲线在处的切线,直线与曲线相交于点 且.
(II) ① 求的取值范围; ②证明:.
【解析】(II) ①在处的切线为,
令,, 转化为在上有零点,求取值范围.
则,则在减增,
若时,, 所以,
则在增且,所以在上无零点,舍去.
若,因为, 所以时,
又当时,,所以存在,使.
则在增,减,而时,,所以在存在零点.
综上:对的取值范围是.
②因为是上的点,所以
所以
.
10:(镇海中学2021 学年第一学期期末考试)
已知函数,,.(3)当时,若函数有两个不同的极值点.证明:.
【解析】渐近线放缩
(3)原问题等价于证明:.
记,则的两个根为.
则.令,
则.所以在.
所以,即.所以.
所以,即.
所以.下证:.
由在,只需证:.
.显然成立.所以.
所以.
【拓展问题】
(1)(注:);
(2);
(3);
(4);
(5).
11:(2021年10月浙江省五校联考)
已知函数.
(1)若,求证:当时,;
(2)讨论方程的根的个数.
(2)【解析】(隐零点)
令,,,
在单调递减,在单调递增,
若,则有,故在上单调递增,
因为,,故在上有唯一零点,;
若,则,,,
,故存在,,使得,
有,有,有,
故为极大值,为极小值,
若,
因为,故,
故结合和可知此时有唯一零点;
若,
由(1)可知,故,故结合在上单调递减可知(),
又因为在上单调递减,故(),
故结合和可知此时有三个零点;
综上,当时方程仅有1个根,当方程有3个根.
【改进:换元后不会出现指数,对数方便计算】
12:(2021年11月宁波高考模拟考第22题)
已知函数.
(Ⅰ)当时,求函数的单调区间;
(Ⅱ)若函数有两个不同零点,
(ⅰ)求实数的取值范围; (ⅱ)求证:.
【解析】
(ⅱ)注意到,,要证,只需证.
由(ⅰ)知,,故有,即. 下面证明:.
设,
有,
所以函数在上单调递增,所以,所以,
故有.又,且在上单调递减,所以,即得.
因此,,结论得证.
13:(2022高三下期初协作体)
已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)设函数,
(i)若有且只有一个零点,求实数的取值范围;
(ii)记函数,若关于的方程有个根,从小到大依次为 ,求证:;.
【解析】
(Ⅰ)令, ,
, ……2分
在定义域上单调递减,所以 为的极大值点, …… 4分
所以在上单调递增,单调递减. ……5分
(或者求出的单调区间,再利用对称性得的单调区间)
(Ⅱ)(i),
因为 ……7分
,当时取等号. ……9分
所以当时,,单调递减,又,符合要求.
当时,由的对称性,只需考虑
,由 得
又,所以在上有零点,又..,
与有且只有一个零点矛盾.
综上:. ……11分
(ii)由的对称性,关于轴对称,
有4个根,由(i)中分析可知,
,所以,
不妨考虑时, 此时,考虑在处的切线,
记,由(i)得,
所以,即在上恒成立,
,
推出,所以,所以 ……13分
又时,
推出,并由对称性,.……15分
14:(镇海中学周测)
数列满足,.
(1)求数列的通项公式及前项和;
(2)令,(),记数列的前项和,
证明:.
【解析】
(1)解:,当时,,
两式相减,得,所以(),又也满足,故().所以.
(2)证明:当时,,,不等式成立;
当时
.
要证,只需证,即证,
只需证,只需证,
设,则,,只需(),①
设,则,所以在上递减,,即不等式①成立.综上,数列的前项和满足.
1:(2022浙江三校模拟)
已知是抛物线上的点,,.直线与抛物线在第四象限交于点、,且.
(1)若,求抛物线的焦点坐标;(2)求的取值范围.
2:(2021年11月稽阳联考)
已知点,直线与直线的斜率之积为.
(I)求点的轨迹的方程;
(II)点是轨迹上的动点,直线,斜率分别为满足,求中点横坐标的取值范围.
3:(21年4月湖丽衢)
已知三棱柱,是正三角形,四边形是菱形且°,
是的中点,.
(1)证明:;(2)求直线与平面所成角的正弦值.
4:(名校交流仿真卷一)
5:(名校交流仿真卷一)
6:(2022浙江三校模拟)
已知为等比数列,为等差数列,为递增数列,满足:,,(为常数,).
(I)求实数的取值范围;
(II)设,证明:,.
7:(2021年4月金华十校联考)
已知数列的前项和为,,数列满足:当成等比数列时,公比为,当成等差数列时,公差也为
(1)求与;
(2)证明:.
8:(2022浙江三校模拟)
设函数,其中, 自然对数的底.
(I)求的导函数;
(II)当时,证明存在正实数使得恒成立,并求的最小值.
9:(2022届杭州周边地区高三期中)
已知,直线为曲线在处的切线,直线与曲线相交于点 且.
(II) ① 求的取值范围; ②证明:.
10:(镇海中学2021 学年第一学期期末考试)
已知函数,,.(3)当时,若函数有两个不同的极值点.证明:.
11:(2021年10月浙江省五校联考)
已知函数.
(1)若,求证:当时,;
(2)讨论方程的根的个数.
12:(2021年11月宁波高考模拟考第22题)
已知函数.
(Ⅰ)当时,求函数的单调区间;
(Ⅱ)若函数有两个不同零点,
(ⅰ)求实数的取值范围; (ⅱ)求证:.
13:(2022高三下期初协作体)
已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)设函数,
(i)若有且只有一个零点,求实数的取值范围;
(ii)记函数,若关于的方程有个根,从小到大依次为 ,求证:;.
14:(镇海中学周测)
数列满足,.
(1)求数列的通项公式及前项和;
(2)令,(),记数列的前项和,
证明:.
高三模拟卷解答大题精编(教师版)
1:(2022浙江三校模拟)
已知是抛物线上的点,,.直线与抛物线在第四象限交于点、,且.
(1)若,求抛物线的焦点坐标;(2)求的取值范围.
两点距离公式 P到抛物线下半支上一点的距离不单调即可
【类似】【2016浙江19】设椭圆
(Ⅰ)求直线被椭圆截得到的弦长(用a,k表示)
(Ⅱ)若任意以点为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
2:(2021年11月稽阳联考)
已知点,直线与直线的斜率之积为.
(I)求点的轨迹的方程;
(II)点是轨迹上的动点,直线,斜率分别为满足,求中点横坐标的取值范围.
(Ⅰ)解析:设,因为直线与直线的斜率之积为,所以
,可得.
所以点的轨迹的方程为(除去点)★
(II)解析1:设直线的方程为,则
由消去得:
由消去得:
由(I)知: 所以,
又,所以,解得,此时方程有两个不同的实根,符合题意.
.
解析2:设直线为,由消得,解得
设直线为,则由消得:,解得
所以
令,则当时,
,, 当时,,所以
【对勾型整体换元】
【类似】已知,则的最大值为 .
【齐次化消元】常规做法两个分式均上下同除。如果直接假设后得到原式,此时要注意分子次数为次,分母为次,中间次数均为,故可以通过上下同除来进行的整体换元.
3:(21年4月湖丽衢)
已知三棱柱,是正三角形,四边形是菱形且°,
是的中点,.
(1)证明:;(2)求直线与平面所成角的正弦值.
为计算方便,不妨设.
【方法一:传统法找角】
线面角即斜线与其射影所成角,故即为所求角.
在中可求得,又,,
故,则.
【方法二:等积法求高】
在中可求出到底面的距离,
在直角梯形中可求出,从而得到.
再利用,可求得到侧面的距离,
进而可以得到.
【方法三:翻折建系】
将图形看成两个简单图形翻折到某一个时刻的状态,利用翻折角度来确定各点坐标.除了按照题意看成菱形和正三角形的翻折之外,也可看作沿翻折。再利用向量关系解出其他点.
,
平面的一个法向量,故.
4:(名校交流仿真卷一)
5:(名校交流仿真卷一)
6:(2022浙江三校模拟)
已知为等比数列,为等差数列,为递增数列,满足:,,(为常数,).
(I)求实数的取值范围;
(II)设,证明:,.
(Ⅰ)解析:由题意得.
因为为等比数列,为等差数列,
所以,
所以,
由为递增数列,则恒成立,所以
(II)解析:
(1)当时,,不等式成立;
(2)当时,
(注:第二个不等号用到了糖水不等式,此处也可用分析法证明)
则,所以
由(I)得:,所以,
因为,
(注:①此处可以用待定系数法,如下操作:,然后通分左右对比确定系数;②的前项和也可用错位相减法.)
所以
.
综上,,.
7:(2021年4月金华十校联考)
已知数列的前项和为,,数列满足:当成等比数列时,公比为,当成等差数列时,公差也为
(1)求与;
(2)证明:.
(1)解析:由题可知:
(2)解析:当时,,,
则,即
当时,,,
则,即
则
当时,则,即
当时,,即
综上:
8:(2022浙江三校模拟)
设函数,其中, 自然对数的底.
(I)求的导函数;
(II)当时,证明存在正实数使得恒成立,并求的最小值.
【解析】(I)由得,
(II)设
先证:当时,对任意,存在实数,使得.
当时,令,此时,显然存在,使.
当时,令,此时,显然存在,使.
因此,若恒成立,则,即
再求的最小值.
(i)当时,等价于.
记,则,
记,则.
所以在上递增.又,若恒成立,
则,验证得等号可以成立.
(ii)当时,等价于.由(i)得,,
所以, 所以在上递减,有恒成立.
从而,的最小值为1.
综上,存在正实数使得恒成立,且的最小值为3, 此时.
几何背景:拐点(凹凸性改变)
【类似】T2 (II)①
【类似】【2018年浙江高考22】已知函数f(x)= lnx.
(Ⅰ)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8 8ln2;
(Ⅱ)若a≤3 4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
(Ⅱ)令m=,n=,则f(m)–km–a>|a|+k–k–a≥0,
f(n)–kn–a<≤<0,所以存在x0∈(m,n)使f(x0)=kx0+a,
所以对于任意的a∈R及k∈(0,+∞),直线y=kx+a与曲线y=f(x)有公共点.
由f(x)=kx+a得.
设h(x)=,则h′(x)=,其中g(x)=.
由(Ⅰ)可知g(x)≥g(16),又a≤3–4ln2,
故–g(x)–1+a≤–g(16)–1+a=–3+4ln2+a≤0,
所以h′(x)≤0,函数h(x)在(0,+∞)上单调递减,方程f(x)–kx–a=0至多1个实根.
综上,当a≤3–4ln2时,对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
9:(2022届杭州周边地区高三期中)
已知,直线为曲线在处的切线,直线与曲线相交于点 且.
(II) ① 求的取值范围; ②证明:.
【解析】(II) ①在处的切线为,
令,, 转化为在上有零点,求取值范围.
则,则在减增,
若时,, 所以,
则在增且,所以在上无零点,舍去.
若,因为, 所以时,
又当时,,所以存在,使.
则在增,减,而时,,所以在存在零点.
综上:对的取值范围是.
②因为是上的点,所以
所以
.
10:(镇海中学2021 学年第一学期期末考试)
已知函数,,.(3)当时,若函数有两个不同的极值点.证明:.
【解析】渐近线放缩
(3)原问题等价于证明:.
记,则的两个根为.
则.令,
则.所以在.
所以,即.所以.
所以,即.
所以.下证:.
由在,只需证:.
.显然成立.所以.
所以.
【拓展问题】
(1)(注:);
(2);
(3);
(4);
(5).
11:(2021年10月浙江省五校联考)
已知函数.
(1)若,求证:当时,;
(2)讨论方程的根的个数.
(2)【解析】(隐零点)
令,,,
在单调递减,在单调递增,
若,则有,故在上单调递增,
因为,,故在上有唯一零点,;
若,则,,,
,故存在,,使得,
有,有,有,
故为极大值,为极小值,
若,
因为,故,
故结合和可知此时有唯一零点;
若,
由(1)可知,故,故结合在上单调递减可知(),
又因为在上单调递减,故(),
故结合和可知此时有三个零点;
综上,当时方程仅有1个根,当方程有3个根.
【改进:换元后不会出现指数,对数方便计算】
12:(2021年11月宁波高考模拟考第22题)
已知函数.
(Ⅰ)当时,求函数的单调区间;
(Ⅱ)若函数有两个不同零点,
(ⅰ)求实数的取值范围; (ⅱ)求证:.
【解析】
(ⅱ)注意到,,要证,只需证.
由(ⅰ)知,,故有,即. 下面证明:.
设,
有,
所以函数在上单调递增,所以,所以,
故有.又,且在上单调递减,所以,即得.
因此,,结论得证.
13:(2022高三下期初协作体)
已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)设函数,
(i)若有且只有一个零点,求实数的取值范围;
(ii)记函数,若关于的方程有个根,从小到大依次为 ,求证:;.
【解析】
(Ⅰ)令, ,
, ……2分
在定义域上单调递减,所以 为的极大值点, …… 4分
所以在上单调递增,单调递减. ……5分
(或者求出的单调区间,再利用对称性得的单调区间)
(Ⅱ)(i),
因为 ……7分
,当时取等号. ……9分
所以当时,,单调递减,又,符合要求.
当时,由的对称性,只需考虑
,由 得
又,所以在上有零点,又..,
与有且只有一个零点矛盾.
综上:. ……11分
(ii)由的对称性,关于轴对称,
有4个根,由(i)中分析可知,
,所以,
不妨考虑时, 此时,考虑在处的切线,
记,由(i)得,
所以,即在上恒成立,
,
推出,所以,所以 ……13分
又时,
推出,并由对称性,.……15分
14:(镇海中学周测)
数列满足,.
(1)求数列的通项公式及前项和;
(2)令,(),记数列的前项和,
证明:.
【解析】
(1)解:,当时,,
两式相减,得,所以(),又也满足,故().所以.
(2)证明:当时,,,不等式成立;
当时
.
要证,只需证,即证,
只需证,只需证,
设,则,,只需(),①
设,则,所以在上递减,,即不等式①成立.综上,数列的前项和满足.
同课章节目录
