2022-2023学年北师大版数学九年级下册第二章 二次函数 达标测试卷(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级下册第二章 二次函数 达标测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 13:39:08 | ||
图片预览




文档简介
第二章 二次函数 达标测试卷
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合要求的)
1.下列函数属于二次函数的是( )
A.y=5x+3 B.y=
C.y=2x2+x+1 D.y=
2.将二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,则下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4
3.一个小球被抛出后,距离地面的高度h (m)和飞行时间t (s)满足的函数表达式为h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1 m B.5 m
C.6 m D.7 m
4.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是( )
A.m<2 B.m>2
C.0<m≤2 D.m<-2
5.用总长为a米的材料做成如图①的矩形窗框,设窗框的宽为x米,窗框的总面积为y平方米,y关于x的函数图象如图②,当窗户透光面积最大时a的值是( )
A.9 B.8
C.6 D.不能确定
(第5题) (第6题)
6.如图,坐标系的原点为O,点P是第一象限内抛物线y=x2-1上的任意一点,PA⊥x轴于点A.则OP-PA的值为( )
A.1 B.2
C.3 D.4
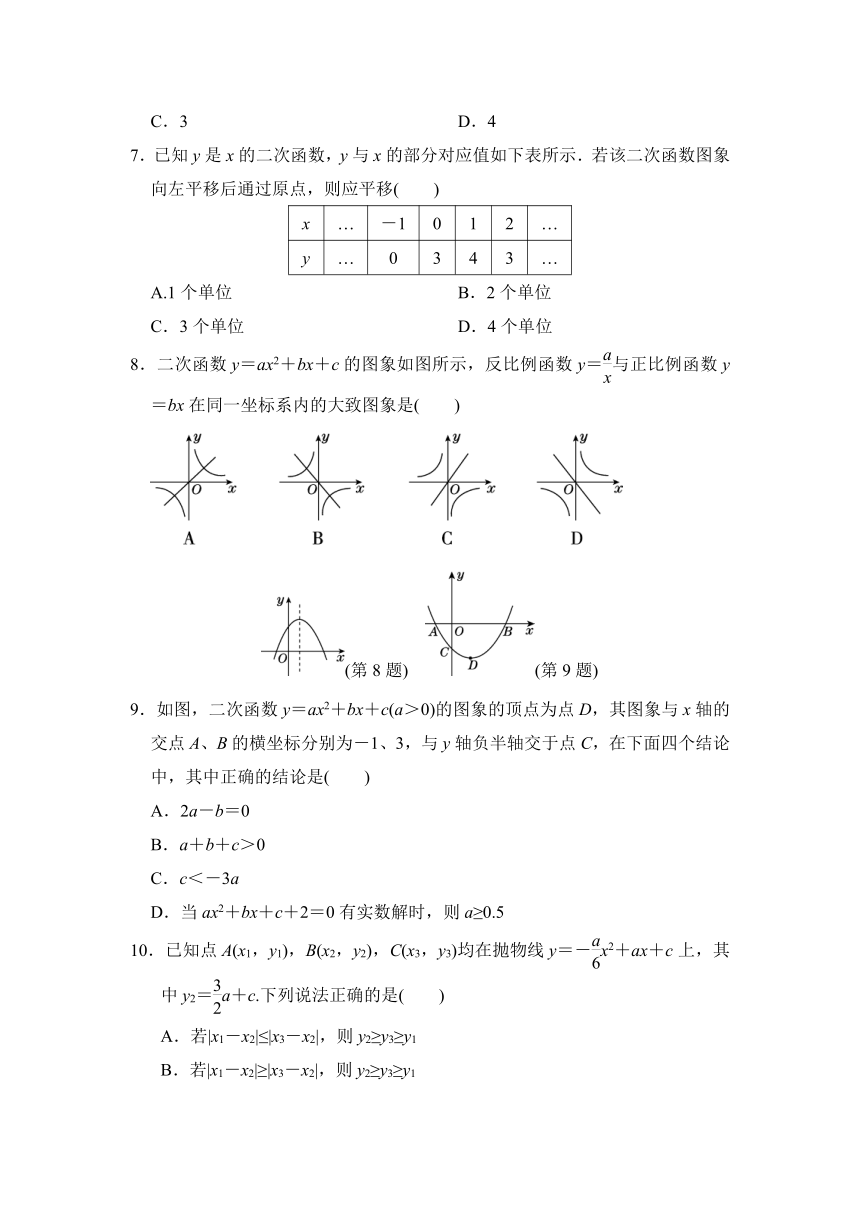
7.已知y是x的二次函数,y与x的部分对应值如下表所示.若该二次函数图象向左平移后通过原点,则应平移( )
x … -1 0 1 2 …
y … 0 3 4 3 …
A.1个单位 B.2个单位
C.3个单位 D.4个单位
8.二次函数y=ax2+bx+c的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
(第8题) (第9题)
9.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中,其中正确的结论是( )
A.2a-b=0
B.a+b+c>0
C.c<-3a
D.当ax2+bx+c+2=0有实数解时,则a≥0.5
10.已知点A(x1,y1),B(x2,y2),C(x3,y3)均在抛物线y=-x2+ax+c上,其中y2=a+c.下列说法正确的是( )
A.若|x1-x2|≤|x3-x2|,则y2≥y3≥y1
B.若|x1-x2|≥|x3-x2|,则y2≥y3≥y1
C.若y1>y3≥y2,则|x1-x2|<|x2-x3|
D.若y1>y3≥y2,则|x1-x2|>|x2-x3|
二、填空题(本题共6小题,每小题3分,共18分)
11.当a=________时,函数y=(a-1)xa2+1+x-3是二次函数.
12.请写出一个开口向上,并且与y轴交于点(0,5)的抛物线表达式________.
13.如图是二次函数y=ax2-x+a2-1的图象,则a=________.
(第13题) (第16题)
14.已知函数y=x2-2x-2,当-1≤x≤2时,y的取值范围是____________.
15.抛物线y=x2-2kx+4k经过一个定点,这个定点的坐标是____________.
16.如图,在边长为10 cm的正方形ABCD中,P为AB边上任意一点(P不与A,B两点重合),连接DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为________cm.
三、解答题(本题共6小题,共52分,解答应写出文字说明、证明过程或演算步骤)
17.(8分)已知二次函数y=x2+2x+m的图象过点A(3,0).
(1)求m的值;
(2)当x取何值时,函数值y随x的增大而增大?
18.(8分)如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的表达式;
(2)根据图象,直接写出满足kx+b≥(x-2)2+m的x的取值范围.
19.(8分)要建如图所示两个面积相同的矩形养鸡场,为了节约材料,鸡场的一边靠着原有的一面墙,墙长a=20 m,另外的边用篱笆围成,已知篱笆总长为32 m,且在BC边上开一扇宽2 m的门GH,在EF边上开一扇宽2 m的门MN.设鸡场的一边AB长为x m.
(1)若两个鸡场的总面积为S,求S与x之间的表达式,并求出x的取值范围;
(2)若两个鸡场的总面积为96 m2,求x;
(3)直接写出当两个鸡场的总面积不小于105 m2时,x的取值范围是________.
20.(8分)某商店经营一种水产品,成本为每千克40元,根据市场分析,若按每千克50元的价格销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,当销售单价定为多少元时,获得的月利润最大?最大月利润是多少?
21.(10分)如图,已知抛物线与x轴交于A(-1,0),E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线对应的函数表达式;
(2)若抛物线的顶点为D,求四边形AEDB的面积.
22.(10分)已知抛物线y=x2+bx+c经过A(-3,n)、B(2,n)两点.
(1)求b的值;
(2)当-1<x<1时,该抛物线与x轴有且只有一个公共点,求c的取值范围;
(3)若方程x2+bx+c =0的两实根x1,x2满足3≤x2-x1<9,且p=x-3x,求p的最大值.
答案
一、1.C 2.B 3.C 4.A 5.C 6.B 7.C 8.C 9.D
10.D 点拨:∵y=-x2+ax+c=-(x-3)2+a+c,
∴函数的顶点坐标为,即为点B,
∵当a>0时,-<0,抛物线开口向下,则当x越靠近3时,y的值越大,
∴当|x1-x2|≤|x3-x2|时,y2≥y1≥y3,
当|x1-x2|≥|x3-x2|时,y2≥y3≥y1.
∵当a<0时,->0,抛物线开口向上,则当x越靠近3时,y的值越小,
∴当|x1-x2|≥|x3-x2|时,y1≥y3≥y2;
当|x1-x2|≤|x3-x2|时,y3≥y1≥y2.故选项A不正确,选项B无法确定,不符合题意;
当y1>y3≥y2时,y2是最小值,此时a<0,->0,抛物线开口向上,则当x越靠近3时,y的值越小,
∴|x1-x2|>|x2-x3|,故选项D正确,符合题意.
二、11.-1 12.y=x2+5(答案不唯一) 13.1
14.-3≤y≤1 15.(2,4)
16. 点拨:设AP=x cm,BE=y cm.如图,
在正方形ABCD中,∠A=∠B=90°.
∴∠1+∠2=90°.∵PE⊥DP,∴∠2+∠3=90°.
∴∠1=∠3.∴Rt△ADP∽Rt△BPE.∴=,
即=.整理得y=-(x-5)2+(0<x<10),
∴当x=5时,y有最大值.∴BE的最大长度为 cm.
三、17.解:(1)∵二次函数y=x2+2x+m的图象过点A(3,0),∴9+6+m=0,解得m=-15.
(2)∵y=x2+2x-15=(x+1)2-16,
∴二次函数的图象的对称轴为直线x=-1.
∵1>0,∴当x>-1时,函数值y随x的增大而增大.
18.解:(1)将点A(1,0)的坐标代入y=(x-2)2+m,
得(1-2)2+m=0,解得m=-1,
∴二次函数的表达式为y=(x-2)2-1.图象的对称轴为直线x=2.令x=0,则y=3,∴点C的坐标为(0,3).
∵点C和点B关于直线x=2对称,
∴点B的坐标为(4,3).
将A(1,0),B(4,3)的坐标分别代入y=kx+b中得解得
∴一次函数的表达式为y=x-1.
(2)满足kx+b≥(x-2)2+m的x的取值范围为1≤x≤4.
19.解:(1)题中设鸡场的一边AB长为x m,则平行于墙的一边BC长为(36-3x)米,
根据题意得:S=(36-3x)x=-3x2+36x,
∵0<36-3x≤20,∴≤x<12.
(2)根据题意得:-3x2+36x=96,解得x1=4,x2=8,
∵≤x<12,∴x=8.
(3)≤x≤7 点拨:由题意得:-3x2+36x≥105,
∴5≤x≤7,∵≤x<12,∴≤x≤7.
20.解:设销售单价定为x元,获得的月利润为w元,
由题意得w=(x-40)[500-10(x-50)]=-10x2+1 400x-40 000=-10(x-70)2+9 000,
∴当x=70时,w最大=9 000.
答:当销售单价定为70元时,获得的月利润最大,最大月利润是9 000元.
21.解:(1)∵抛物线与y轴交于点B(0,3),
∴设抛物线对应的函数表达式为y=ax2+bx+3.
又∵A(-1,0),E(3,0)在抛物线上,
∴解得
∴抛物线对应的函数表达式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴点D的坐标为(1,4).过点D作DF⊥x轴于点F,
易知F(1,0),所以OF=1,DF=4.
∵E(3,0),∴EF=2,
∵A(-1,0),B(0,3),∴OA=1,OB=3.
∴S四边形AEDB=S△ABO+S梯形BOFD+S△DEF=AO·BO+(BO+DF)·OF+EF·DF=×1×3+×(3+4)×1+×2×4=9.
∴四边形AEDB的面积为9.
22.解:(1) ∵该抛物线经过A(-3,n),B(2,n)两点,
∴该抛物线的对称轴为直线x==-.
∴-=-.∴b =1.
(2) 由(1)得,该抛物线的表达式为y=x2+x+c,
∵该抛物线对称轴为直线x=-,且当-1<x<1时,
抛物线与x轴有且只有一个公共点,
①当公共点是顶点时,Δ=1-4c=0,解得c=.
②当公共点不是顶点时,即x=-1时,1-1+c≤0;
x=1时,1+1+c>0.解得-2<c≤0.
综上所述,c的取值范围是c=或-2<c≤0.
(3)由(1)知b=1.∵方程x2 + x+c=0的两实根为x1,x2,
∴抛物线y=x2+x+c与x轴交点的横坐标为x1,x2,
∴=-,∴x1+x2=-1.即x2=-1-x1.
∵3≤x2-x1<9,∴3≤(-1-x1) -x1<9.
∴-5<x1≤-2.
∴p= x-3x=x-3(-1-x1)2=-2(x1+)2+.
∵当-5<x1≤-2时,p随x1的增大而增大,
∴当x1=-2时,p取最大值,p的最大值为1.
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合要求的)
1.下列函数属于二次函数的是( )
A.y=5x+3 B.y=
C.y=2x2+x+1 D.y=
2.将二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,则下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4
3.一个小球被抛出后,距离地面的高度h (m)和飞行时间t (s)满足的函数表达式为h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1 m B.5 m
C.6 m D.7 m
4.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是( )
A.m<2 B.m>2
C.0<m≤2 D.m<-2
5.用总长为a米的材料做成如图①的矩形窗框,设窗框的宽为x米,窗框的总面积为y平方米,y关于x的函数图象如图②,当窗户透光面积最大时a的值是( )
A.9 B.8
C.6 D.不能确定
(第5题) (第6题)
6.如图,坐标系的原点为O,点P是第一象限内抛物线y=x2-1上的任意一点,PA⊥x轴于点A.则OP-PA的值为( )
A.1 B.2
C.3 D.4
7.已知y是x的二次函数,y与x的部分对应值如下表所示.若该二次函数图象向左平移后通过原点,则应平移( )
x … -1 0 1 2 …
y … 0 3 4 3 …
A.1个单位 B.2个单位
C.3个单位 D.4个单位
8.二次函数y=ax2+bx+c的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
(第8题) (第9题)
9.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中,其中正确的结论是( )
A.2a-b=0
B.a+b+c>0
C.c<-3a
D.当ax2+bx+c+2=0有实数解时,则a≥0.5
10.已知点A(x1,y1),B(x2,y2),C(x3,y3)均在抛物线y=-x2+ax+c上,其中y2=a+c.下列说法正确的是( )
A.若|x1-x2|≤|x3-x2|,则y2≥y3≥y1
B.若|x1-x2|≥|x3-x2|,则y2≥y3≥y1
C.若y1>y3≥y2,则|x1-x2|<|x2-x3|
D.若y1>y3≥y2,则|x1-x2|>|x2-x3|
二、填空题(本题共6小题,每小题3分,共18分)
11.当a=________时,函数y=(a-1)xa2+1+x-3是二次函数.
12.请写出一个开口向上,并且与y轴交于点(0,5)的抛物线表达式________.
13.如图是二次函数y=ax2-x+a2-1的图象,则a=________.
(第13题) (第16题)
14.已知函数y=x2-2x-2,当-1≤x≤2时,y的取值范围是____________.
15.抛物线y=x2-2kx+4k经过一个定点,这个定点的坐标是____________.
16.如图,在边长为10 cm的正方形ABCD中,P为AB边上任意一点(P不与A,B两点重合),连接DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为________cm.
三、解答题(本题共6小题,共52分,解答应写出文字说明、证明过程或演算步骤)
17.(8分)已知二次函数y=x2+2x+m的图象过点A(3,0).
(1)求m的值;
(2)当x取何值时,函数值y随x的增大而增大?
18.(8分)如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的表达式;
(2)根据图象,直接写出满足kx+b≥(x-2)2+m的x的取值范围.
19.(8分)要建如图所示两个面积相同的矩形养鸡场,为了节约材料,鸡场的一边靠着原有的一面墙,墙长a=20 m,另外的边用篱笆围成,已知篱笆总长为32 m,且在BC边上开一扇宽2 m的门GH,在EF边上开一扇宽2 m的门MN.设鸡场的一边AB长为x m.
(1)若两个鸡场的总面积为S,求S与x之间的表达式,并求出x的取值范围;
(2)若两个鸡场的总面积为96 m2,求x;
(3)直接写出当两个鸡场的总面积不小于105 m2时,x的取值范围是________.
20.(8分)某商店经营一种水产品,成本为每千克40元,根据市场分析,若按每千克50元的价格销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,当销售单价定为多少元时,获得的月利润最大?最大月利润是多少?
21.(10分)如图,已知抛物线与x轴交于A(-1,0),E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线对应的函数表达式;
(2)若抛物线的顶点为D,求四边形AEDB的面积.
22.(10分)已知抛物线y=x2+bx+c经过A(-3,n)、B(2,n)两点.
(1)求b的值;
(2)当-1<x<1时,该抛物线与x轴有且只有一个公共点,求c的取值范围;
(3)若方程x2+bx+c =0的两实根x1,x2满足3≤x2-x1<9,且p=x-3x,求p的最大值.
答案
一、1.C 2.B 3.C 4.A 5.C 6.B 7.C 8.C 9.D
10.D 点拨:∵y=-x2+ax+c=-(x-3)2+a+c,
∴函数的顶点坐标为,即为点B,
∵当a>0时,-<0,抛物线开口向下,则当x越靠近3时,y的值越大,
∴当|x1-x2|≤|x3-x2|时,y2≥y1≥y3,
当|x1-x2|≥|x3-x2|时,y2≥y3≥y1.
∵当a<0时,->0,抛物线开口向上,则当x越靠近3时,y的值越小,
∴当|x1-x2|≥|x3-x2|时,y1≥y3≥y2;
当|x1-x2|≤|x3-x2|时,y3≥y1≥y2.故选项A不正确,选项B无法确定,不符合题意;
当y1>y3≥y2时,y2是最小值,此时a<0,->0,抛物线开口向上,则当x越靠近3时,y的值越小,
∴|x1-x2|>|x2-x3|,故选项D正确,符合题意.
二、11.-1 12.y=x2+5(答案不唯一) 13.1
14.-3≤y≤1 15.(2,4)
16. 点拨:设AP=x cm,BE=y cm.如图,
在正方形ABCD中,∠A=∠B=90°.
∴∠1+∠2=90°.∵PE⊥DP,∴∠2+∠3=90°.
∴∠1=∠3.∴Rt△ADP∽Rt△BPE.∴=,
即=.整理得y=-(x-5)2+(0<x<10),
∴当x=5时,y有最大值.∴BE的最大长度为 cm.
三、17.解:(1)∵二次函数y=x2+2x+m的图象过点A(3,0),∴9+6+m=0,解得m=-15.
(2)∵y=x2+2x-15=(x+1)2-16,
∴二次函数的图象的对称轴为直线x=-1.
∵1>0,∴当x>-1时,函数值y随x的增大而增大.
18.解:(1)将点A(1,0)的坐标代入y=(x-2)2+m,
得(1-2)2+m=0,解得m=-1,
∴二次函数的表达式为y=(x-2)2-1.图象的对称轴为直线x=2.令x=0,则y=3,∴点C的坐标为(0,3).
∵点C和点B关于直线x=2对称,
∴点B的坐标为(4,3).
将A(1,0),B(4,3)的坐标分别代入y=kx+b中得解得
∴一次函数的表达式为y=x-1.
(2)满足kx+b≥(x-2)2+m的x的取值范围为1≤x≤4.
19.解:(1)题中设鸡场的一边AB长为x m,则平行于墙的一边BC长为(36-3x)米,
根据题意得:S=(36-3x)x=-3x2+36x,
∵0<36-3x≤20,∴≤x<12.
(2)根据题意得:-3x2+36x=96,解得x1=4,x2=8,
∵≤x<12,∴x=8.
(3)≤x≤7 点拨:由题意得:-3x2+36x≥105,
∴5≤x≤7,∵≤x<12,∴≤x≤7.
20.解:设销售单价定为x元,获得的月利润为w元,
由题意得w=(x-40)[500-10(x-50)]=-10x2+1 400x-40 000=-10(x-70)2+9 000,
∴当x=70时,w最大=9 000.
答:当销售单价定为70元时,获得的月利润最大,最大月利润是9 000元.
21.解:(1)∵抛物线与y轴交于点B(0,3),
∴设抛物线对应的函数表达式为y=ax2+bx+3.
又∵A(-1,0),E(3,0)在抛物线上,
∴解得
∴抛物线对应的函数表达式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴点D的坐标为(1,4).过点D作DF⊥x轴于点F,
易知F(1,0),所以OF=1,DF=4.
∵E(3,0),∴EF=2,
∵A(-1,0),B(0,3),∴OA=1,OB=3.
∴S四边形AEDB=S△ABO+S梯形BOFD+S△DEF=AO·BO+(BO+DF)·OF+EF·DF=×1×3+×(3+4)×1+×2×4=9.
∴四边形AEDB的面积为9.
22.解:(1) ∵该抛物线经过A(-3,n),B(2,n)两点,
∴该抛物线的对称轴为直线x==-.
∴-=-.∴b =1.
(2) 由(1)得,该抛物线的表达式为y=x2+x+c,
∵该抛物线对称轴为直线x=-,且当-1<x<1时,
抛物线与x轴有且只有一个公共点,
①当公共点是顶点时,Δ=1-4c=0,解得c=.
②当公共点不是顶点时,即x=-1时,1-1+c≤0;
x=1时,1+1+c>0.解得-2<c≤0.
综上所述,c的取值范围是c=或-2<c≤0.
(3)由(1)知b=1.∵方程x2 + x+c=0的两实根为x1,x2,
∴抛物线y=x2+x+c与x轴交点的横坐标为x1,x2,
∴=-,∴x1+x2=-1.即x2=-1-x1.
∵3≤x2-x1<9,∴3≤(-1-x1) -x1<9.
∴-5<x1≤-2.
∴p= x-3x=x-3(-1-x1)2=-2(x1+)2+.
∵当-5<x1≤-2时,p随x1的增大而增大,
∴当x1=-2时,p取最大值,p的最大值为1.
