二轮专题复习:专题八 第二讲 数形结合思想(共36张PPT)
文档属性
| 名称 | 二轮专题复习:专题八 第二讲 数形结合思想(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 00:50:22 | ||
图片预览











文档简介
(共36张PPT)
专题八 思想方法专题
第二讲 数形结合思想
以数助形与以形助数
数形结合的数学思想包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.
代数问题几何化与几何问题代数化
数形结合思想的实质、关键及运用时应注意的问题:其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.在运用数形结合思想分析和解决问题时,要注意三点:第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二是恰当设参,合理用参,建立关系,由数思形,以形思数,做好数形转化;第三是正确确定参数的取值范围.
数形结合解决广泛的数学问题
数形结合思想解决的相关问题.
数形结合思想应用广泛,高考试题对数形结合的考查主要涉及:
(1)考查集合及其运算问题(韦恩图与数轴).
(2)考查用函数图象解决有关问题(如方程、不等式、函数的有关性质等).
(3)考查运用向量解决有关问题.
(4)考查三角函数的图象及其应用.
(5)解析几何、立体几何中的数形结合.
1.函数y=log2 的图象( )
A.关于原点对称 B.关于直线y=-x对称
C.关于轴对称 D.关于直线y=x对称
解析:本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又f(-x)=-f(x),故函数为奇函数,图象关于原点对称,选A.
答案:A
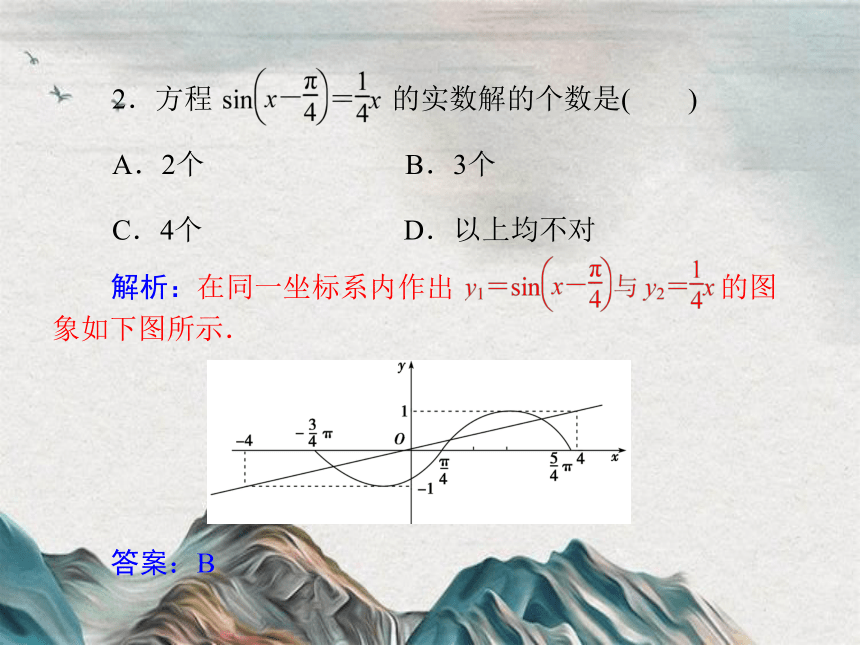
2.方程 的实数解的个数是( )
A.2个 B.3个
C.4个 D.以上均不对
解析:在同一坐标系内作出 的图象如下图所示.
答案:B
3.设集合A,B是全集U的两个子集,则A? B是( UA)∪B=U的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:如图,
A ?B时,有( UA)∪B=U;
A=B时,有( UA)∪B=U成立.
综合以上情形,可得A ?B ( UA)∪B=U,但( UA)∪B=UD A B.
答案:A
/
4.(2012年天津卷)已知函数y= 的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范围是________.
解析:解法一:
解法二:
作出函数的图象,要使函数y与y=kx-2有两个不同的交点,则直线y=kx-2必须在四边形区域ABCD内(和直线y=x+1平行的直线除外),如图,则此时直线经过B(1,2),k= =4.
综上所述,k的取值范围是0答案:(0,1)∪(1,4)
突破点1 用数形结合思想解决方程、不等式及函数的有关性质问题
(1)已知:函数f(x)满足下面关系:①f(x+1)= f(x-1);②当x∈[-1,1]时,f(x)=x2,则方程f(x)=lg x解的个数是( )
A.5个 B.7个 C.9个 D.10个
解析:(1)由题意可知,f(x)是以2为周期,值域为[0,1]的函数.又f(x)=lgx,则x∈(0,10],画出两函数图象,则交点个数即为解的个数.
由图象可知共9个交点.
误区警示:作图时弄清y=lg x的图象何时超过1,否则易造成结果错误.
规律方法:(1)用函数的图象讨论方程(特别是含参数的指数、对数、根式、三角等复杂方程)的解的个数是一种重要的思想方法,其基本思想是先把方程两边的代数式看作是两个熟悉函数的表达式(不熟悉时,需要作适当变形转化为两熟悉的函数),然后在同一坐标系中作出两个函数的图象,图象的交点个数即为方程解的个数.(2)解不等式问题经常联系函数的图象,根据不等式中量的特点,选择适当的两个(或多个)函数,利用两个函数图象的上、下位置关系转化数量关系来解决不等式的解的问题,往往可以避免繁琐的运算,获得简捷的解答. (3)函数的单调性经常联系函数图象的升、降;奇偶性经常联系函数图象的对称性;最值(值域)经常联系函数图象的最高、最低点的纵坐标.
跟踪训练
1.已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
解析:因为定义在R上的奇函数,满足f(x-4)=-f(x),所以f(x-4)=f(-x),由f(x)为奇函数,所以函数图象关于直线x=2对称且f(0)=0.由f(x-4)=-f(x)知f(x-8)=f(x),所以函数是以8为周期的周期函数,又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,不妨设x1<x2<x3<x4由对称性知x1+x2=-12,x3+x4=4所以x1+x2+x3+x4=-12+4=-8.
答案:-8
突破点2 用数形结合解决参数、代数式的最值、取值范围问题
思路点拨:(1)此题令b=y-3x,即y=3x+b,视b为直线y=3x+b的截距,而直线与椭圆必有公共点,故相切时,b有最值.
(2)此题可转化成过点(-1,-3)与不等式组 表示区域的点的连线的斜率的范围.
得169x2+96bx+16b2-400=0,
令Δ=0,解得b=±13.
故y-3x的最大值为13,最小值为-13.
(2)由解析几何知识可知,所给的不等式组表示圆x2+y2=4的右半圆域(含边界),
误区警示:此题很容易犯的错误是由z= 得到点 (-1,-3)的坐标时,很容易写成(1,3),所以做题时要看清顺序.
规律方法:如果参数、代数式的结构蕴含着明显的几何特征,一般考虑用数形结合的方法来解题,即所谓的几何法求解,比较常见的对应有:
(1)y=kx+b中k表示直线的斜率,b表示直线在y轴上的截距.
跟踪训练
2.若例题2(1)中条件不变,求5x+4y的最大值与最小值.
突破点3 数形结合思想在几何中的应用
规律方法:(1)本题考查抛物线的性质、三点共线的坐标关系和综合运算的能力,属于中档难度题.
(2)先由图象特点,将面积之比转化为线段长度之比,再利用抛物线的定义和三点共线(即斜率)解决,体现了数形结合思想.
跟踪训练
3.在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p>0)相交于点A,B.
(1)若点N是点C关于坐标原点O的对称点,求△ANB面积的最小值.
(2)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,请说明理由.
解析:(1)如图所示,依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2).
直线AB的方程为y=kx+p与x2=2py联立,消去y,得x2-2pkx-2p2=0.
由根与系数的关系,得x1+x2=2pk,x1x2=-2p2.
(2)如图所示,假设满足条件的直线l存在,其方程为y=a.
设AC的中点为点O′,l与以AC为直径的圆相交于点P,Q,PQ的中点为点H.
1.数形结合是解决许多数学问题的重要方法,它可以将抽象数学问题具体化、准确化、形象化.我们用好数形结合可以使我们更深入准确的理解数学问题.
2.数形结合主要应用于:函数、三角、集合、立几、解几、向量、不等式等.
3.是否选择应用数形结合的原则是:是否有利于解决问题,用最简单的办法解决问题为最终目的.
专题八 思想方法专题
第二讲 数形结合思想
以数助形与以形助数
数形结合的数学思想包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质.
代数问题几何化与几何问题代数化
数形结合思想的实质、关键及运用时应注意的问题:其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.在运用数形结合思想分析和解决问题时,要注意三点:第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二是恰当设参,合理用参,建立关系,由数思形,以形思数,做好数形转化;第三是正确确定参数的取值范围.
数形结合解决广泛的数学问题
数形结合思想解决的相关问题.
数形结合思想应用广泛,高考试题对数形结合的考查主要涉及:
(1)考查集合及其运算问题(韦恩图与数轴).
(2)考查用函数图象解决有关问题(如方程、不等式、函数的有关性质等).
(3)考查运用向量解决有关问题.
(4)考查三角函数的图象及其应用.
(5)解析几何、立体几何中的数形结合.
1.函数y=log2 的图象( )
A.关于原点对称 B.关于直线y=-x对称
C.关于轴对称 D.关于直线y=x对称
解析:本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又f(-x)=-f(x),故函数为奇函数,图象关于原点对称,选A.
答案:A
2.方程 的实数解的个数是( )
A.2个 B.3个
C.4个 D.以上均不对
解析:在同一坐标系内作出 的图象如下图所示.
答案:B
3.设集合A,B是全集U的两个子集,则A? B是( UA)∪B=U的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:如图,
A ?B时,有( UA)∪B=U;
A=B时,有( UA)∪B=U成立.
综合以上情形,可得A ?B ( UA)∪B=U,但( UA)∪B=UD A B.
答案:A
/
4.(2012年天津卷)已知函数y= 的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范围是________.
解析:解法一:
解法二:
作出函数的图象,要使函数y与y=kx-2有两个不同的交点,则直线y=kx-2必须在四边形区域ABCD内(和直线y=x+1平行的直线除外),如图,则此时直线经过B(1,2),k= =4.
综上所述,k的取值范围是0
突破点1 用数形结合思想解决方程、不等式及函数的有关性质问题
(1)已知:函数f(x)满足下面关系:①f(x+1)= f(x-1);②当x∈[-1,1]时,f(x)=x2,则方程f(x)=lg x解的个数是( )
A.5个 B.7个 C.9个 D.10个
解析:(1)由题意可知,f(x)是以2为周期,值域为[0,1]的函数.又f(x)=lgx,则x∈(0,10],画出两函数图象,则交点个数即为解的个数.
由图象可知共9个交点.
误区警示:作图时弄清y=lg x的图象何时超过1,否则易造成结果错误.
规律方法:(1)用函数的图象讨论方程(特别是含参数的指数、对数、根式、三角等复杂方程)的解的个数是一种重要的思想方法,其基本思想是先把方程两边的代数式看作是两个熟悉函数的表达式(不熟悉时,需要作适当变形转化为两熟悉的函数),然后在同一坐标系中作出两个函数的图象,图象的交点个数即为方程解的个数.(2)解不等式问题经常联系函数的图象,根据不等式中量的特点,选择适当的两个(或多个)函数,利用两个函数图象的上、下位置关系转化数量关系来解决不等式的解的问题,往往可以避免繁琐的运算,获得简捷的解答. (3)函数的单调性经常联系函数图象的升、降;奇偶性经常联系函数图象的对称性;最值(值域)经常联系函数图象的最高、最低点的纵坐标.
跟踪训练
1.已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
解析:因为定义在R上的奇函数,满足f(x-4)=-f(x),所以f(x-4)=f(-x),由f(x)为奇函数,所以函数图象关于直线x=2对称且f(0)=0.由f(x-4)=-f(x)知f(x-8)=f(x),所以函数是以8为周期的周期函数,又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,不妨设x1<x2<x3<x4由对称性知x1+x2=-12,x3+x4=4所以x1+x2+x3+x4=-12+4=-8.
答案:-8
突破点2 用数形结合解决参数、代数式的最值、取值范围问题
思路点拨:(1)此题令b=y-3x,即y=3x+b,视b为直线y=3x+b的截距,而直线与椭圆必有公共点,故相切时,b有最值.
(2)此题可转化成过点(-1,-3)与不等式组 表示区域的点的连线的斜率的范围.
得169x2+96bx+16b2-400=0,
令Δ=0,解得b=±13.
故y-3x的最大值为13,最小值为-13.
(2)由解析几何知识可知,所给的不等式组表示圆x2+y2=4的右半圆域(含边界),
误区警示:此题很容易犯的错误是由z= 得到点 (-1,-3)的坐标时,很容易写成(1,3),所以做题时要看清顺序.
规律方法:如果参数、代数式的结构蕴含着明显的几何特征,一般考虑用数形结合的方法来解题,即所谓的几何法求解,比较常见的对应有:
(1)y=kx+b中k表示直线的斜率,b表示直线在y轴上的截距.
跟踪训练
2.若例题2(1)中条件不变,求5x+4y的最大值与最小值.
突破点3 数形结合思想在几何中的应用
规律方法:(1)本题考查抛物线的性质、三点共线的坐标关系和综合运算的能力,属于中档难度题.
(2)先由图象特点,将面积之比转化为线段长度之比,再利用抛物线的定义和三点共线(即斜率)解决,体现了数形结合思想.
跟踪训练
3.在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p>0)相交于点A,B.
(1)若点N是点C关于坐标原点O的对称点,求△ANB面积的最小值.
(2)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,请说明理由.
解析:(1)如图所示,依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2).
直线AB的方程为y=kx+p与x2=2py联立,消去y,得x2-2pkx-2p2=0.
由根与系数的关系,得x1+x2=2pk,x1x2=-2p2.
(2)如图所示,假设满足条件的直线l存在,其方程为y=a.
设AC的中点为点O′,l与以AC为直径的圆相交于点P,Q,PQ的中点为点H.
1.数形结合是解决许多数学问题的重要方法,它可以将抽象数学问题具体化、准确化、形象化.我们用好数形结合可以使我们更深入准确的理解数学问题.
2.数形结合主要应用于:函数、三角、集合、立几、解几、向量、不等式等.
3.是否选择应用数形结合的原则是:是否有利于解决问题,用最简单的办法解决问题为最终目的.
同课章节目录
